Abstract
Backtracking is a standard-method to find solutions for particular kind of problems, known as "Constraint-Satisfaction"-Problems. These Problems define a set of Constraints to validate any tryal. The most primitive way to solve them is "Brute-Force" - that means: Simply try everything out ;-)
Now Backtracking is applicable (and is an exorbitant improvement), if you can build the tryals stepwise. Then you can check the rules each step, and on failure you can skip all further steps in that direction.
Note: Eg on Path-Finding-Problems Backtracking is possible, but not efficient. Better use a FloodFill-Derivate, Dijkstra or something else.
Even the Knights-Tour-Puzzle, or the Frog-Hopping can be done very much better by respecting additional heuristics.
The eight Queens Problem
is a nice sample-puzzle, where Backtracking is applicable and efficient - it is defined as:
"Find all ways, to place eigth queens on a chessboard, each occupying 1) her own row 2) her own column 3) her own ascending diagonale 4) her own descending diagonale"
My QueenProblems Problem
To me the most difficult was, to change my way of viewing a chessboard: In a backtrackings point of view it's not a 2-dimensioned matrix, but is a tree-structure with depth of eight, and each node has eight childnodes.
Or let me try in other words: On 8-Q-Problem the Backtracking uses no nested x-/y-iteration. Instead of that it steps forward the rows one by one, and on each row it examines, with which of the eight columns it can continue. It steps (row-)backwards, if there is no valid column in that row, (where the queen could be placed).
This way of view is crucial from the very beginning: The first of the four constraints mentioned above can be removed, since the stepping from row to row implies that a row-conflict never can occur.
A "mathematical discovery" ;-)
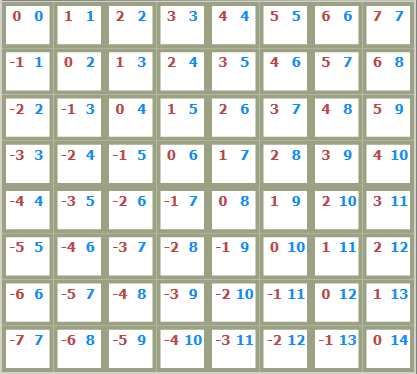
while thinking about an efficiant way to check the remaining three rules, i've got the idea of 3 hashsets, which stores kind of Identifiers about the already occupied 1) colum 2) asc diagonale 3) desc diagonale.
1) is trivial, since columns are numbered.
2) also wellknown (to me): In a two-dimensional matrix on descending diagonales the x-y-Difference is constant.
3) (you can't imagine, how hard i thought about it, to figure out that simple truth): on ascending diagonales the x-y-Sum is constant.
To make clear what i mean, i created an Image (red numbs: x-y, blue numbs: x+y):
Code
Constraint-Validation-Mechanism
You see: simpliest Maths gives way to derive from any chess-field the "constraint-Id" in each of the 3 (remaining) "Dimensions": 1) column 2) ascending diagonale 3) descending diagonale.
A Hashset<int> is the perfect storage for those Constraint-Ids, since its Add()-Method rejects adding an Id twice. Moreover on rejecting the Method returns false.
private static HashSet<int>[] _Occupieds = Enumerable.Range(0, 3).Select(i => new HashSet<int>()).ToArray();
private static Func<int, int, int>[] _GetOccupyIds = new Func<int, int, int>[] {
(x, y) => x,
(x, y) => x + y,
(x, y) => x - y };
private static bool Occupy(int col, int row) {
int[] tempIds = new int[3];
for (var i = 3; i-- > 0; ) {
tempIds[i] = _GetOccupyIds[i](col, row);
if (!_Occupieds[i].Add(tempIds[i])) {
while (++i < 3) _Occupieds[i].Remove(tempIds[i]);
return false;
}
}
return true;
}
private static void DeOccupy(int col, int row) {
for (var i = 3; i-- > 0; ) _Occupieds[i].Remove(_GetOccupyIds[i](col, row));
}
There are 3 HashSets, and 3 Func<int, int> - Delegates.
When trying to "put a queen on chessboard" the method Occupy() uses the Delegates to calculate the "Id" of each "dimension" (column, asc diagonale, desc diagonale).
Then try to add it to the corresponding Hashset. If that fails remove the possibly previous added Ids of the other "dimensions", before exit and return false.
The other method - DeOccupy() is needed to remove previous stored Constraint-Ids when Backtracking steps back ("remove a Queen from board").
Search-Algorithm
public static List<int[]> FindAll() {
var queens = new Stack<int>();
var output = new List<int[]>();
Action recurse = null;
recurse = () => {
var row = queens.Count;
if (row == _BoardSize) {
output.Add(queens.ToArray());
return;
}
for (var col = 0; col < _BoardSize; col++) {
if (Occupy(col, row)) {
queens.Push(col);
recurse();
queens.Pop();
DeOccupy(col, row);
}
}
};
recurse();
return output;
}
As mentioned in the Abstract, Backtracking builds its tryals step by step. That means to the 8-Q-Problem: row by row. And each step occupies a specific column (in which the queen is placed - for that row).
Long story short: The integers in the queens-Stack are the complete Representation of the current tryal and its state of progress.
Note one of my favourites - the local recursion:
The whole algorithm finds place in the shown method, and the recursive part is done by an anonymous method in a local variable, namely named "recurse" ;-)
So i can hold the queens-Stack, and the output-List as local variables - there is neither a need to design them as class-var, nor to pass them as parameter through all the recursive calls, which will occur.
Lets examine more deeply, what the anonyme recursive method does:
var row = queens.Count;
As said the stack-count is identical to the current tryals progress-state, and also is identical to the row in examination.
Accordingly the next 3 lines check if and react when the tryals state is "complete".
Otherwise check each column, and if you find a position which you can occupy successfully, note it on Stack and recurse.
After recursing comes the backtracking of the Backtracking-Algorithm: Denote the tryal-step from stack and also de-occupy its constraint-Ids.
You see: An absolutely usually recursive method.
Output
As seen, FindAll() returns the solutions as List<int[]>. Lets see, how to translate an int[] to a string a chess-player would understand, namely to the "A1" - Format:
static void Main(string[] args) {
Func<int[], string> getA1addresses = columnList => string.Concat(columnList.Select((col, i) => " " + (char)('a' + col) + (i + 1)));
List<int[]> columnLists = Find8Queens.FindAll();
Console.WriteLine(string.Join("\n", columnLists.Select(getA1addresses)));
Console.WriteLine(columnLists.Count.ToString() + " Results");
Console.Read();
}
The first line does the job:
Func<int[], string> getA1addresses =
columnList => string.Concat(columnList.Select((col, i) => " " + (char)('a' + col) + (i + 1)));
Get the Letter by adding the column col to 'a'
The list-index i is the row, but zero-based. So add 1 to it to get the digit according to the "A1"-format.
Append the above to " " and you have the "A1"-formatted Display of one entry of the columnList.
Concatenize all the eight entries, and the result-string tells, what the chess-player needs to know: where to place the queens ;-)
A second one: doing the same, but very different
Credits to codeproject-member djmarcus - he posted a comment and gave a completely different concept of validating the 8-Queens-Rules - including the code to achieve it.
If you like, refer to his comment in the discussion-section of this article.
Validation-concept II
djmarcus pointed out, that all squares of a chessboard can be represented simply as bits within a single uint64. This gives the opportunity to create an "attack-Vector" for each position a queen can occupy - as said - whithin one number. Now with simple Bit-Operation And you can check wether a position "is under attack". Moreover with simple Inclusive Or-Operation you can cumulative add several attackVectors as well as you can cumulate several queen-positions, (when several queens succesfully are placed on the board).
Code II
I only show the recursive solve()-function - since it's the main-part, and most convincing, while the attackVectors preparation is more line-expensive:
private bool solve(int row, ulong queens, ulong attacks) {
if (row == 8) { displayVector("Solution:", queens); return foundSolution; }
for (var col = 0; col < 8; col++) {
ulong positionVector = _positionVectors[row * 8 + col];
if ((attacks & positionVector) == 0) {
if (solve(row + 1, queens | positionVector, attacks | _attackVectors[row * 8 + col]))
return foundSolution;
}
}
return false;
}
if (row == 8) { displayVector("Solution:", queens); return foundSolution; }
Again at first is checked, whether the row-maxSize is reached, that indicates a found solution and leads to output and exit function.
ulong positionVector = _positionVectors[row * 8 + col];
(not yet mentioned: ) also a "positionVectors"-Array is prepared, so that to each row/column - defined position its represantation as ulong is available.
if ((attacks & positionVector) == 0) {
This one is the check, whether the current position conflicts with any attack(-bit).
if (solve(row + 1, queens | positionVector, attacks | _attackVectors[row * 8 + col])) return foundSolution;
On no conflict (which was checked the line before) the recursion takes a step forward. The tryal-progress of this step-forward is represented by the three modifications of the parameters, passed to the self-call:
- increment the row:
row + 1 - cumulative add the successfull new position:
queens | positionVector - cumulative add the associated attackVector:
attacks | _attackVectors[row * 8 + col]
This models exactly, what happens, when a chess-player puts the next Queen on an available column of the next row: 1) he enters the next row, 2) one more queen is present, 3) one more group of attacked squares is to respect.
As said: For brevity i do not present the Preparation-Code of attack- and position-Vectors. But nevertheless even that preparations are cruicial for the performance: On each tryal there is nothing to compute - instead of that the prepared result can simply be taken from an Array.
Keep this in mind: Storing prepared results, instead of computing them each time is a highly effective technique to optimize algorithms for speed.
Output II
Even the Output is very different. While i compose a line with "A1"-formatted Positions, the output of djmarcus creates a kind of "Ascii-Art" - compare:
a1 e2 h3 f4 c5 g6 b7 d8
|
Q * * * * * * *
* * * * Q * * *
* * * * * * * Q
* * * * * Q * *
* * Q * * * * *
* * * * * * Q *
* Q * * * * * *
* * * Q * * * *
|
djmarcus' output-code, using two nested for-loops:
for(int row = 0; row < 8; row++) {
Console.WriteLine();
for (int col = 0; col < 8; col++) Console.Write((
queens & _positionVectors[row * 8 + col]) != 0 ? " Q " : " * ");
}
Points of Interest
To me the "mathematical discovery" was the most important thing i learned. Eg now i see alternative ways to define the two Dimensions of a 2-D-matrix (and even to address elements) than columns and rows.
I mean: the field (2, 4) - addressed by asc/desc Diagonales it would come up as: (6, -2)
(check it, against the picture above :-) )
Maybe to you the "local-recursion"-trick is the fanciest - since it is quite unknown, although its advantages in many cases.
Lately I am very happy to be able to present as second, very different approach, and both do the same, namely solve the 8-Q-Problem by Backtracking.
Note, that on my approach, i have explicit step-back-Actions: pop the failing queen from the tryal-stack, remove her "occupy-ids" from hashsets - these things djmarcus is rid off, since he can pass the complete tryal-state - all queens, all attacked squares - within 2 single numbers to the recursive call. So the return from recursion is step-back enough, and he can continue straight on with the state, which was present before entering the recursion.
There could be said much more, comparing both approaches and search pros and cons. My point is, also to look at the commons, which makes the main-principle emerge very clearly, i think.
Conclusion
We saw Backtracking as method to solve "Constraint-Satisfaction-Problems", and applicable, when a tryal can be developed step by step. The Principle is, to discard a tryal as soon as it becomes invalid, and return to a previous state, where the tryal was less developed, but still valid, and continue developing it another way.
EG on eight-Queens-Problem all further tryals can be skipped, when already in the first two rows two queens attack each other.
Mostly this stepping back to a previous state is achieved by Recursion, and so was here, in both samples.
In Fact Backtracking also can be seen as Organizing the problem as decision-tree and performe a depth-first-traversal through it, skipping all those branches, who are not worth-while.
(Note: Like any depth-first-traversal Backtracking can also be done by non-recursive implementations, (but in this article is not.))
