This article discusses an HTML application to visualize the sum of the first ten harmonics, in 2D and 3D, and also play the sound corresponding to this sum.
1. Introduction
The code also available at https://github.com/amarnaths0005/SineSum2
You can use this online at SineSum2.
In undergraduate courses on Electrical Engineering, students come across the problem of finding the sum of sine values. While some students find it easy to understand the concept, a few others find it not as easy. SineSum is a program which helps a student to understand the sum of sines by means of visual aids to view the sum, and seeing how things change when the different amplitudes and phases are varied.
One of the courses which has attracted me is the Fourier Transform course available on Stanford Engineering Everywhere. In the very second lesson, the Professor introduces the SineSum program, which is a Matlab program to visualize the sum of sines. I recently embarked on a journey of learning the HTML5 technologies (HTML, CSS and Javascript), and thought it a good idea to rewrite the Matlab-based SineSum program in HTML5, so that it can run on the browser. This application is a result of that journey into HTML5.
2. Sum of Sines
When many sine-based expressions of different amplitudes and phases are added together (aka superposed), the result is a sum of sines. Since the sine values range from -A to +A for an amplitude value of A, superposing two sine values is not akin to mere addition of their amplitudes. The amplitudes, phases and frequencies assemble together in a not-so-straightforward manner to give the resulting sum. It is precisely this sum of sines that this application enables one to visualize. The sum of sines is defined as the sum
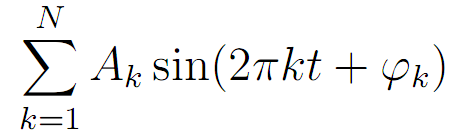
where Ak are the different amplitudes and φk are the different phases. The individual components are called harmonics; for example, the constituent involving A3 and φ3 constitutes the third harmonic. The total number of harmonics in this sum is N, and t is time variable. In our case, N is 10, and the sum, expressed more explicitly, is:

In other words, this HTML5 application calculates the sum of the first ten harmonics, allowing the user to vary the individual amplitudes and phases. The user can visualize the profile of an individual harmonic, and also the sum of the sines. A spectral profile, in 3D, is also shown. A screenshot of the application, on Chrome, is given below.

At the top of the screen, the user selects the harmonic number for which (s)he needs to specify the amplitude and phase, and varies that amplitude and phase using the slider controls at the top. As these amplitude and phase values are modified, the corresponding row in the table gets modified accordingly, and the three graphs below get dynamically changed. The Spectral Profile graph shows these amplitude and phase values as a 3D plot. The waveform of the harmonic being currently modified is shown in the middle graph below the table. The right-most graph below the table shows the sum of sines, the result of superposition of the ten harmonics. Clicking on the Play Sound button at the top plays the sound corresponding to current set of amplitudes and phases.
In the rest of the article, we describe the software aspects for achieving this result.
3. Requirements in Greater Detail
In this part of the article, the requirements are presented in more detail. The following figure lists the IDs of the GUI elements, in the HTML, and the software requirements are presented in the table after the figure.

| User Action | Application Functionality |
User changes the Harmonic Number on the opHarmonic option box. |
- Range Sliders
raAmpl and raPhase should reflect the amplitude and phase values corresponding to the chosen harmonic. The output fields, opAmpl and opPhase should also reflect these values. - Table
tblHarmonic should highlight the row corresponding to the current harmonic with a different colour. - The
canvas01 should change to show the waveform corresponding to the current harmonic.
|
| User changes the value in the range slider raAmpl. |
- The output field
opAmpl should change accordingly. - In the table
tblHarmonic, the amplitude corresponding to the current harmonic should change accordingly. - The amplitude displayed in
canvas01 should change dynamically. Canvas canvas02, displaying the sum of sines should change dynamically.- In the
canvas canvas03 showing the 3D Spectral profile, the amplitude line for the current harmonic should change dynamically.
|
User changes the value in the range slider raPhase. |
- Similar to the above (the case of
raAmpl), but with respect to phase.
|
User clicks on a row of the table tblHarmonic. |
- The clicked row should highlight in a different colour.
- The option box
opHarmonic should change to the current harmonic value. - The UI elements
raAmpl, raPhase, opAmpl and opPhase should change to those values corresponding to the current harmonic. Canvas canvas01 should change to reflect the current harmonic.
|
| User clicks on the Play Sound button. |
- A sound should be played corresponding to the waveform of the sum of sines.
|
| User clicks on the Reset Values button. |
- The amplitude and phase values should reset to the ones which were present at the time of application launch.
|
4. Coding Aspects
As with most HTML5 applications, the software has three parts - the HTML part, the CSS part and JavaScript part. The HTML and CSS parts are quite straightforward in this application; examining these files is a simple exercise. We present more explanations on the JavaScript part here. A small portion of the code uses JQuery as well.
4a. Important Variables
The amplitude and phase values for the ten harmonics are stored in a couple of arrays as follows:
var amplitudeArray = [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1];
var phaseArray = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0];
There is an internal variable called currentHarmonic which is used to store the value of the current harmonic whose parameters the user is varying. The twenty values in the above two arrays are combined to create another array called sineSumValues, which is used to generate the plot showing the sum of sines. For a particular value of the time variable tVal, the computation of the sum of sines is as in the following code extract:
var sineSum = 0.0;
for (var j = 0; j < numberOfHarmonics; ++j){
var val1 = 2 * Math.PI * (j + 1) * tVal + phaseArray[j];
var val2 = amplitudeArray[j] * Math.sin(val1);
sineSum += val2;
}
4b. Drawing on the Canvases displaying 2D Graphs
There are two canvases displaying 2D graphs in this application; these are canvas01 and canvas02. In these canvases, the x-dimension of the graph shows time. Drawing on these two canvases is done as follows:
- Drawing the outer box of the graph, along with the grid. This is done in a function called
drawGraphBox(). This function also draws some of the text content in these two canvases. - Then comes the part of drawing the actual curves. For this, the time dimension, which is 2 seconds in duration, is divided into 400 time instants. For each of these time instants, the ordinate value is computed, and the graph is drawn in a series of
lineTo() canvas function calls, preceded by a single moveTo() call. Care is taken to ensure that the graph drawn is upright, given that the canvas coordinate system has its y-axis pointing downward. - To give the appearance of an animation, the canvas is cleared before each drawing call, using
context.clearRect(). - Some more labels specific to the canvas being drawn are added to the canvas.
For example, the drawing of the lines is done in this code extract:
xPoint0 = xMarginLeft;
yPoint0 = (sineVals[0] - yMin) * yFactor + yLim1;
context01.moveTo(xPoint0, yPoint0);
for( var i = 1; i < sineSumValues.length; ++i) {
xPoint1 = xMarginLeft + i * xStep;
yPoint1 = (sineVals[i] - yMin) * yFactor + yLim1;
context01.lineTo(xPoint1, yPoint1);
}
4c. Drawing on the Canvas displaying 3D Graphs
This pertains to drawing in canvas canvas03. Initially, I felt like using WebGL for drawing the 3D graph; and started embarking on a journey to learn WebGL. However, upon looking more closely at the graph in the SineSum2 Matlab application provided on the Stanford Engineering Everywhere - Fourier Transform site, I felt that simple 2D graphic calls can be cleverly used to create a 3D effect.
- The outer bounding box is just a wireframe, and is drawn as a set of eight lines, using the canvas
moveTo() and lineTo() function calls. This is accompanied by drawing of a grid to enhance the 3D effect. - In the Spectral Plot, each harmonic is characterized by a point denoting its amplitude and phase. Using my knowledge of elementary vector algebra, I defined three vectors, rather three directions - one each for the Harmonic, Phase and Amplitude. Once these directions were defined, it became a straightforward exercise to draw the lines for each spectral point.
- To give a feeling that the spectral line is sitting inside the box, some of the lines of the outer bounding box are drawn before drawing the spectral line, and others are drawn subsequently; so that a z-order is defined, giving the feeling of 3D.
- As before, to give a feeling of animation, the canvas area is cleared using
context.clearRect() before drawing.
4d. Playing the Sound
We use the Web Audio API for generating the sound. This involves creating of an audio context, and then creating the periodic wave corresponding to the amplitude and phase array. Thanks to CP member, M. R. van Mourik, for suggesting this, and also including the relevant code in the Comments to this article.
Earlier, I had used the Riffwave project available on GitHub. This has since been superceded by the Web Audio API in this project.
You may notice that Matlab generates a different sound from what this application generates. The way by which Matlab produces sound is not known to me. You will find that using different amplitudes and phases generates different kinds of sound, and this is expected behaviour.
4e. Other Aspects of Code
- I've not used any frameworks for this application (I'm still a learner), and you may find the code to be plain vanilla. Other than JQuery, which I've used for a small part of the application - to highlight the table row when it is clicked. For this, I've bundled the minified version of JQuery 3.0.0 along with the code.
- I've used IIFE (Immediately Invoked Function Expression), so that you'll find my entire JavaScript code being used as
(function() { /* My code here */ } ()). - To launch the application, just open the file sineSum.html in the browser.
5. Points of Interest
Though I have been programming on and off for nearly three decades now, I am relatively new to HTML5. As a result of this, it is quite possible that there are places where the code is sub-optimal. I request you to kindly point out any such deficiencies in the code, so that I can enrich myself, and improve the code for subsequent versions.
One thing is sure - I thoroughly enjoyed the ecstacies and agonies of developing this application. Learning to program in JavaScript was fun. I hope that you will also enjoy playing with this application. If you feel happy on seeing the graphs dance as you move the sliders, please tell me. If you feel that things need to improve, please don't hesitate to tell me. If any functionality you feel is missing, please write back.
I used Visual Studio Code for developing this application. Really enjoyed using it - an excellent tool from Microsoft.
6. Browser Compatibility
I have tested this on Chrome (Version 51.0.2704.103 m), and Firefox (Version 47.0) on my Windows 7 machine. And on Safari 8.0.8 on my Macbook Pro. Works fine on all these three.
7. Validation
I have tested by giving near-identical values of amplitude and phase to the two programs - the Matlab program and this JavaScript application. The graphs produced by both the programs are alike.
There is one more point for validation. If two or more harmonics have zero phase, and are superposed, the curve has to pass through the points (0, 0), (1, 0), (2, 0) where 0 is the resulting sum at time instants of 0 s, 1 s and 2 s. This is also verified in this JavaScript application. If you find something amiss, please write back to me.
I have taken care to ensure that the user's actions are very limited. This is one way of mistake-proofing the software.
8. Closure
In this article, a simple application to visualize the sum of sines, was presented. This is my first HTML5 application, and enabled me to really learn the three parts - HTML, CSS, JavaScript, with a touch of JQuery. This application is intended as an aid for students to learn the aspects of sum of sines. If that intention is fulfilled for at least one student somewhere, I feel honoured.
The code also available at https://github.com/amarnaths0005/SineSum2.
History
- 30th June, 2016: Version 1.0
- 5th July, 2016: Version 1.1 - Modified the way by which sound was generated
- 8th July, 2016: Version 1.2 - Fixed a bug with respect to playing the sound, reported by ccdsystems
- 24th January, 2023: Added a link to Github pages
Acknowledgements
I would like to thank the following people:
- Professor Brad Osgood, for introducing me to the SineSum Program via Stanford Engineering Everywhere.
- Professor Michel Buffa, for offering the HTML course over the edX platform. This really accelerated my learning of HTML5.
- CodeProject member M. R. van Mourik for suggesting the Web Audio API method of generating sound, and also providing the relevant code extract.
- CodeProject member ccdsystems for pointing out a bug with respect to playing the sound
