TheF#WORD - Crossword Generator

• Download demo application - 926.2 Kb
• Download source code - 460.7 Kb

Introduction

This article discuses algorithm for constructing crossword puzzles. Several techniques and heuristics are described that can reduce search time. The algorithm is implemented in F#.

Background

Crossword construction is a constraint satisfaction problem which belong to NP complexity class. To reduce search space following techniques are employed by the algorithm:

• most constrained variable heuristics - for choosing next pattern to be filled
• least constrained value heuristics - for choosing a word with which selected pattern will be filled
• forward checking - for keeping the list of available words consistent with the current state of crossword
• backjumping - for going back to pattern that is causing inconsistency
• tree pruning - for removing words that are known to lead to the dead ends

All of these subjects are discussed in following sections.

Example

For illustration purposes, simple dictionary is constructed to demonstrate certain behaviors of the algorithm.

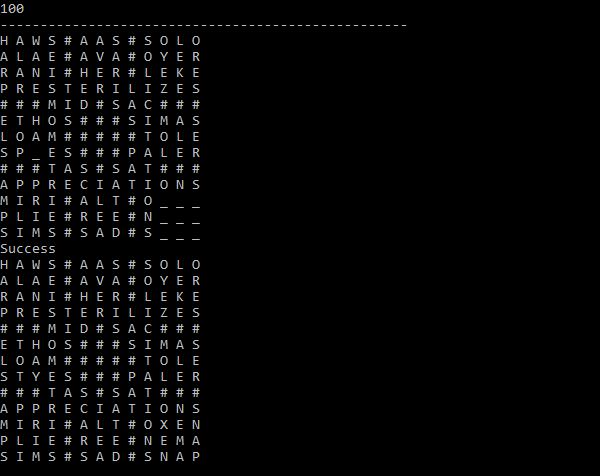
The following image shows a single run of algorithm with the simple dictionary. Also random behaviors are disabled to get reproducible example. This example will be used to show different aspects of the algorithm.

run of the algorithm with the simple dictionary

Crossword Representation

Crossword is represented as two-dimensional array of fields. Each field is described by several properties:

• letter - letter currently occupying the field (special cases: '_' - empty field and '#' block field)
• fill count - stores the number of field's patterns that are currently filled
• conflict marking - indicates that it was not possible to fill one of it's patterns on the latest try due to inconsistency.
• pattern references - index of horizontal and vertical patterns to which the field belongs

Fields are grouped into patterns on which the algorithm operates. Patterns has two important states:

• options - pool of words that are valid for current state of crossword and can be used to fill the pattern.
• stamp - step number of the algorithm in which the pattern was filled.

Horizontal and vertical patterns are kept in separate lists, for faster lookup when searching for connected patterns. Pattern reference is actually an index in these lists. Patterns also have globally unique IDs, so the algorithm can avoid using/processing the same pattern more then once in certain steps.

Pattern Selection

The first thing in each step of the algorithm is to decide which pattern should be filled next. The algorithm selects pattern which has the least number of possible words that can fill it. This is done so the algorithm can hit imminent dead ends sooner rather then later and prune bad search paths early. The heuristic is called most constrained variable.

As it was already said, the algorithm maintains list of valid words for each pattern. This list is called options of the pattern. So to select most constrained pattern it is enough to find pattern with least number of options. Side effect of this approach is that successively filled patterns do not have to be connected, which unfortunately makes backtracking more complicated, but it is worth the hassle.

Word Selection

After the pattern has been selected, then next decision is to choose which word will be used to fill the pattern. This time opposite approach is used. Word which excludes the fewest options from connected pattern is chosen, which leaves greater flexibility in further search. Least constrained value is the name of this heuristic.

Weight of the word is calculated as:

where \(\left | P_{i} \right |\) is number of remaining options for \(i^{th}\) unfilled connected pattern under assumption that word \(w\) is selected. Product instead of summation is used to rule out words which would cause one of the unfilled patterns to become inconsistent (\(\left | P_{i} \right | = 0\)).

Weighting all options of the selected pattern would be too expensive, especially in the early phase of search, so only limited number of words is considered. The algorithm takes only several words from the pool and selects the one with the greatest weight. Once the word is selected it is removed pattern's options.

Forward Checking

Once the word is selected, constraints imposed by the selection are propagated to connected unfilled patterns, so only valid words remain as options for those patterns. This is called forward checking.

This step is necessary, not only for inconsistency checks, but also to get the most constrained variable needed already described. So these two things go hand in hand. It is possible to implement more sophisticated consistency checks such as arc consistency (AC-3 algorithm), but these might be expensive operations.

New set of options for unfilled patterns is already produced by the word selection, needed in order to calculate words' weights, so it will be reused by this phase. The only thing left to do is to save new pattern options.

Backjumping

Once the algorithm finds a pattern that it cannot fill, it has to go back to one of the patterns that was previously filled and fill it with another word in hope the issue will resolved. This is the most complex part of the algorithm.

Naive backtracking approach would be to pick another word for the most recently filled pattern, but it's far from the optimal way. The reason for inefficiency of simple backtracking is order in which the patterns are filled. Since the algorithm fills the most constrained pattern first, patterns filled in two successive steps might not be connected at all. If that is the case, then changing the word of the first pattern will not resolve inconsistency in the second, it will only waste CPU cycles.

Better approach is to go back only to the patterns that are connected to the one that is inconsistent. This technique is called backjumping.

To solve this issue, the algorithm stamps each filled pattern with a step number in which it was filled. This addition makes it is possible to recover the order in which patterns were filled. Now it can be determined which pattern should be changed as well as the list of all patterns affected by that change.

Steps performed by backjump are following:

1. Mark all fields of inconsistent pattern as conflicted

   The algorithm simply set conflict marking for each field of the inconsistent pattern.

2. Identify target pattern to which the algorithm needs to backujump

   Target is the most recently filled pattern that has been filled earlier than and is connected to the one which is inconsistent. To determine which pattern satisfy this condition, the algorithms uses previously described stamps. If no such pattern is found, the most recently filled pattern globally is used as target.

   backjump to pattern that is not connected

   Steps #8 and #9 demonstrate this situation. If that fails as well, it means the search is back at the beginning with no more options available. This indicates end of search and failure to construct crossword.

3. Undo all patterns that depends on the target of backjump

   Once the target is located, all patterns depending on it must be undone. To generate list of these patterns, the algorithm starts from the target and adds all connected patterns that are filled after the target. The process is repeated recursively for each new pattern added to the list. Once the list is completed, fields of patterns in the list are updated with new fill count and cleared if necessary.

4. Restore options for all affected patterns

   List of possible words for each undone pattern must be regenerated, based on the values of underlying fields which remained filled. Undo process, that was previously described, also affects unfilled patterns connected to those that are undone. So the final list of affected patterns is union of cleared patterns and unfilled patterns connected to them. For each pattern in the list, the algorithm forms the list of words by matching the words from dictionary against the state of pattern's fields.

5. Prune options of target pattern

   Pruning process is described in the following section.

Tree Pruning

Once the algorithm backtracks it is possible to determine which parts of target pattern caused the problem, so options that are going to repeat the same mistake can be removed from list of valid options.

To prune options, the algorithm will construct filter based on conflicting markings of pattern's fields. As it already said, each time an inconsistent pattern is found all of it's field are marked as conflicted. These markings are preserved and accumulated across backjumps and they are cleared only when the pattern is filled successfully.

mark fields of inconsistent pattern as conflicted	clear conflict mark after filling the pattern

When backjump reaches its target all it needs to do is to remove words that have matches the pattern of marked fields.

pruning in action

Effects of pruning can be seen between step #9 and #10. After AAAAA word had failed to produce solution, the algorithm selected DDDBB even thought there was BBBAAA before it in dictionary. The approach is rather simple and it is possible do develop more sophisticated algorithm that would prune even more options by constructing less restrictive filters, but it was not not implemented.

non-optimal prune filter

This potential sequence of tries would create ___AA filter for pruning, but since those two inconsistent patterns are not dependent, much better option would be to create two filters: ___A_ and ____A as this pair would remove greater number of options.

Code

Field of crossword is represented by CwField record:

type CwField = 
    { Letter : char
      HorRef : int
      VerRef : int
      Count : int
      Conflicted : bool }

Patterns are represented by CwPattern class:

type CwPattern(grid : CwField [,], dictionary : string array,
    direction : CwDirection, no : int, xs : int, ys : int, length : int) = 
    
    // prune current options according filter produced
    // using conflicted markings on underlying fields
    member m.PruneOptions()
    
    // restore all options according to state of underlying fields
    member m.RestoreOptions()
    
    // sets new options for the pattern
    // options generated by the algorithm during word selection phase
    member m.UpdateOptions(opts : string array)
    
    // updates underlying fields with letters and increment their fill count
    // removes the word from remaining options
    member m.Fill(word : string, step : int)
    
    // clears letters of underlying fields and decreases their fill count,
    // but it keeps remaining options
    member m.Undo()
    
    // marks all underlying fields of pattern as conflicted
    member m.MarkConflicted()
    
    // array of letters in stored in underlying fields
    member m.Letters
    
    // tests whether any underlying field is marked as conflicted
    member m.Conflicted
    
    // string of letters in stored in underlying fields
    member m.Word
    
    // unique ID of the pattern in the crossword
    member m.No
    
    // X position of the first field
    member m.X
    
    // X position of the first field
    member m.Y
    
    // number of letters in the pattern
    member m.Length 
    
    // direction of the pattern: horizontal or vertical
    member m.Direction
    
    // array of all remaining options
    member m.Options 
    
    // number of options remaining 
    member m.Count 
    
    // step number if the algorithm in which the pattern was filled
    member m.Stamp

Crossword is represented by Crossword class:

type Crossword(filePath : string, dictionary : CwDictionary) = 
    // minimal pattern length
    // shorter patterns are not considered during the construction
    let minPatternLength
    
    // maximal number of words that are taken into account
    // when selecting word for a pattern
    let maxWordPoolLength
    
    // two-dimensional array of fields
    let grid

    // horizontal and vertical patterns
    let hPatterns 
    let vPatterns 

    // returns list of crossword's patterns that are orthogonal
    // to specified pattern 
    let orthogonal (pattern : CwPattern)
    
    // selects pattern from queue of unfilled patterns
    let selectPattern queue
    
    // selects word for specified pattern
    let selectWord (pattern : CwPattern)
    
    // finds the target of backjump, clears the patterns
    // and return them to queue
    let backjump (start : CwPattern)
    
    // main loop of the algorithm
    member x.Solve(refreshRate : int)
    
    // checks whether all patterns are correctly filled
    member x.Check()
    
    // prints crossword on console
    member x.Print()

Dictionary and Puzzle Files

Dictionary is stored in words.txt file, while the puzzle structure is defined by puzzle.txt. '.' represents free field and '#' is block field.

References

• Constructing Crossword Grids: Use of Heuristics vs Constraints
• Search Lessons Learned from Crossword Puzzles

History

2017-03-14 - Initial version posted