Introduction
Heard of Bitwise operators in T-SQL? The following two SQL statements will produce the same results. Notice the use of the Ampersand '&' in the join in the first statement. This Bitwise operator eliminates the need for an entire table join.
Select * From bp.Party bp Inner Join bp.PartyItem pi _
On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag Where bp.ID = 99
Select * From bp.Party bp Inner Join bp.PartyToPartyItem bppi _
On bp.ID = bppi.ID Inner Join bp.PartyItem pi _
On bppi.BitFlag = pi.BitFlag Where bp.ID = 99
Read on to learn when and how a Bitwise table join might make sense in your data model!
Background
I have heard some developers express a desire to leverage bitwise table joins to simplify the management of data for maintaining and leveraging many-to-many relationships. Responses I have heard run the gammut from something like "NOOOO, DON'T DO IT - you won't be enforcing referential integrity!!" to "Sometimes it makes sense to violate the rules if you get enough benefit."
So I started wondering, "Are these really the only two options at the opposite ends of the spectrum? Why can't we have our cake and eat it too? Can't we obtain the benefit of using bitwise operators for SQL many-to-many relationships AND maintain referential integrity? Do these really have to be mutually exclusive?" As I pondered over this, I was convinced that "Even if there are some trade-offs, there must be some decent middle ground somewhere!"
So I decided to check into it. What I found is that it is not only possible, but it is actually not that difficult. And it can be expressed in a relational table design pattern that is very reasonable for certain use cases. There are in fact many potential benefits, more actually than I supposed. These can include simplification of queries, reduced disk I/O, reduced record count, increased performance of specific queries, better support for application development, finer-grained many-to-many relationship rule enforcement and increased flexibility.
Here is what I plan to cover in this article:
- A Quick Bitwise Operations Tutorial
- A Comparison of Methods With "Birthday Parties, Inc.":
- Method One: Queries with Just Two Tables Using Bitwise Operators
- Method Two: Obtaining the Same Output Using Traditional Bridging Table
- Method Three: Exploring New Method Replacing Large Bridging Table With Two Smaller Tables
- Comparing Queries Returning Larger Data Sets
- Comparing Methods for Performing Updates
- Impact of Adding New Party Items
- Consideration of a Real-World Use Case
- Benefits and Caveats
- Conclusion
Note: The code provided in this article is nuanced for SQL Server, but should be easily retoolable for any modern mainstream RDBMS.
Note: I have minimized the use of common table expressions (i.e., using "with") to keep the queries more straightfoward. Please feel free to make your own improvements.
A "Quick" Bitwise Operations Tutorial
Note: Quick does not necessarily mean "extremely short"! If you are already familiar with bitwise operations, feel free to skip to "Birthday Parties, Inc."
Note: This tutorial will only address bitwise operations for positive numerical values.
Bit (the "Bit" is "It"!)
"Bit," short for "binary digit," is the fundamental building block in computing. It is a single place binary number the value of which can be set to one of only two values, either 0 or 1. In programming, these values are often stored in boolean variables where the values may be referred to as TRUE or FALSE, YES or NO, ON or OFF or simply 1 or 0.
Binary Numbers and Bit Flags
When a bit is used to manage two possible states of a defined item, it is often referred to as a "bit flag" or sometimes just a "flag." The value of the bit flag (0 or 1) indicates whether the item's bit is set ON (1) or OFF (0).
Binary numbers contain a "string" of binary digits where each digit is a bit that may be set to either 0 or 1. Therefore, each bit in the binary number, or string, may be used as a bit flag for a uniquely defined item.
Binary Numbers, Bit Flags and Integers
There is a special relationship between binary numbers and integers. Except for 0, each digit in a binary number corresponds to an integer with a successive power of 2:
Binary Decimal Bit Position
00000000 = 0 No bits set
00000001 = 1 First bit set
00000010 = 2 Second bit set
00000100 = 4 Third bit set
00001000 = 8 Fourth bit set
00010000 = 16 Fifth bit set
00100000 = 32 Sixth bit set
01000000 = 64 Seventh bit set
etc.
This is the base set of integers to keep in mind for our bitwise operations. When defined items are assigned to these, they may be referred to by many terms including "set of bit flags," "bit flag list," "flag list" or simply "flags." In this article, I may use the term "bit flag" or just "bit" when referring to individual integer elements from a flag list.
Example:
Party Item Bit Flags
0 = Nothing
1 = Cake
2 = Ice Cream
4 = Happy Birthday Banner
8 = Party Streamers
16 = Balloons
32 = Party Hats
64 = Pinatta
In application code, these may sometimes be assigned through a set of constants. The syntax can look quite different in various languages, but a similar pattern should be recognizable.
Example from VB:
Const NONE As Int = 0
Const CAKE As Int = 1
Const ICE_CREAM As Int = 2
Const BANNER As Int = 4
Const STREAMERS As Int = 8
Const BALLOONS As Int = 16
Const HATS As Int = 32
Const PINATTA As Int = 64
Bit Flag Encoded Integers
So what about the integers 3 and 5? Or 6, 7 and 9? Using our base set of bit flags as the context, the "in between" integers represent combinations of the base flags. The flag combination present in any particular integer tells us which bits are set ON and OFF. When an integer contains a particular flag, its representative bit is said to be set ON, and when absent, it is said to be set OFF.
For instance:
- The integer 3 indicates that both the first (1) and second (2) bits are set to ON: 3 = 2 + 1 (in case you want both Cake AND Ice Cream)
- The integer 5 indicates that the first (1) and third (4) bits are set to ON: 5 = 4 + 1 (Happy Birthday Banner + Cake)
In the same way, every integer (up to the sum of all of our flags) can be decomposed into a set of one or more of our bit flags. The full set of integers that can be derived from our base bit flags we'll call "bit flag encoded integers."
Using some of our party items, the following shows how, with a full list of integers, we can encode any combination of our original list of bit flags:
1 = 1 Just Cake
2 = 2 Just Ice Cream
3 = 2 + 1 Ice Cream + Cake
4 = 4 Just Happy Birthday Banner
5 = 4 + 1 Happy Birthday Banner + Cake
6 = 4 + 2 Happy Birthday Banner + Ice Cream
7 = 4 + 2 + 1 Happy Birthday Banner + Ice Cream + Cake
8 = 8 Just Party Streamers
9 = 8 + 1 Party Streamers + Cake
10 = 8 + 2 Party Streamers + Ice Cream
11 = 8 + 2 + 1 Party Streamers + Ice Cream + Cake
12 = 8 + 4 Party Streamers + Happy Birthday Banner
13 = 8 + 4 + 1 Party Streamers + Happy Birthday Banner + Cake
14 = 8 + 4 + 2 Party Streamers + Happy Birthday Banner + Ice Cream
15 = 8 + 4 + 2 + 1 Party Streamers + Happy Birthday Banner + Ice Cream + Cake
16 = 16 Just Balloons
17 = 16 + 1 Balloons + Cake
etc.
Bitwise Operators
Bitwise operators are fundamental to core computing processes, but are different from what is typically used in everyday math. They are not necessarily difficult to use, just different. The beauty of bitwise operators, is that they allow us to do some pretty cool things with our bit flag encoded integers.
- The AND Operator ( & in SQL Server)
- This operator takes an intersection of the bits that are set ON between two integers and returns a third that has just those bits set
ON. 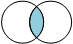
- Example:
- 2 + 1 = 3; 4 + 2 = 6; 3 & 6 = 2; 2 is the only bit that 3 and 6 both have in common
- 3 = Ice Cream + Cake
- 6 = Happy Birthday Banner + Cake
- 3 & 6 = Cake (2)
- Example:
- 8 + 4 + 1 = 13; 16 + 8 + 4 + 2 = 30; 13 & 30 = 12; 12 = the combined bits that 13 and 30 both have in common: 8 + 4 = 12
- 13 = Party Streamers + Happy Birthday Banner + Cake
- 30 = Balloons + Party Streamers + Happy Birthday Banner + Ice Cream
- 13 & 30 = Party Streamers + Happy Birthday Banner (12)
- The OR Operator ( | in SQL Server)
- The
OR operator takes a union of all the bits that are set ON in two integers and returns a third that has all those bits set ON. 
- Example:
- 2 + 1 = 3; 4 + 2 = 6; 3 | 6 = 7; the bits that are set
ON across both 3 and 6 are 1, 2 and 4; 4 + 2 + 1 = 7 - 3 = Ice Cream + Cake
- 6 = Happy Birthday Banner + Cake
- 3 | 6 = Happy Birthday Banner + Cake + Ice Cream (7)
- The NOT Operator ( ~ in SQL Server)
- The
NOT operator reverses the bit values in an integer so those that were ON are now OFF and those that were OFF are now ON. This is not particularly helpful alone for our purposes, but when combined with the AND operator becomes very handy.
- Combining AND plus NOT ( &~ in SQL Server)
- This operator combination subtracts the bits set ON in the second integer from the bits set ON in the first and then returns a third with just the remaining bits set
ON. 
- Example:
- 8 + 4 + 2 = 14; 14 &~ 8 = 6
- 14 = Party Streamers (we want to remove) + Happy Birthday Banner + Ice Cream
- Removing Party Streamers (8) from 14 leaves us with Happy Birthday Banner + Ice Cream (6)
- The XOR Operator ( ^ in SQL Server)
- The
XOR operator takes the union of, minus the intersection of, the bits set ON from two integers and returns a third with the resulting bits set ON. 
- This operation is more complicated and is often used for encryption purposes. We will not be dealing with the
XOR operator here.
Bitwise Usage Patterns for SQL
Here are the typical usage patterns for SQL I will cover in this article:
- & (AND): The & operator is particularly helpful in determining whether a bit flag encoded integer contains one or more bit flags.
- Example:
- "Select 7 & 4" returns 4 because 7 = 1 + 2 + 4.
- | (OR): The | operator is useful in adding bit flags to a new or existing bit flag encoded integer.
- Examples:
- "Select 1 | 2 | 4 | 8" returns 15 because 15 = 1 + 2 + 4 + 8
- "Select 15 | 16" returns 31 because 31 = 15 (1 + 2 + 4 + 8) + 16
- Note that the ADD operator ( + ) can be used in place of the
OR ( | ) operator for generating bit flag encoded integers but only when using values from the base set of flags, and only once per flag. This is helpful when creating a combination of bit flags from scratch. The difference is that duplicate bit flags can be ORd multiple times without negative effect while the same is not true for the ADD operator. This is because once a bit is set ON, setting it ON again using OR has no effect, but using the ADD operator would incorrectly add the integer a second time, and the second time it would not be treated as a flag. - Examples:
- "
Select (1 | 2)" equals "Select (1 + 2)" BUT "Select (1 | 1)" does NOT equal "Select (1 + 1)" - "
Select (1 | 2 | 1 | 2)" equals "Select (1 | 2)" BUT it does NOT equal "Select (1 + 2 + 1 + 2)"
- &~ (AND NOT): The &~ operator combination is particularly helpful in removing one or more flags from an existing bit flag encoded integer if they exist.
- Examples:
- "Select 15 &~ 8" removes bit flag 8 from the bit flag encoded integer 15 returning 7.
- "Select 31 &~ 6" removes bit flags 4 and 2 (6 = 2 + 4) from the bit flag encoded integer 31 returning 25.
- Note that the SUBTRACT operator ( - ) COULD potentially be used to remove bit flags, but I highly recommend NOT doing that. It would have to be absolutely ensured that a bit flag is set ON in an integer before using SUBTRACT. The following is an example of how you can obtain unintended consequences.
- Task: Remove bit flag 32 from a bit flag encoded integer IF it is set ON.
- Example using AND NOT (&~):
- "Select 31 &~ 32" correctly returns 31 because bit flag 32 was not included in the bit flag encoded integer 31 and setting bits OFF that are already OFF has no effect.
- Example using SUBTRACT (-):
- "Select 31 - 32" returns (-1) because we did not first ensure that the bit flag encoded integer 31 even included flag 32 to begin with - we should not have executed this.
- It is easy to see the problem with actual integer values, but image how easy it might be to introduce an error using (-) instead of (&~) on bit flag encoded integer values in variables or fields.
Using Bitwise Operators Compared to Traditional Method
Birthday Parties, Inc.
Now let's set up a database example to show how these operators can be used for table operations in comparison with traditional methods.
Continuing with our birthday party items example, suppose you own a company that caters birthday parties. You are doing quite well, because you have a database that contains one million parties!
You offer thirteen different party items and are considering adding a couple more. For any given party, there can be any combination of zero or more party items included in the package. You need to query and update which parties have which party items.
To start, in your SQL Server environment, execute "Setup Script 1a" and "Setup Script 1b" to set up the initial environment.
NOTE: Using the scripts provided, the table "bp.Party" is loaded with one million records. If you do not wish to load this many records, modify "Setup Script 1b.sql" to reduce the number of names loaded into the temporary tables that are used to generate records for "bp.Party".
Create Schema bp
GO
Create Table bp.PartyItem(
BitFlag Int NOT NULL
, ItemName Varchar(40) NOT NULL
)
GO
ALTER TABLE bp.PartyItem ADD CONSTRAINT PK_PartyItem_BitFlag PRIMARY KEY CLUSTERED
(
BitFlag ASC
)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE = OFF, _
SORT_IN_TEMPDB = OFF, IGNORE_DUP_KEY = OFF, ONLINE = OFF, _
ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON) ON [PRIMARY]
GO
ALTER TABLE bp.PartyItem
ADD CONSTRAINT chkFlagValue CHECK (BitFlag & (BitFlag - 1) = 0);
GO
Insert bp.PartyItem(BitFlag, ItemName) Values(0, 'Nothing')
Insert bp.PartyItem(BitFlag, ItemName) Values(1, 'Cake')
Insert bp.PartyItem(BitFlag, ItemName) Values(2, 'Ice Cream')
Insert bp.PartyItem(BitFlag, ItemName) Values(4, 'Happy Birthday Banner')
Insert bp.PartyItem(BitFlag, ItemName) Values(8, 'Party Streamers')
Insert bp.PartyItem(BitFlag, ItemName) Values(16, 'Balloons')
Insert bp.PartyItem(BitFlag, ItemName) Values(32, 'Party Hats')
Insert bp.PartyItem(BitFlag, ItemName) Values(64, 'Pinatta')
Insert bp.PartyItem(BitFlag, ItemName) Values(128, 'Party Favors')
Insert bp.PartyItem(BitFlag, ItemName) Values(256, 'Confetti Poppers')
Insert bp.PartyItem(BitFlag, ItemName) Values(512, 'Party Blowers')
Insert bp.PartyItem(BitFlag, ItemName) Values(1024, 'Games')
Insert bp.PartyItem(BitFlag, ItemName) Values(2048, 'Prizes')
After executing the script above, open and execute "Setup Script 1b.sql" (it is too long to post here).
Now that we have our initial environment setup, let's look at our first method.
Method One: Queries with Just Two Tables Using Bitwise Operators
Note: The query outputs for Method One, Method Two and Method Three should be identical.
Associated ERD:

Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItem pi On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag
Where bp.ID = 401409
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItem pi On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag
Where bp.ID = 503808
And pi.BitFlag <> 0
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItem pi On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag
Where bp.ID = 600120
And pi.BitFlag <> 0
This is the method I have heard desired and / or used by some to simplify many-to-many relationship data management.
Benefits of Method One:
- Allows storage of boolean information for numerous flags in a small space common to application coding practice
- Supports use of the
AND, OR, NOT and XOR bitwise operators ( "&," "|," "~" and "^" in SQL Server) to simplify queries - Provides for in-place updates for managing changes minimizing database disk I/O
Drawbacks:
- Does not enforce referential integrity
- Does not generally provide the benefits of indexing
Let's move on to Method Two...
Method Two: Obtaining the Same Output Using Traditional Bridging Table
Associated ERD:

Additional setup for Method Two:
Create Table bp.PartyToPartyItem(
ID Int
, BitFlag Int
)
GO
ALTER TABLE bp.PartyToPartyItem WITH CHECK ADD CONSTRAINT _
[FK_PartyToPartyItem_Party] FOREIGN KEY([ID])
REFERENCES bp.Party ([ID])
GO
ALTER TABLE bp.PartyToPartyItem CHECK CONSTRAINT [FK_PartyToPartyItem_Party]
GO
ALTER TABLE bp.PartyToPartyItem WITH CHECK ADD CONSTRAINT _
[FK_PartyToPartyItem_PartyItem] FOREIGN KEY([BitFlag])
REFERENCES bp.PartyItem ([BitFlag])
GO
ALTER TABLE bp.PartyToPartyItem CHECK CONSTRAINT [FK_PartyToPartyItem_PartyItem]
GO
Insert bp.PartyToPartyItem(ID, BitFlag)
Select bp.ID
, pi.BitFlag
From bp.Party bp
Inner Join bp.PartyItem pi On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag
Where ((bp.PartyItemFlags = 0 And pi.BitFlag = 0)
Or (bp.PartyItemFlags > 0 And pi.BitFlag > 0))
And Not Exists (Select ID From bp.PartyToPartyItem Where ID = bp.ID _
And BitFlag = pi.BitFlag)
Okay, let's try out Method Two!
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyToPartyItem bppi On bp.ID = bppi.ID
Inner Join bp.PartyItem pi On bppi.BitFlag = pi.BitFlag
Where bp.ID = 401409
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyToPartyItem bppi On bp.ID = bppi.ID
Inner Join bp.PartyItem pi On bppi.BitFlag = pi.BitFlag
Where bp.ID = 503808
Order By pi.BitFlag
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyToPartyItem bppi On bp.ID = bppi.ID
Inner Join bp.PartyItem pi On bppi.BitFlag = pi.BitFlag
Where bp.ID = 600120
Order By pi.BitFlag
Benefits of Method Two:
- Enforces referential integrity
- Easily supports indexing
Drawbacks:
- Requires maintenance of potentially large numbers of records (5,999,349 in this case)
- Queries can quickly become complex (as we'll see shortly)
- Entries are continuously inserted to and deleted from the bridging table increasing disk I/O
Now let's take a look at Method Three...
Method Three: Exploring New Method Replacing Large Bridging Table With Two Smaller Tables
Associated ERD:

Setup for Method Three:
Create Table bp.PartyItems(
BitFlags Int NOT NULL
)
GO
ALTER TABLE bp.PartyItems ADD CONSTRAINT PK_PartyItems_BitFlags PRIMARY KEY CLUSTERED
(
BitFlags ASC
)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE = OFF, _
SORT_IN_TEMPDB = OFF, IGNORE_DUP_KEY = OFF, ONLINE = OFF, _
ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON) ON [PRIMARY]
GO
With bfc As (
Select 0 As RowNumber
UNION
Select Row_Number() Over (Order By pi1.BitFlag) As RowNumber
From bp.PartyItem pi1
Cross Join bp.PartyItem pi2
Cross Join bp.PartyItem pi3
Cross Join bp.PartyItem pi4
)
Insert bp.PartyItems(BitFlags)
Select RowNumber
From bfc
Where RowNumber <= (Select Sum(BitFlag) From bp.PartyItem)
And Not Exists (Select * From bp.PartyItems Where BitFlags = bfc.RowNumber)
ALTER TABLE bp.Party WITH CHECK ADD CONSTRAINT [FK_Party_PartyItems] _
FOREIGN KEY([PartyItemFlags])
REFERENCES bp.PartyItems ([BitFlags])
GO
ALTER TABLE bp.Party CHECK CONSTRAINT [FK_Party_PartyItems]
GO
Create Table bp.PartyItemToPartyItems(
BitFlag Int
, BitFlags Int
)
GO
ALTER TABLE bp.PartyItemToPartyItems WITH CHECK ADD _
CONSTRAINT [FK_PartyToPartyItems_PartyItem] FOREIGN KEY([BitFlag])
REFERENCES bp.PartyItem ([BitFlag])
GO
ALTER TABLE bp.PartyItemToPartyItems CHECK CONSTRAINT [FK_PartyToPartyItems_PartyItem]
GO
ALTER TABLE bp.PartyItemToPartyItems _
WITH CHECK ADD CONSTRAINT [FK_PartyToPartyItem_PartyItems] FOREIGN KEY([BitFlags])
REFERENCES bp.PartyItems ([BitFlags])
GO
ALTER TABLE bp.PartyItemToPartyItems CHECK CONSTRAINT [FK_PartyToPartyItem_PartyItems]
GO
Insert bp.PartyItemToPartyItems(BitFlag, BitFlags)
Select pi.BitFlag
, pis.BitFlags
From bp.PartyItem pi
Inner Join bp.PartyItems pis On pi.BitFlag & pis.BitFlags = pi.BitFlag
Where ((pis.BitFlags = 0 And pi.BitFlag = 0)
Or (pis.BitFlags > 0 And pi.BitFlag > 0))
And Not Exists (Select BitFlag From bp.PartyItemToPartyItems _
Where BitFlag = pi.BitFlag And BitFlags = pis.BitFlags)
And, test Method Three using traditional queries:
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, bp.LastName, _
bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItems pis On bp.PartyItemFlags = pis.BitFlags
Inner Join bp.PartyItemToPartyItems pipis On bp.PartyItemFlags = pipis.BitFlags
Inner Join bp.PartyItem pi On pipis.BitFlag = pi.BitFlag
Where bp.ID = 401409
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItems pis On bp.PartyItemFlags = pis.BitFlags
Inner Join bp.PartyItemToPartyItems pipis On bp.PartyItemFlags = pipis.BitFlags
Inner Join bp.PartyItem pi On pipis.BitFlag = pi.BitFlag
Where bp.ID = 503808
Order By pi.BitFlag
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItems pis On bp.PartyItemFlags = pis.BitFlags
Inner Join bp.PartyItemToPartyItems pipis On bp.PartyItemFlags = pipis.BitFlags
Inner Join bp.PartyItem pi On pipis.BitFlag = pi.BitFlag
Where bp.ID = 600120
Order By pi.BitFlag
We added 28,673 new records, but now have referential integrity using our bitflag values. This means we no longer need our original 5,999,349 row bridging table.
That is a pretty good trade-off... we replaced one table of 5,999,349 records with two tables of 28,673 records!
- 5,999,349 - (4,096 + 24,577) = 5,970,676 saved records
And since we have now succeeded in enforcing referential integrity using our actual bitwise flags values, if it is reasonable to do so, there is no reason a developer cannot use the original more simplified queries from Method One!
Benefits of Method Three:
- All the benefits of Method One plus...
- Enforces referential integrity
- Provides the flexibility to build queries using both bitwise operators and / or traditional methods
- Easily supports use of indexes for traditional queries
Drawbacks:
- Adds one additional table to the overall table count
- Only suitable for certain many-to-many relationship scenarios (not really a drawback, just a caution)
Comparing Queries Returning Larger Data Sets
Now let's see what happens when we try to return all the parties with specific party items. This is where we start seeing the complexity tradeoff.
Task 1: Find all the parties that include 'Cake,' 'Ice Cream,' 'Happy Birthday Banner,' 'Party Streamers,' 'Balloons' and 'Party Hats':
Select * From bp.Party Where PartyItemFlags & 63 = 63
And PartyItemFlags >= 63
Select * From bp.Party Where PartyItemFlags & (1|2|4|8|16|32) = (1|2|4|8|16|32)
And PartyItemFlags >= (1|2|4|8|16|32)
Select * From bp.Party Where PartyItemFlags & (1+2+4+8+16+32) = (1+2+4+8+16+32)
And PartyItemFlags >= (1+2+4+8+16+32)
Select *
From bp.Party
Where PartyItemFlags
& (Select Sum(BitFlag) From bp.PartyItem Where ItemName _
In ('Cake', 'Ice Cream', 'Happy Birthday Banner', 'Party Streamers', _
'Balloons', 'Party Hats'))
= (Select Sum(BitFlag) From bp.PartyItem Where ItemName In _
('Cake', 'Ice Cream', 'Happy Birthday Banner', 'Party Streamers', _
'Balloons', 'Party Hats'))
And PartyItemFlags >= (Select Sum(BitFlag) From bp.PartyItem _
Where ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats'))
Select Distinct p.*
From bp.Party p
Where (Select Sum(BitFlag) & p.PartyItemFlags From bp.PartyItem _
Where ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats'))
= (Select Sum(BitFlag) From bp.PartyItem Where ItemName _
In ('Cake', 'Ice Cream', 'Happy Birthday Banner', 'Party Streamers', _
'Balloons', 'Party Hats'))
And PartyItemFlags >= (Select Sum(BitFlag) From bp.PartyItem _
Where ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats'))
Select a.*
From bp.Party a
, bp.PartyItem b
, bp.PartyItem c
, bp.PartyItem d
, bp.PartyItem e
, bp.PartyItem f
, bp.PartyItem g
Where a.PartyItemFlags & b.BitFlag = b.BitFlag And b.ItemName = 'Cake'
And a.PartyItemFlags & c.BitFlag = c.BitFlag And c.ItemName = 'Ice Cream'
And a.PartyItemFlags & d.BitFlag = d.BitFlag And d.ItemName = 'Happy Birthday Banner'
And a.PartyItemFlags & e.BitFlag = e.BitFlag And e.ItemName = 'Party Streamers'
And a.PartyItemFlags & f.BitFlag = f.BitFlag And f.ItemName = 'Balloons'
And a.PartyItemFlags & g.BitFlag = g.BitFlag And g.ItemName = 'Party Hats'
Select p.*
From bp.Party p
Inner Join
( Select ppi.ID
From bp.PartyToPartyItem ppi
Inner Join bp.PartyItem pi On ppi.BitFlag = pi.BitFlag _
And pi.ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats')
Group By ppi.ID
Having Count(ppi.ID) = (Select Count(BitFlag) From bp.PartyItem _
Where ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats'))
) fss On p.ID = fss.ID
Task 2: Find all the parties that ONLY include 'Cake,' 'Ice Cream,' 'Happy Birthday Banner,' 'Party Streamers,' 'Balloons' and 'Party Hats'. Here, we see reduced complexity and improved peformance:
Select * From bp.Party Where PartyItemFlags = 63
Select * From bp.Party Where PartyItemFlags = (Select Sum(BitFlag) _
From bp.PartyItem Where ItemName In ('Cake', 'Ice Cream', _
'Happy Birthday Banner', 'Party Streamers', 'Balloons', 'Party Hats'))
Select p.*
From bp.Party p
Inner Join
( Select ppi.ID
From bp.PartyToPartyItem ppi
Inner Join bp.PartyItem pi On ppi.BitFlag = pi.BitFlag _
And pi.ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats')
Group By ppi.ID
Having Count(ppi.ID) = (Select Count(BitFlag) From bp.PartyItem _
Where ItemName In ('Cake', 'Ice Cream', 'Happy Birthday Banner', _
'Party Streamers', 'Balloons', 'Party Hats'))
) fss On p.ID = fss.ID
Where (Select Count(BitFlag) From bp.PartyToPartyItem Where ID = p.ID) = _
(Select Count(BitFlag) From bp.PartyItem Where ItemName In _
('Cake', 'Ice Cream', 'Happy Birthday Banner', 'Party Streamers', _
'Balloons', 'Party Hats'))
Comparing Methods for Performing Updates
So how do the methods compare when updating data? This is where bitwise operators really shine!
Update bp.Party Set PartyItemFlags = PartyItemFlags | 64
Where ID = 600120
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItem pi On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag
Where bp.ID = 600120
And pi.BitFlag <> 0
Update bp.Party Set PartyItemFlags = PartyItemFlags & ~64
Where ID = 600120
Update bp.Party Set PartyItemFlags = PartyItemFlags | 1024
Where ID = 600120
Update bp.Party Set PartyItemFlags = PartyItemFlags &~ 64 | 1024
Where ID = 600120
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyItem pi On bp.PartyItemFlags & pi.BitFlag = pi.BitFlag
Where bp.ID = 600120
And pi.BitFlag <> 0
Insert bp.PartyToPartyItem(ID, BitFlag)
Select ID = 600120
, BitFlag = 64
Delete bp.PartyToPartyItem Where ID = 600120 And BitFlag = 64
Insert bp.PartyToPartyItem(ID, BitFlag)
Select ID = 600120
, BitFlag = 1024
Select bp.ID, bp.GenderCode, bp.FirstName, bp.MiddleName, _
bp.LastName, bp.PartyItemFlags, pi.BitFlag, pi.ItemName
From bp.Party bp
Inner Join bp.PartyToPartyItem bppi On bp.ID = bppi.ID
Inner Join bp.PartyItem pi On bppi.BitFlag = pi.BitFlag
Where bp.ID = 600120
Order By pi.BitFlag
Impact of Adding New Party Items
What if we want to add new party items? Our new method incurs a one-time cost for inserting a few records rewarded by the continued elimination of the daily need for inserts and deletes from the traditional bridging table.
Insert bp.PartyItem(BitFlag, ItemName) Values(4096, 'Clown')
Insert bp.PartyItem(BitFlag, ItemName) Values(8192, 'Pizza')
With bfc As (
Select 0 As RowNumber
UNION
Select Row_Number() Over (Order By pi1.BitFlag) As RowNumber
From bp.PartyItem pi1
Cross Join bp.PartyItem pi2
Cross Join bp.PartyItem pi3
Cross Join bp.PartyItem pi4
)
Insert bp.PartyItems(BitFlags)
Select RowNumber
From bfc
Where RowNumber <= (Select Sum(BitFlag) From bp.PartyItem)
And Not Exists (Select * From bp.PartyItems Where BitFlags = bfc.RowNumber)
Insert bp.PartyItemToPartyItems(BitFlag, BitFlags)
Select pi.BitFlag
, pis.BitFlags
From bp.PartyItem pi
Inner Join bp.PartyItems pis On pi.BitFlag & pis.BitFlags = pi.BitFlag
Where ((pis.BitFlags = 0 And pi.BitFlag = 0)
Or (pis.BitFlags > 0 And pi.BitFlag > 0))
And Not Exists (Select BitFlag From bp.PartyItemToPartyItems _
Where BitFlag = pi.BitFlag And BitFlags = pis.BitFlags)
Consideration of a Real-World Use Case
So where might this be used in a real-world scenario?
One example where this pattern may be helpful is for storing and retrieving user / role permissions that are used dynamically in an application, especially when permissions for multiple user roles must be aggregated on the fly to determine effective permissions, e.g., returning the greatest and / or least permissions.
Consider the following where 1 = Create, 2 = Read, 4 = Update, 8 = Delete and 16 = Execute:
- User Role 1: Has Read and Execute = 2 + 16 = 18
- User Role 2: Has Create, Read, Update and Delete = 1 + 2 + 4 + 8 = 15
Effective Permissions:
- Additive (
OR): 18 | 15 = 31 (Create, Read, Update, Delete, Execute) - Intersection (
AND): 18 & 15 = 2 (Read)
Summary
Benefits and Caveats
So here is how I see this breaking down.
General Benefits
- Can be used to simplify certain many-to-many relationship queries with the use of bitwise operators
- Allows storage of bit information for numerous flags in a small space in a method also common to application coding practice
- Continues to enforce referential integrity
- Has the potential to greatly reduce record count
- Can increase performance for certain queries
- Provides increased flexibility:
- Supports use of the bitwise operators
- Supports traditional query methodology for query designers not familiar with bitwise operators
- Supports any valid combination thereof
- Minimizes day-to-day disk I/O by providing for in-place updates rather than expensive inserts and deletes
Benefits for Application Development
- Application developers could have the option of relying on the database for their bit flag list instead of hard coded constants.
- Bit flag tables can be used in the database to enforce bit flags and bit encoded values that already exist in the application.
- Data is already in the format needed to perform bitwise operations that may be needed for application logic.
Additional Benefits
Caveats
- The more bit flag entries that are added, the less benefit from a number of records standpoint - for each added entry, the number of records in the
combinations table doubles and more than doubles in the associated bridging table. The tipping point for adding more entries will need to be determined for each specific use case. - Referential integrity does not keep an item from being added to the
Combinations table that is not valid per the contents of the Bit Flag table.
- Resolution: Add an
INSERT trigger to the Combinations table to perform the validation and cancel the insert if it is invalid.
Conclusion
Given the right use case, it is possible to incorporate the use of bit flags into the database design in a way that can better support application developers, enforce referential integrity, potentially reduce record count, provide some specific performance advantages and definitely increase flexibility in providing more options.
I see this as an additional tool and pattern for the database design arsenal. It can be helpful to include in some database designs, though is certainly NOT the answer for all many-to-many relationship data architecture problems. It can potentially be beneficial for some scenarios where lists are used in many-to-many configurations, the shorter and more static the list, the better. If you think you might like to try this pattern, my recommendation is: do your due diligence, weigh everything carefully, especially the implications of future growth, and be sure not to (en)code yourself into a corner!
Have Fun OR ( | ) Happy (En)coding!

History
- 14th July, 2017: Initial draft
- 26th July, 2017: Submitted for review
