Introduction
In the CodeProject's programming lounge and other discussion forums, inquirers often post technical questions wondering about an algorithm and the specific code written in Visual Basic .NET and other programming languages that allows to quickly and easily parse various mathematical expressions. In the most cases the requirement for this code assignment is that a mathematical expression must be a string of characters containing numbers, arithmetic operators and parentheses. Also, acording to this assignment, at the end of performing the actual parsing we must obtain the resulting numerical value of the expression being parsed.
Since that, the problem being addressed can be successfully solved by using the number of currently existing algorithms. Specifically, the famous "Polish notation" proposed by polish logician Jan Lukasiewicz in 1924 is the very first and the most appropriate algorithm for parsing complex mathematical expressions containing parentheses used to define the precedence of arithmetic operators order.
While using the Polish notation algorithm we're actually aiming to evaluate the resulting output value of the expression being parsed by performing arithmetic operations on the specific operand values with respect to the normal order as well as its modifications denoted by the parentheses. For example, (5 + 7 * 9) / 2 = 34. 7 * 9 => 63 + 5 = 68 / 2 => 34. In this case, 7 * 9 = 63 and 5 + 63 are evaluated first since the (5 + 7 * 9) is enclosed by the parentheses.
The following algorithm is mainly based on the idea of using two separate priority stacks for either operators or their operands and is formulated in two basic variants of either "Polish notation" (PN) or reverse "Polish notation" (RPN) respectively. The first variant of Polish notation algorithm is also called a "prefix notation" in which operators have a higher precedence rather than their operands. In fact, the difference between these two variants is that the second variant uses the "postfix notation" according to which the operands must have a higher precedence rather than the specific operators.
The "Polish notation" algorithm has the number of known applications such as either digital calculators, CPU's arithmetical logic units (ALU), various compilers and interpreters or even legacy aircraft navigation devices.
Background
In this article, we'll discuss about one of the most popular and obvious implementations of the mathematical expressions parser which unlike the conventional Polish notation algorithm does not require a separate stacks for both operators and operands to be used. In contrast, we'll use a single array in which the operands and operators are stored in their initial order. Also, we'll use the "prefix notation" variant since we're about to evaluate the expressions in which the several parts of an expression are enclosed by the number of one or more nested parentheses.
Basically, according to the algorithm being formulated, the actual parsing is typically performed in two main phases. During the first phase we'll typically need to locate all those parts enclosed by the parentheses in the expression being parsed. The location process will occur by performing a simple linear search starting at the position of the part enclosed by the innermost parentheses. We will recursively proceed with the following process until we've found all parts and inserted them into an array without parentheses. By performing the second phase, we'll actually compute the value of each particular part and substitute it into all other parts in the array, so that the computed value of the last part is the resulting value of the entire expression being evaluated.
Parsing the mathematical expression
As we've already discussed, during the first phase of the algorithm being discussed, we actually have to parse a an input string, in which the following expression is represented lexicographically. The numerical values in the expression being parsed are provided as traits of decimal digit characters ('0'-'9')<font>.</font> Respectively, the arithmetic operators are specified by using ('+', '-', '*', '/') group of characters. The parentheses are typed in by using the pair of either '(' or ')' corresponding characters.
Since we have a string containing a mathematical expression passed as an input parameter, we will perform a trivial linear search in the given input string to find the '(' character corresponding to the innermost opening parenthesis in the expression being parsed. To do that, we actually need to iterate through the given input string starting at the position of the last character in string and for each particular character perform a test if the current character is equal to '('. If so, we're performing the series of loop iterations to step forward through all succeeding characters until we've found the first occurrence of ') matching character located at a certain position in the string being traversed. In this case, during each iteration we're actually copying each character we've stepped into to a specific location starting at the first position in the previously allocated string buffer, so that at the end of performing those iterations the following buffer would contain the fragment of the input string located between two parenthesis of either '(' or ')'. This process being discussed is typically called a "substring extraction". After we've obtained a fragment of string containing the innermost part of the expression, we also must to do two more things.
The first thing is that we must to avoid the duplication of finding the character ')' at the same position in the input string being parsed. For example, suppose that, by performing a linear search we've already found the character '(' at the position corresponding to the value of index loop counter variable equal to (i == 17). After that we're performing series of loop iterations during which we're incrementing the value another loop counter variable j starting at (j = i + 1) until we've found the ')' parenthesis character at the position (j == 23). Since the matching ')' was found and the previously allocated string buffer already contains the innermost part of the expression, we're proceeding with those iterations by stepping backward through all remaining characters until we've stepped into another '(' character located at the position (i == 5). At this point we perform the series of iterations stepping into each character forward over again and occassionally locate the ')' character at the same position (j == 23) that was already been located. This normally incurs the extraction of an improper part of the expression being parsed.
To avoid the case when the ')' character is found for more than once, we actually need to allocate and use an array of ')' character positions, so that everytime when we've found the position of a closing parenthsis ')' we have to perform a check if the following position is not in the array of positions (e.g. has never been found before). If so, we simply have to break the loop execution since the string buffer is already assigned to all characters of the proper fragment of string containing the innermost part of the expression. Otherwise we must continue with the loop iterations stepping forward and bypassing a character ')' at the current position in string, which value is already contained in the array of positions.
After we've extracted a proper substring containing the innermost part of the expression, we must add the value of ')' character position to the array of positions, assuming that the character ')' was already parsed at its current position. Fig 1. illustrates the process of finding all those expression's fragments:
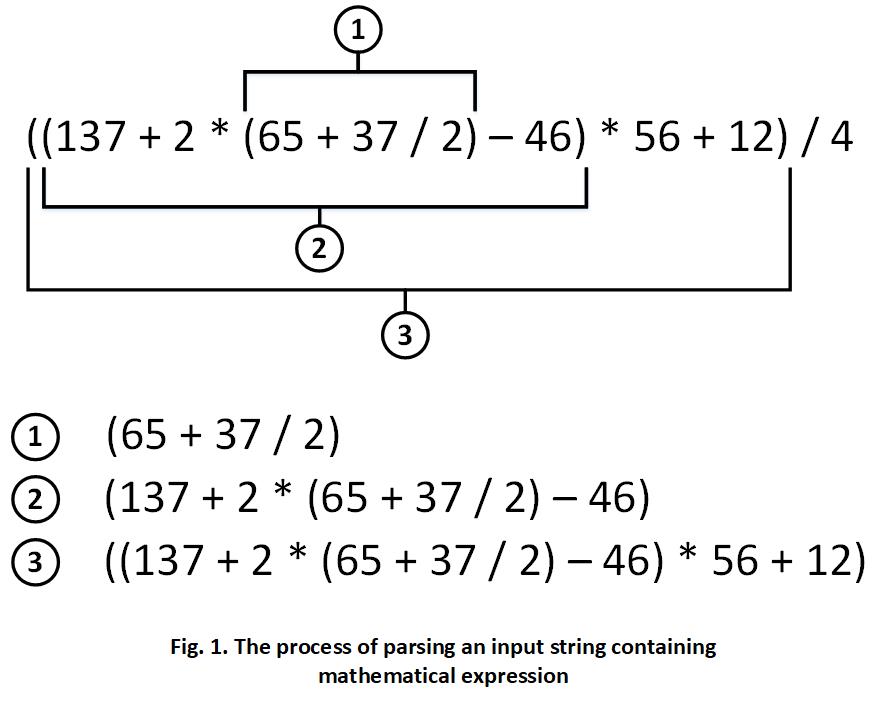
Another thing that we're intended to do is to add the following fragment to the array of expression parts as it's shown on Fig 1. To do this, we normally need to allocate a specific buffer prior to the process of actual parsing. To add an expression part to the array, we need to assign it at the position specified by a particular loop counter variable. After we've assigned the expression part at a specific location in the array, we increment the value of that loop counter variable to obtain the value of the next position at which we'll be assigning the next part of the expression.
Let's remind that, all parts of the expression in the array are ordered by their actual precedence. The first part in the array has the highest precedence, while the last one - the lowest. It actually means that we will be evaluating each part of the expression in its normal order the way it's typically done by a human. During the second algorithm's phase we'll evaluate the first part to obtain its value. Then, we'll substitute the result to all succeeding parts in the array. After that, we'll proceed with the next part and so on.
Evaluating The Expression Without Parentheses
During the second phase of the algorithm being discussed we'll evaluate the result of the entire expression being parsed by obtaining the resulting value of each part in the array of expressions. Before we begin the discussion of the second phase, let's spend a moment and take a closer look at the process during which we're actually obtaining the resulting value of the current expression in the array.
As we already know, we've basically dealt with specific parts of the entire expression in a string format. Obviously that, to evaluate each expression in the array we must implement an "interpreter" that allows us to obtain the numerical resulting value based on the specific input string containing numerical values and specific arithmetic operators.
To do this, we use a trivial linear search algorithm according to which we're performing the number of loop iterations to step forward through all characters in the input string starting at the position of the first character (i = 0). For each character located at the position that corresponds to the value of loop counter variable i being incremented, we must verify if the current character is a digit ('0'-'9'). If so, we need to perform the iterations of another loop stepping into each succeeding character starting at the position j = i + 1 until we've found a non-digit character. While executing the iterations of the following loop we're actually copying each of those suceeding characters to the previously allocated temporary string buffer, so that at the end of this loop execution the string buffer will contain a sequence of digits of a particular numerical value. Then, we'll add this numerical value to the string array being previously allocated. Otherwise, if the current character is an arithmetic operator ('+', '-', '*', '/') we simply add the string having length equal to 1 containg this character to the same previously allocated array of strings as it's shown on Fig 2:

Before we proceed with the discussion of the second algorithm's phase, let's recall that in this case we've basically dealt with the prefix notation in which operators have a higher priority rather than their operands. Since we've already obtained an array of strings containing the either numerical values or arithmetic operators in their original order, we have to perform the same linear search in the following array to find each arithmetic operator and its operands. Actually, the process during which we compute the expression's resulting value is performed in two passes. During the first pass we're aiming to find each of those two multiplication ('*') and division ('/') operators since they have a higher precedence over the either addition ('+') or subtraction ('-') operators.
To do this, we normally perform the loop iterations and for each item in the array of strings with index i from 0 to N verify if the following item is a string containing one of those operators ('*') or ('/') respectively. If so, we need to retrive a pair of either previous (i - 1) or next (i + 1) strings in the array. For example, supposed we've already located a string containing the ('*') operator at the position (i == 3). Then we must retrive a pair of strings containing its operands at the positions of (i == 2) and (i == 4) respectively. In this case the first opeand op1 is equal to 2 and the second operand op2 is equal to 83. After we've obtained the current opertor and its operands we convert these string values into numerical and perform multiplication of these operands assigning the resulting value to the temporary variable. Then we need to remove all those three items { s2, s3, s4 } from the array and substitute them with a string containing that numerical resulting value as it's shown on Fig 3:

We repeate the procedure described above until the following array of strings no longer contains any of ('*') and ('/') operators.
During the second pass we actually do the exactly same, but, with one difference that we're performing a linear search to find all occurrences of ('+') , ('-') arithmetic operators as well as their operands. Similarly to what we've done before, we perform the addition and substraction of particular operand values until we've finally obtained the resulting value of the current expression in the array.
Actually, by performing the array of expression's parts traversal we normally apply the same computational approach to each part of the expression. Also, to finally obtain the resulting value of the entire expression without parentheses we must update all succeeding parts by substituting the resulting value of the current part to each of the succeeding part in the array.
To do that, we actually need to perform the loop iterations stepping into each particular part of the expression. In turn, as we've already mentioned above, we'll compute the resulting value of the current expression's part and update the rest of the succeeding expression's parts by performing another loop iterations and stepping through each succeeding expression replacing the substring containing the current expression's part with its resulting value without parentheses. Actually we must proceed with the following process until we've computed the resulting value of the last part of the entire expression located at the final position in the array of expression's parts. Fig. 4. illustrates the following process:

Since we've computed the resulting value of each part of the expression and substituted it into all other parts by using the algorithm thoroughly discussed above, the last part of the expression in the array can be easily evaluated to the resulting value of the entire expression without parentheses by performing the discussed above computations.
Using the code
This routine perform the actual parsing of an input string containing the mathematical expression typed from the keyboard:
Function Parse(input As String)
Dim t As Int32 = 0
Dim oe(0) As Int32
Dim strings As List(Of String) = New List(Of String)
For index = input.Length() - 1 To 0 Step -1
If input(index) = "(" Or index = 0 Then
Dim sb As String = ""
Dim n As Int32 = 0
If index = 0 Then
n = index
Else n = index + 1
End If
Dim exists As Boolean = False
Do
exists = False
Dim bracket As Boolean = False
While n < input.Length() And bracket = False
If input(n) <> ")" Then
sb += input(n)
Else bracket = True
End If
n = n + 1
End While
If exists <> True Then
Dim r As Int32 = 0
While r < oe.Count() And exists = False
If oe(r) = n Then
exists = True
sb += ") "
n = n + 1
End If
r = r + 1
End While
End If
Loop While exists = True
If exists = False Then
Array.Resize(oe, oe.Length + 1)
oe(t) = n
t = t + 1
End If
strings.Add(sb)
End If
Next
For index = 0 To strings.Count() - 1 Step 1
Dim Result As String = Compute(strings.Item(index)).ToString()
For n = index To strings.Count() - 1 Step 1
strings(n) = strings.ElementAt(n).Replace("(" + strings.Item(index) + ")", Result)
Next
Next
Return Compute(strings.Item(strings.Count() - 1))
End Function
By calling the following routine we perform the actual computation of the resulting value without parentheses of each part of the expression being parsed:
Function Compute(expr As String)
Dim Result As Int32 = 0
Dim val As String = ""
Dim op() As String = {"+", "-", "*", "/"}
Dim strings As List(Of String) = New List(Of String)
For index = 0 To expr.Length() - 1 Step 1
If IsNumeric(expr(index)) Then
val = Nothing
Dim done As Boolean = False
While index < expr.Length() And done = False
If IsNumeric(expr(index)) Then
val += expr(index)
index = index + 1
Else done = True
End If
End While
strings.Add(val)
ElseIf expr(index) = op(0) Then
strings.Add(op(0))
ElseIf expr(index) = op(1) Then
strings.Add(op(1))
ElseIf expr(index) = op(2) Then
strings.Add(op(2))
ElseIf expr(index) = op(3) Then
strings.Add(op(3))
End If
Next
Dim n As Int32 = 0
While strings.Contains("*") Or strings.Contains("/")
Dim found As Boolean = False
While n < strings.Count() And found = False
If strings(n) = op(2) Then
Dim op1 As Int32 = Integer.Parse(strings(n - 1))
Dim op2 As Int32 = Integer.Parse(strings(n + 1))
Dim Res = op1 * op2
strings.RemoveAt(n - 1)
strings(n - 1) = Res
strings.RemoveAt(n)
Result = Res
found = True
n = 0
End If
If strings(n) = op(3) Then
Dim op1 As Int32 = Integer.Parse(strings(n - 1))
Dim op2 As Int32 = Integer.Parse(strings(n + 1))
Dim Res = CInt(op1 / op2)
strings.RemoveAt(n - 1)
strings(n - 1) = Res
strings.RemoveAt(n)
Result = Res
found = True
n = 0
End If
n = n + 1
End While
End While
n = 0
While strings.Contains("+") Or strings.Contains("-")
Dim found As Boolean = False
While n < strings.Count() And found = False
If strings(n) = op(0) Then
Dim op1 As Int32 = Integer.Parse(strings(n - 1))
Dim op2 As Int32 = Integer.Parse(strings(n + 1))
Dim Res = op1 + op2
strings.RemoveAt(n - 1)
strings(n - 1) = Res
strings.RemoveAt(n)
Result = Res
found = True
n = 0
End If
If strings(n) = op(1) Then
Dim op1 As Int32 = Integer.Parse(strings(n - 1))
Dim op2 As Int32 = Integer.Parse(strings(n + 1))
Dim Res = op1 - op2
strings.RemoveAt(n - 1)
strings(n - 1) = Res
strings.RemoveAt(n)
Result = Res
found = True
n = 0
End If
n = n + 1
End While
End While
Return Result
End Function
Points of Interest
In this article we've discussed about the very basic approach for evaluating mathmatical expressions lexicographically represented as an input string of characters. Probably, someone would like to experiment, inventing and proposing the more sophisticated and at the same time more efficient algorithm intended to do exactly the same :) ......
History
- September 14, 2017 - The first revision of article was published
