This is the sixth in a series of articles demonstrating how to build a .NET AI library from scratch. In this article, we will learn about the main ML algorithms based on function or type of problems they solve. For the sake of simplicity and due to time constraints, only algorithms, concepts and final equations will be shown and no statistics or mathematical proofs shall be provided.
Series Introduction
Here are the links for previous articles in the series:
My objective is to create a simple AI library that covers a couple of advanced AI topics such as Genetic algorithms, ANN, Fuzzy logics and other evolutionary algorithms. The only challenge to complete this series would be having enough time to work on the code and articles.
Having the code itself might not be the main target, however, understanding these algorithms is. Wish it will be useful to someone someday.
Please feel free to comment and ask for any clarifications or hopefully suggest better approaches.
Article Introduction - Part 6 "ML Algorithms"
We have discussed types of ML (Machine Learning) in the second article(20) (Supervised, unsupervised & reinforced). This classification is based on “The learning approach” mainly. However, this is not enough to define the essence of “How” exactly learning is conducted.
Another classification for ML algorithms are based on the function there is, so far, we have introduced a couple of ML areas such as regression and classification. In this article, we are targeting main ML algorithms based on function or type of problems they solve.
As a note, for the sake of simplicity and due to time constraints, only algorithms, concepts and final equations will be shown and no statistics or mathematical proofs shall be provided.
What is ML Algorithm?
ML Algorithms are tools and techniques used to actually extract information for a given data set and/or detect patterns.
Why do we need these algorithms? Clearly, this shall satisfy the learning portion of AI as a concept.
In the following section, we will introduce Regression, Classification & Clustering.
1-Regression Algorithms
Quote:
Regression (10) is simply; to find the best-fit mapping (or relationship) between inputs and output(s)
It represents a very old statistical field of study with many analytical approaches that are developed based on type of regression.
Regression analysis is a form of predictive modelling technique, which investigates the relationship between a dependent (target or label) and independent variable (input or predictor). This technique is used for forecasting, time series modelling and finding the causal effect relationship between the variables.
Regression analysis is an important tool for modelling and analyzing data. Here, we fit a curve / line to the data points, in such a manner that the differences between the distances of data points from the curve or line is minimized.
Types of Regression Techniques
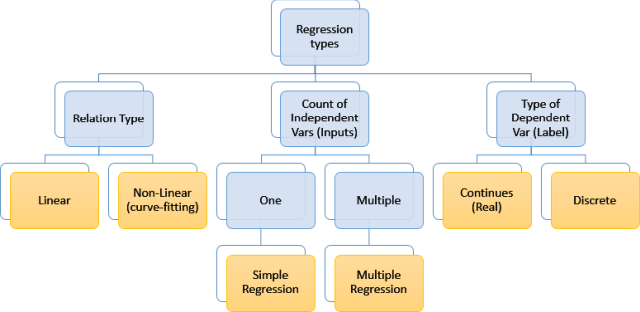
Relationship between a group of variables can fit different models, simplest is Linear model where straight line could be best-fit (in 2D space) or plane (in 3D space) or Hyperplane in higher-D spaces.

Linear regression (2D)


Non-Linear regression (2D)

Linear regression (3D)
The most popular regression algorithms are:
- Linear Regression
- Logistic Regression
- Ordinary Least Squares Regression (OLSR)
- Stepwise Regression
- Multivariate Adaptive Regression Splines (MARS)
- Locally Estimated Scatterplot Smoothing (LOESS)
2. Classification
Classification is a mapping function as well between X inputs and output(s) Y. Where Y is possible of classes.
If regression is finding best-fit line between inputs and output, classification is finding best-discrimination line that separates inputs to one or multiple classes.

If number of classes is two, it is called Binary classification.
If there are more classes, it’s called multiclass classification.
As regression, it provides a prediction means based on training data set, so classification belongs to Supervised ML approach.
Examples of classification algorithms:
- Linear classifiers
- Logistic regression
- Naive Bayes classifier
- Perceptron
- Support vector machines
- Quadratic classifiers
- k-nearest neighbor
- Decision trees
- Neural networks
- Learning vector quantization
3. Clustering
Clustering is grouping (similar to classification) but with no pre-defined labels (no classes). Clearly, it is part of unsupervised ML type of algorithms.
To group objects into different groups without having pre-defined classes, one way is to group based on distances or features. Actually, different clustering algorithms use different approaches.

In the above graph, objects (inputs) could be grouped into 3 (based on distance or other information within feature set).
There are three types of clustering based on similarity:
I. Exclusive clustering
One object belongs to one group only:

II. Overlapping clustering
Each object can belong to one group (cluster) or more:

III. Hierarchical clustering
It is more as tree-type relation. Two or more clusters may have parent clusters.

Types of Clustering Algorithms
Grouping objects could be based on different similarity measures on given inputs. Here are the most common similarity measures:
Connectivity Models (21)
AKA hierarchical clustering, approach is simple that; object is more related to near objects other than further ones in distance.
Centroid Models (22)
AKA K-Means clustering algorithm, it is a popular algorithm that, the no. of clusters required at the end have to be mentioned beforehand, which makes it important to have prior knowledge of the dataset. These models run iteratively to find the local optima.
Objects are grouped (clustered) based on distance from cluster centroid.

Distribution Models
These clustering models are based on the notion of how probable is it that all data points in the cluster belong to the same distribution (For example: Normal, Gaussian). A popular example of these models is Expectation-maximization algorithm which uses multivariate normal distributions.

Density Models
These models search the data space for areas of varied density of data points in the data space. It isolates various different density regions and assigns the data points within these regions in the same cluster. Popular examples of density models are DBSCAN and OPTICS.

Here is a summary of ML types:

Common ML Algorithms
1- Linear Regression
Linear regression, where a straight line (or plan or hyperplane) can be best-fit mapping between data set.
Data set is a sample of different input(s) data and associated labels (actual output) in such case, input is called Independent variable while output is called dependent variable
In cases where we have only one independent variable (input), known as Simple Linear regression however in case of more independent variables, this is called Multiple Linear Regression.
Linear Regression Parameters
To understand linear regression, we have to refer to mathematical representation, so for 2D mapping (relationship between variables) and simple linear regression, let’s denote dependent variable as Y and independent variable as X. For Y and X to have linear mapping, we need to figure out the equation of straight line that can fulfil this linearity. In other words, the mapping between Y & X shall be in form similar to:
Y = a + m * X

where:
a is the intercept Point (point where Y =0), known as bias coefficientm is the line slope (ration between change of Y to change of X), known as coefficient
In multiple linear regression where Y is dependent to multiple inputs, let’s say X1, X2,……. Xn equation shall be
Y = a + m1 * X1 + m2 * X2+ . . . . . . . . + mn * Xn
So, parameters are a and m (m1, m2, …. mn) Linear algorithm training is referring to find values for a & m that provide best-fit equation.
Different training algorithms are available to resolve parameters of linear regression, the most common are:
2- Simple Linear Regression
Y = a + m * X
Assume starting with any random parameters values, then at given sample i in data set, where we have Yi corresponding to Xi, we can define error at that sample as Ei where:
Ei = Yi – (estimated output)
Ei = Yi – (a + m * Xi)
Squaring this error is (Ei)^2 = (Yi – (a + m * Xi))^2
By summing all errors in all samples:

To find values of a & m that can minimize SE (Squared error), take the derivative with respect to a and m, set to 0, and solve for a and m. Explanation of mathematical formulas is beyond the scope of this article due to simplicity and time considerations. Finally, the Least Squared estimation for a & m is:


Further, sample Variance (11) and sample Covariance (12) are defined as:


So, m equation can be simplified to:

1- Calculate Average of inputs and Labels (Xavg & Yavg)
2- Calculate sample Covariance
3- Calculate sample Variance
4- Calculate m = Cov/Var
5- Calculate a= Yavg – m * Xavg
Logic
Created SimpleRegression Class
Public Class SimpleRegression
Public Shared Function LineBestFit(X_Inputs As Matrix1D, Y_Labels As Matrix1D) As Vector
Dim Line As New Vector
Dim X_avg As Double = 0
Dim Y_Avg As Double = 0
Dim Cov_XY As Double = 0
Dim Var_X As Double = 0
Dim X_Copy As New Matrix1D(X_Inputs)
Dim Y_Copy As New Matrix1D(Y_Labels)
X_avg = X_Inputs.Sum / X_Inputs.Size
Y_Avg = Y_Labels.Sum / Y_Labels.Size
X_Copy = X_Inputs.Sub(X_avg)
Y_Copy = Y_Labels.Sub(Y_Avg)
Cov_XY = X_Copy.Product(X_Copy, Y_Copy).Sum
Var_X = X_Copy.SquaredSum
Line.y = CSng(Cov_XY / Var_X)
Line.x = CSng(Y_Avg - Line.y * X_avg)
Return Line
End Function
Public Shared Function Validate(X_Inputs As Matrix1D, _
Y_Labels As Matrix1D, Line As Vector) As Single
Dim Err As New Matrix1D(Y_Labels)
Dim Y_Estimate As New Matrix1D(Y_Labels)
Y_Estimate = X_Inputs.Product(Line.y)
Y_Estimate = Y_Estimate.Add(Line.x)
Err = Y_Labels.Sub(Y_Estimate)
Return Err.SquaredSum / (2 * X_Inputs.Size)
End Function
End Class
Class has functions, LineBestFit and Validate
LineBestFit - provides a & m best fit valuesValidate - calculate MSE (Mean Square Error) as a measure of algorithm (best-fit) quality
To Test Algorithm, created simple form:

Simple Regression Test Form App
Algorithm Evaluation
To evaluate accuracy of algorithm MSE (Mean Square Error) is calculated, however in some references, another parameter may be used which is regression standard error or the residual standard error denoted as s where:

3- Ordinary Least Squares (OLS)
The concept is fairly simple and logical, denoting the error as distance between actual label (correct answer) and estimated output (based on initial line equation) then, this method squares all errors for all samples in data set and sums it to provide sum squared error same as simple regression but for multiple variables.
Linear algebra is used to resolve this model(13):


4- Gradient Descent In Linear Regression
Gradient descent is used to find a local minimum of a function and pseudo code is simple:
Gradient descent is already explained at article 2(14):

Descent Gradient
GD minimizes loss function or cost function using above Pseudo code however, it is not that simple, especially for non-linear functions. Here are some of GD:

Function normally has one global minimum but may have multiple local minimums and GD could be trapped in one of local minimums.
There are many types of gradient descent algorithm, based on data ingestion:
| Full Batch GD | Use whole data at once to compute the gradient |
| Stochastic GD | Take a sample from data set to compute the gradient |
On the basis of differentiation techniques:
| First order Differentiation GD | Use first order differentiation for cost function |
| Second order Differentiation GD | Use second order differentiation for cost function
|
Variants of Gradient Descent algorithms (here is a good reference for GD methods):
- Vanilla Gradient Descent
- Momentum
- Nesterov accelerated gradient
- Adagrad
- Adadelta
- RMSprop
- Adam
- AdaMax
- Nadam
Here are some of the methods.
I. Vanilla Gradient Descent
This is the simplest form of gradient descent technique. Vanilla means pure form without any adulteration. Its main feature is that we take small steps in the direction of the minima by taking gradient of the cost function.
Parameter_Update = learning_rate * gradient_of_parameters
Parameter_New_Value = Parameter_Old_Value - Update
Learning rate is a very important parameter and should be treated with care when choosing its value.

II. GD with Momentum
Here, we tweak the above algorithm in such a way that we pay heed to the prior step before taking the next step:
Parameter_Update = learning_rate * gradient_of_parameters
Velocity = Previous_update * momentum
Parameter_New_Value = Parameter_New_Value + Velocity – Parameter_Update
Here, update is the same as that of vanilla gradient descent. However, with a new term called velocity, which considers the previous update and a constant that, is called momentum.

III. Adaptive Subgradient (AdaGrad)
ADAGRAD uses adaptive technique to change learning rate. It allows different step sizes for different features. Normally used with Stochastic GD:
Grad_component = Previous_grad_component + (gradient * gradient)
Rate_change = Square_root(grad_component) + epsilon
Adapted_learning_rate = learning_rate * rate_change
Parameter_update = Adapted_learning_rate * gradient
Parameter_New_Value = Parameter_Old_Value – Parameter_update
In the above code, epsilon is a constant, which is used to keep rate of change of learning rate in check.
IV. ADAM
ADAM is one more adaptive technique which builds on adagrad and further reduces it downside. In other words, you can consider this as momentum + ADAGRAD.
Here’s a pseudocode.
Adapted_gradient = Previous_gradient + ((gradient – previous_gradient) * (1 – beta1))
Gradient_component = (gradient_change – previous_learning_rate)
Adapted_learning_rate = previous_learning_rate + (gradient_component * (1 – beta2))
Parameter_Update = adapted_learning_rate * adapted_gradient
Parameter_New_Value = Parameter_Old_Value – Parameter_Update
Here beta1 and beta2 are constants to keep changes in gradient and learning rate in check.
5- Bayesian Linear Regression
Bayesian linear regression is an approach to linear regression in which the statistical analysis is undertaken within the context of Bayesian inference. When the regression model has errors that have a normal distribution, and if a particular form of prior distribution is assumed, explicit results are available for the posterior probability distributions of the model's parameters.
6- Polynomial Regression
Polynomial regression is a form of regression analysis in which the relationship between the independent variable x and the dependent variable y is modelled as an nth degree polynomial in x.

nth degree polynomial can be expressed as:

The polynomial regression model:

This can be resolved in linear algebra approach (Matrix conversion):

Using Ordinary Least Squares estimation, it can be resolved as:

While using higher degree polynomial could get a lower error, it can result in overfitting as well if not carefully validated.
7- Stepwise Regression
This form of regression is used when we deal with multiple independent variables X. In this technique, the selection of independent variables is done with the help of an automatic process, which involves no human intervention.
The aim of this modeling technique is to maximize the prediction power with minimum number of predictor variables. It is one of the methods to handle higher dimensionality of data set.
For further information about this algorithm (17), see the attached PDF document.
8- Regularization
Regularization is a technique that minimizes the sum of squared error and also reduces the complexity of the model to override model overfitting. To explain regularization, let us explore the terms Overfitting and Underfitting.
Overfitting
This is when the model describes a random error or noise instead of the underlying relationship. Normally, this is when the model is very complex such as having too many parameters relative to the number of observations.
A model that has been overfitted has poor predictive performance, as it overreacts to minor fluctuations in the training data.

The green line represents an overfitted model and the black line represents a regularised model. While the green line best follows the training data, it is too dependent on it and it is likely to have a higher error rate on new unseen data, compared to the black line (16).
Underfitting
It occurs when model or machine learning algorithm cannot capture the underlying trend of the data. Underfitting would occur, for example, when fitting a linear model to non-linear data. Such a model would have poor predictive performance.

Two popular examples of regularization procedures for linear regression are:
- Lasso Regression: where Ordinary Least Squares is modified to also minimize the absolute sum of the coefficients (called L1 regularization).
- Ridge Regression: where Ordinary Least Squares is modified to also minimize the squared absolute sum of the coefficients (called L2 regularization).
These methods are effective to use when there is collinearity in your input values and ordinary least squares would overfit the training data.
9- Ridge Regression
Ridge Regression is a technique used when the data suffers from multicollinearity (independent variables are highly correlated). In multicollinearity, even though the least squares estimates (OLS) are unbiased; their variances are large which deviates the observed value far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors.
For Sum of squared error SSE:

Yi is label or correct answer.
F(x) is predicted or guessed value = Y.


Ridge regression performs ‘L2 regularization‘, i.e., it adds a factor of sum of squares of coefficients in the optimization objective. Hence, we need to introduce an additional term to the equation:
Objective = Residual_Sum_of_Squares + lambda * (sum_of_square_of_coefficients)

Here lambda is a shrink factor that is determined outside of the model (it is a tuning parameter) and it assigns a weight to how much we wish to penalize the sum of squared coefficients.
Here, lambda is the parameter, which balances the amount of emphasis given to minimizing RSS vs minimizing sum of square of coefficients. lambda can take various values:
lambda = 0:
The objective becomes the same as simple linear regression.
lambda = ∞:
The coefficients will be zero. Why? Because of infinite weightage on square of coefficients, anything less than zero will make the objective infinite.
0 < lambda < ∞:
The magnitude of lambda will decide the weightage given to different parts of objective.
The coefficients will be somewhere between 0 and ones for simple linear regression.
Any non-zero value would give values less than that of simple linear regression.
As the value of alpha increases, the model complexity reduces.
10- Lasso Regression
LASSO stands for Least Absolute Shrinkage and Selection Operator.
Lasso regression performs L1 regularization, i.e., it adds a factor of sum of absolute value of coefficients in the optimization objective. Thus, lasso regression optimizes the following:
Objective = SSE + lambda * (sum_of_absolute_value_of_coefficients)

Here, lambda works similar to that of ridge and provides a trade-off between balancing SSE and magnitude of coefficients. Like that of ridge, lambda can take various values:
lambda = 0: Same coefficients as simple linear regression
lambda = ∞: All coefficients zero (same logic as before)
0 < lambda < ∞: coefficients between 0 and that of simple linear regression

11- Logistic Regression
This machine learning technique is commonly used for binary classification problems, meaning those in which there are two possible outcomes (Yes or No) that are influenced by one or more explanatory variables. The algorithm estimates the probability of an outcome given a set of observed variables.
Logistic Regression is part of a larger class of algorithms known as Generalized Linear Model (GLM).


Logistics Regression (2D)

Logistics Regression (3D)
The logistic regression can be understood simply as finding the Beta parameters that best fit:

Hypothesis function used is in logistic form.

In such case, t is:

In matrix formation:

Hence, h(x) can be written as:

GD can be used to resolve values for Beta (Weights) Pseudo code can be simplified as:
For Single Classifier (one discrete output):
Initialize Random Weights
Initialize Learning_rate
Iterate from i=1 to m (m is number of samples in data set)
Calculate Sum_Of_Errors
Err(i) = h(x(i)) – Label(i)
Scale Err to Input Err=Err(i) * X(i)
Sum = Sum + Err(i)
End loop
Weight_New_Value = Weight_old_value - Sum * Learning_rate
Above code if for single classifier, incase multi-classifiers, n classes:
For Multi-Classes Classifiers:
Initialize Random Weights
Initialize Learning_rate
Iterate for all classes j = 1 to n (n is number of classes)
Sum = 0
Iterate from i=1 to m (m is number of samples in data set)
Calculate Sum_Of_Errors
Err(i) = h(x(i)) – Label(i)
Scale Err to Input Err=Err(i) * X(i)(j)
Sum = Sum + Err(i)
End Loop
Weight_New_Value(j) = Weight_old_value(j) - Sum * Learning_rate
End loop
12- K-means Clustering
This algorithm is interested to resolve clustering kind of problems, where you would have data set of inputs (features) but with no labels (correct answers). Therefore, this is Unsupervised learning algorithm.
K-Means Clustering received n features and classify into k classes. But How to determine if an input (feature) belongs to class A or B? This algorithm uses Euclidean Distance (18) as a classifier. Simply, if point is nearer to Class A mean then it belongs to A or otherwise.
Here is K-Means Clustering with 2D (2 features) and 3D (3 features):

K-Means Clustering with 2D (2 features)

K-Means Clustering with 3D (3 features)
K-Means Clustering Pseudo code:
Get Data set of n features and k classes
Initialize random k means (known as centroids) m1,m2, …… , mk
Loop until there is no more moves Euclidean distance and classify all points
Based on random means, calculate
For i = 1 to k
Replace mi with the mean of all of the samples for cluster i
End For
End Loop
13- K Nearest Neighbors – Classification
K nearest neighbors is a simple algorithm that stores all available cases and classifies new cases based on a similarity measure (distance functions). K is the number of neighbors to consider.

Algorithm
A point is classified by a majority vote of its neighbors (k), with the point being assigned to the class most common amongst its K nearest neighbors measured by a distance function. If K = 1, then the point is simply assigned to the class of its nearest neighbor.
Points of Interest
This article is a summary of common ML Algorithms, it is neither full or extensive detailed summary where there are tons of algorithms. Just focused on common types.
There could be a second part of this article.
Attached at top of this article is a PDF version of this article.
References
History
- 29th September, 2017: Initial version
