(Client-Side + Server-Side Node.JS) Web Application on Microsoft Azure
JavaScript (Client-Side Only)
Introduction
“I hate spam, and that's what happens when you let businesses onto the network.” - Jan Koum.
In this article we’ll discuss about the implementation of a simple anti-spam control based on the famous naïve Bayesian classification algorithm that can be actively used to locate and filter out those texts (E-Mail, SMS, …) from a local messages database that the most likely might contain spam or other unsolicited data.
Proposed by Jason Rennie and further improved by Paul Graham in 1998, Bayesian algorithm became one of the most famous AI machine learning-based classification algorithms that, at the meanwhile, is actively used in the most of existing anti-spam protection software hence it provides an efficient and reliable way to recognize potential spam and other unwanted content based on determining spamliness probability of each particular text message.
During the discussion, we’ll introduce the basic ideas of performing spam messages classification formulated as Bayesian algorithm such as the mathematical background of naïve Bayesian classification algorithm that basically relies on the main concepts formulated as famous Bayesian theorem. Specifically, we’ll discuss about the formulas that allow us to estimate the probability of spam for each message as well as its fragments (i.e. separate “words”) in the given training set, based on the hypothesis that a particular message can be a spam or legitimate. We’ll find out how to train the Bayesian model by using a pair of two input datasets consisting of “spam” and “ham” (not “spam”) messages. Each one of these datasets is an array of probabilistic patterns that we’re about to use during the algorithm’s learning phase.
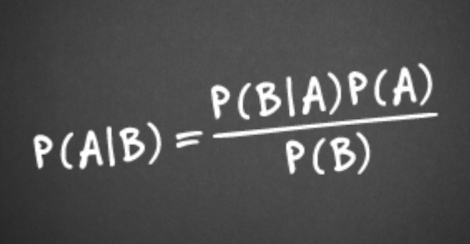
To compute the value of actual spam probability, we’ll use the total probability formula from the probability axiom that involves of using the trivial linear search algorithm to compute the statistics such as amounts of messages that exactly meet certain criteria of search.
Also, we’ll thoroughly discuss how to compute the value of overall spam probability of each message in case when the partial probability value of each word in a single message has already been computed. Simultaneously, we’ll make an emphasize on how to perform classification of messages from the entire training set by more than two distinct classes by using an improved probability computation formula.
Finally, we’ll provide useful guidelines on how to improve the efficiency of Bayesian algorithm by eliminating such issues as zero-frequency problem by adding “noise” and using Laplass k-adaptive smoothing.
After we’ve discussed above the naïve Bayesian classification algorithm intended to combat against spam and other unwanted data, we’ll demonstrate the wicked code written in HTML5 and JavaScript that implements a lightweight anti-spam filter web application sample that allows us to compute the spamliness probability of each message in the messages database based on using Bayesian classification algorithm.
Additionally, we’ll discuss on how to significantly improve the performance of code in JavaScript that performs the complex probability computations by using Parallel.JS framework.
At the end of this article, we’ll spend a bit more time to analyze and comment the spam prediction results provided by the web application being discussed.
Background
In this section, we’ll thoroughly discuss about the mathematical backgrounds and algorithm of the naïve Bayesian classifier as well as its application to reveal potential spam in a stack of text messages, that often arrives to our computers, tablets and cellphones as E-mail or SMS.
Naïve Bayesian Classification Algorithm Essentials
In today’s world, there is a vast of various opinions and strategies of solving the potential spam flood problem. As well, there’s even an entire class of computer algorithms addressing the solution of incoming spam and unwanted messages detection problem. The following class basically includes the either various AI machine learning algorithms that allow to perform spam detection based, for example, on the implementation of artificial neural networks trained to reveal spam messages by using the “experience” acquired from the continuous long-term learning process using database containing a huge number of spam messages. Those AI algorithms are typically complex and require large amounts of time to be trained for performing a quality spam prediction.
In fact, naïve Bayesian Classifier is a good example of an algorithm that inspired by the simplicity of probability theory, specifically Bayesian theorem, designed especially to solve the problem of fast and reliable spam detection based on the hypothesis that a certain message could be persistent among the either spam or legitimate messages.
Learning Process
The main reason why, the Bayesian data mining probabilistic algorithm belongs also to the class of AI algorithms is that it is the most suitable to deploy a simple process of machine learning during each “epoch” of which a large set of training messages already contained in the messages database so far is processed. Actually, the following algorithm allows to compute the spamliness probability of each particular message, that is further appended to either set of “spam” or “ham” (not spam) messages at the end of the spam probability value computation. After that, the spam detection engine proceeds with the probability computation for the next message retrieved from an input dataset, until it has determined the probability of spam for all existing messages. The similar process is performed for each new message that has just arrived at the messages database. The Bayesian algorithm learning process is illustrated on figure below:

As it’s shown above, naïve Bayesian classification algorithm uses three input datasets of messages. The first dataset contains only those messages recognized as “spam”. Respectively, the second dataset consists of messages that do not contain any spam fragments. Finally, the third dataset is a set of messages used for performing the actual Bayesian model training and includes messages for which we’re aiming to compute the spamliness probability. As we’ve already discussed each message from the third training dataset is classified and stored into the “spam” or “ham” datasets depending on the spam probability.
One of the most useful benefits of naïve Bayesian classification algorithm is that it uses the same probability computation procedure for either learning phase or the process of spam detection. This, in turn, makes the following algorithm an easy to formulate and implement. Hence we actually do not need two separate processes for either learning and detection phase, the using of the following algorithm allows to drastically accelerate the spam detection process.
Since we’ve already discussed about the Bayesian algorithm’s training scenario, let’s now delve into the explanation of the process of messages classification based on the performing the spamliness probability computation.
Initialization
The initialization phase for the algorithm being discussed is actually very simple. During this phase, all what we actually need is to assign the random initial probability value in the interval [-1;1] for each test message in the given dataset prior to performing the actual training. In fact, those initial random values being generated must be negligibly small preventing us from assigning the illegitimate values during the computation process and thus obtaining untrustworthy values of probability magnitude:

As we’ve already discussed, the using of Bayesian probabilistic model to compute the spam probability for messages containing “rare” words, which occurrence frequency is typically small, normally leads to obtaining the resulting value equal to 0 or NaN.
In the most cases, the following issue can be resolved by using an adaptive smoothing as well as providing an initial random probability value for each particular test message. In the other words, by assigning those initial random values we’re actually adding some “noise” to the probability computation process in order to avoid a case in which the probability magnitude prediction takes no effect and the following value for a particular test message still remains equal to 0 or NaN after performing those specific computations.
Spamliness of Words
Since we’ve performed the input dataset initialization for Bayesian prediction process, let’s spend a moment to understand the process of prediction itself. As we might already know from the very beginning, during the entire prediction process we’re aiming to compute the spam probability individually for each word in the given set of messages from the training dataset. This is typically done by using the following formula:

where: P(Word_i | Spam) – the probability that a specific word will occur at least in one of the spam messages;
P(Word_i | Ham) - the probability that a specific word will occur at least in one of the ham (“not spam”) messages;
P(Spam | Word_i) – the overall probability that a specific word is spam or a part of spam message;
The formula shown above is a special case of Bayesian theorem that allows to compute the probability of a certain event based on the condition of knowledge that another interrelated event has been realized. Also, the following formula is closely related to the law of total probability actively used in probability theory to relate the marginal to conditional probability magnitudes by expressing the value of total probability via the set of partial probabilities inherent to several distinct events.
There's the couple of approaches addressing a given word's spamliness probability computation. Specifically, we can compute the following probability values based on either messages- or words-based statistics. During the discussion we've basically dealt with both approaches of either messages- or separate words-based probability computation.
First, what we're about to discuss right at the very beginning is the messages-based statistics spam probability computation approach.
To compute the actual spamliness of a given word in a particular message based on the statistics of messages being collected, we normally need to compute the values of those two partial probabilities listed in the formula above. This is typically done by using the conventional formula that derives from the probability axiom:

where: Word_i - the given word for which spamliness probability value is computed,
P(Word_i | Spam) – the partial probability that Word_i is spam,
P(Word_i | Ham) – the partial probability that Word_i is ham (not spam!),
count(Word_i | Spam) the total amount of "spam" message containing Word_i,
count(Word_i | Ham) the total amount of "ham" message containing Word_i,
count(Spam) - the total amount of words in all spam messages,
count(Ham) - the total amount of words in all legitimate messages
In this case, to compute each of these probabilities mentioned above, we need to perform a trivial linear search in the either “spam” or “ham” messages datasets to estimate the number of messages containing the given word in the “spam” and “ham” training sets respectively. As well, we also need to compute the overall value of the number of messages in these datasets.
To obtain the probability value that given word is “spam” we’ve simply divided the number of messages in “spam” containing the given word by the total amount of messages belonging to the “spam” dataset. Similarly, we’ve divided the number of messages containing the given word in “ham” by the total number of “ham” messages to obtain the probability that the given word is “ham”.
Finally, we must substitute those probability values to the main formula listed above to obtain the measure of the spamliness of the given word.
As we've already discussed, to compute the spam probability for each given word, we'll use a slightly different formula shown below:

where: Word_i - the given word for which spamliness probability value is computed,
P(Word_i | Spam) – the partial probability that Word_i is spam,
P(Word_i | Ham) – the partial probability that Word_i is ham (not spam!),
count(Word_i) -> Spam - the total amount of Word_i in all spam messages,
count(Word_i) -> Ham - the total amount of Word_i in all ham (not spam!) messages,
count(Spam) - the total amount of words in all spam messages,
count(Ham) - the total amount of words in all legitimate messages
To find a given word's spamliness probabilty value based on the statistics of words, we must use the liniar search algorithm to compute the count of the occurrences of the following word in all messages containing spam, as well as the similar value of the occurrences count for the following words in all legitimate messages. After that, we need to simply divide these two values by the total number of words in either "spam" or "ham" messages to obtain the specific probability values that the given word belongs to "spam" and "ham" messages respectively.
According to the most of existing Bayesian spam classification algorithm guidelines, it's strongy recommended to use the value of the amount of distinct unique words in either all "spam" or "ham" messages. However, to provide an efficient performance optimization of the spam prediction process, we'll use the value of total possible amount of "spam"- or "ham"-words, since that the using of the total words count value does not have a sufficient impact on the specific probability values computation.
Computing Probability of Spam
Since, we’ve already found out how to compute the partial spamliness probabilities of each word within a single message, let’s take a closer look at the process of the total message spam probability computation.
Let's remind beforehand, that to compute the overall spam probability for a particular message based on the either messages- or words-based statistic, we'll use the same formula listed below.
As well as, for the particular words spamliness probability computation, there’s the number of methods by using which we can easily estimate the probability that a specific message in the given trainset actually contains spam.
The very first approach that provides the most trustworthy prediction results is to find the average value of the partial probabilities of each specific word in a given message. To do this we’ll use the following formula:

where: N - the amount of words in a given message,
P(Spam | Word_i) – the partial probability of spamliness,
p – the overall probability that a given message contains spam;
However, there're special cases when the following mathematical model fails to provide the correct values of spam probability. Specifically, for the words that rarely occur in given text the estimated value of probability might be equal to 0. To avoid the ocurrence of the following issues it's strongly recommended to use Laplass k-adaptive smoothing and add some "noise" to initial probability values during the initialization phase as we've already discussed right from the very beginning. Normally k-adaptive smoothing provides a very simple modification to the formula listed above:

Actually, to provide k-adaptive smoothing, we normally need to add up the value of 1.0 to the formula's numerator as well as the value of the overall number of distinct words to the formula's denominator respectively. This normally allows to avoid a case in which the value of total message's spam probability appears to be 0.
Is This A Spam Message?
Since we've already found out how to compute a probability of spam for each message in the given input training set, let's now take a shor glance at the process during which we'll use the probability data to detect spam in the new messages that arrive to the spam detection queue.
For that purpose we'll use the trivial liniar search algorithm and iterate through the array of the spamliness probability values that have already been previously computed for each particular word found in each message from the input training set.
To do this, we initially need to split up the input message string into an array of words. After that we're iterating through the following article and for each particular word from the input message string performing a linear search in the array of words spamliness probabilities to find the specific value of spam probability for the current word retrieved from the input message string. Since we've obtain the spamliness probability for the current word in the input message string, we're performing a check if the current word probability is greater than 0.5. If so, we're incrementing the value of spam words counter by 1. Otherwise, if the probability value is less than 0.5, then we're incrementing ham words counter by 1.
Finally, we're performing a check if the value of spam words counter is greater than the ham words counter value. If so, the current message contains spam, or is legitimate unless otherwise. Also, the value of message spam probability is computed as the division of the value of the number of spam words by the overall number of words within a given message.
Naїve Bayesian Anti-Spam Control Deployment Scenario
The using of AI machine learning and data mining algorithms normally provide the robust and efficient solution to combat agressive spam flood attacks. However, known software implementations of these algorithms basically require sufficient resources of CPU and system memory of regual PCs and servers that will perform the spam detection-specific tasks.
In this case, to provide the total anti-spam protection for PCs and mobile devices, it's strongly recommended to maintain a cluster of spam-protection servers, each one of which will serve as a cluster's node to accomplish the spam probability computation for the currently active incoming e-mail and SMS messages queue. The most common scenario for maintaining anti-spam protection cluster is shown on figure below:

According to the deployment scenario being introduced, we must maintain a computational cluster-based anti-spam protection cloud. Each computational node in the following cluster will perform a real-time background spam detection tasks for each message arrived to mailing servers over the Internet.
To provide a total anti-spam protection, mailing servers sent new messages arrived along with spam validation requests to the anti-spam protection cloud. Then, each particular message is sent to the internal anti-spam detection servers that perform the actual spam probability computation, and as the result respond with specific message status notifications received by those mailing servers. If the spam validation is passed, mailing servers store legitimate messages into messages database. Finally, those legitimate messages containing no spam are downloaded by e-mail client software installed on users PCs and other devices over the Internet.
In conclusion...
As we've already discussed there're a vast of various opinions and methods for fighting with potential spam arriving daily to our e-mail inboxes, SMS and chat-messangers. The Naїve Bayesian Spam Classification algorithm that has been introduced in this article is recommended solely for deploying an anti-spam solution discussed above. To maintain the front-end client anti-spam protection there're probably the other methods based on the other concepts rather than AI machine learning and data mining algorithms.
Using the code
In this section, we'll delve deep into the code written in JavaScript that implements a web application that performs the spamliness probability computation based on using Bayesian classification algorithm.
Loading Data
As we've already discussed, the testing dataset for this programming assignment is stored as a plain-text file:
The format is simple: A text file with 1 message per line, each line begins with "Spam" or "Ham" (ham is "not spam"), followed by a comma and then the message. The file is in 3 parts, each part labelled by a header starting with #. There's spam and ham messages for training, followed by a set of messages that are to be used for testing your code.
The following JavaScript code implements loading data from files uploaded to the web application:
Hide Shrink  Copy Code
Copy Code
var train_set = [];
var count_unique = [];
function loadData()
{
var file_reader = new FileReader();
var fp = document.getElementById("datafile_upload");
file_reader.onload = function() {
var data_set = new Array();
var contents = file_reader.result;
var lines_array = contents.split("#");
for (var i = 0; i < lines_array.length; i++)
{
if (lines_array[i].length > 0 && lines_array[i] != "")
{
var count = 0;
var data_ent = new Array();
var data_s = lines_array[i].split("\n");
for (var j = 0; j < data_s.length; j++)
{
if (data_s[j].indexOf("<p>") > -1) {
var words_raw = data_s[j].replace(new RegExp("<p>", 'g'), "")
.replace(new RegExp("</p>", 'g'), "");
if(words_raw.length > 0) {
var words = new Array(words_raw.split(" "));
for (var l = 0; l < words.length && i < 3; l++)
{
if (find_wds_n(words_raw, words[0][l]) == 1) {
count++;
}
}
data_ent.push({ "content" : words, "probability" : (Math.random() - Math.random()) / Math.pow(10,3) });
}
}
}
count_unique.push(count);
data_set.push(data_ent);
}
}
train_set = data_set;
renderData(2, train_set);
}
file_reader.readAsText(fp.files[0], "UTF-8");
}
Implementing Naive Bayesian Algorithm Using JavaScript and Parallel JS:
To compute the specific values of total probability, we'll need to obtain the value of the number of messages containing a given word. To do this, we'll need to count the number of word's occurrences in a particular message text. For that purpose, we've implemented the following JavaScript routine:
Hide Copy Code
function find_wds_n(text, word)
{
text += ''; word += '';
if (word.length <= 0) {
return text.length + 1;
}
word = word.replace(/[.*+?^${}()|[\]\\]/g, '\\$&');
return (text.match(new RegExp(word, 'gi')) || []).length;
}
To find the total number of messages containing the given word, we need to implement and use the following function:
Hide Copy Code
function find_msg_nw(tsID, data_set, word)
{
var msg_count = 0;
for (var i = 0; i < data_set[tsID].length; i++)
{
if (find_wds_n(data_set[tsID][i]["content"][0].toString(), word) > 0)
msg_count++;
}
return msg_count;
}
To compute the probability of a single message spamliness by using the formulas introduced above, we've implemented the following Javascript function:
Hide Copy Code
function predict_spam_wds(data_set, msg_index, count_spam, count_ham)
{
var p_spam = 1, p_ham = p_spam;
for (var i = 0; i < data_set[2][msg_index]["content"][0].length; i++)
{
var p_ws = find_msg_nw(0, data_set, data_set[2][msg_index]["content"][0][i]) / count_spam;
var p_wh = find_msg_nw(1, data_set, data_set[2][msg_index]["content"][0][i]) / count_ham;
var probability = ((p_ws + p_wh) != 0) ? p_ws / (p_ws + p_wh) : 0;
if (probability > 0) {
p_spam *= probability; p_ham *= 1 - probability;
}
}
return ((p_spam + p_ham != 0)) ? p_spam / (p_spam + p_ham) : 0;
}
To perform the actual Bayesian model learning by computing the spamliness probability for each particular message we've implemented the following fragment of code written in JavaScript and using Parallel JS framework to improve the performance of the following process:
Hide Shrink  Copy Code
Copy Code
function predict_all()
{
var p = new Parallel(Array.apply(null, { length : train_set[2].length }).map(Number.call, Number),
{ env: { data_set : train_set }, envNamespace: 'parallel' });
document.getElementById("status").innerHTML = "<p>Processing...</p>";
p.require(find_wds_n).require(find_wds_n)
.require(find_msg_nw).require(predict_spam_wds).map(function (data) {
return predict_spam_wds(global.parallel.data_set, data,
global.parallel.data_set[0].length, global.parallel.data_set[1].length);
}).then(function (data) {
for (var s = 0; s < arguments[0].length; s++)
{
train_set[2][s]["probability"] += arguments[0][s];
document.getElementById("entry" + s).innerHTML = "p = " +
train_set[2][s]["probability"].toString() + " R = [" + ((Math.round(train_set[2][s]["probability"]) > 0) ?
"<span style=\"color : red;\">Spam</span>" : "<span style=\"color : green;\">Ham</span>") + "]";
}
document.getElementById("status").innerHTML = "<p>Completed!!!</p>";
});
}
To render the data in the resulting set of messages, we've implementing the specific mechanism that performs the messages output by dynamically constructing a results web-page using DOM:
Hide Shrink  Copy Code
Copy Code
function renderData(tsID, data_set)
{
var ts_s = "<table border=\"1\" style=\"table-layout: fixed; overflow-x:auto; width: 100%;" +
"word-wrap: break-word;\"><thead><th width=\"1%\">#</th><th width=\"25%\">Message</th>";
if (tsID == 2) {
ts_s += "<th width=\"10%\">Statistics</th>";
}
ts_s += "</thead><tbody>\n";
for (var i = 0; i < data_set[tsID].length; i++)
{
if (tsID == 0 || tsID == 1) {
var words_s = data_set[tsID][i]["content"].toString();
ts_s += "<tr><td><center>" + i.toString() +
"</center></td><td>" + words_s.substr(0, 160) + "...</td></tr>\n";
}
else {
var words_s = data_set[tsID][i]["content"].toString();
ts_s += "<tr><td><center>" + i.toString() + "</center></td><td>" +
words_s.substr(0, 160) + "...</td><td><span id = \"entry" + i.toString() + "\">" +
"p = " + data_set[tsID][i]["probability"].toString() + "</span></td></tr>\n";
}
}
ts_s += "</tbody></table>";
if (ts_s.length > 0)
document.getElementById("train_set").innerHTML = ts_s;
}
The complete html-document containing the anti-spam control web-application is listed below:
index.html:
Hide Shrink  Copy Code
Copy Code
<!DOCTYPE html>
<html>
<head>
<script src="./parallel.js"></script>
<script src="http://ajax.googleapis.com/ajax/libs/jquery/1.9.1/jquery.min.js"></script>
<script src="http://hayageek.github.io/jQuery-Upload-File/4.0.11/jquery.uploadfile.min.js"></script>
<title>Naive Bayesian Anti-Spam Control v.1.0a</title>
</head>
<body>
<table border="1" style="width: 1200px;">
<tr>
<td align="center"><p style="font-size:30px;"><b>Naive Bayesian Anti-Spam Control v.1.0a<b></p></td>
</tr>
<tr>
<td>
<form>
<div>
<label for="datafile_upload">
<strong>Upload Data File (*.txt):</strong>
</label>
<input type="file" id="datafile_upload" accept=".txt" onchange="loadData();">
</div>
</form>
</td>
</tr>
<tr>
<td>
<table border="1">
<tr>
<td>
<table>
<tr>
<td><button onclick="renderData(2, train_set);">Test Data</button></td>
<td><button onclick="renderData(0, train_set);">Spam</button></td>
<td><button onclick="renderData(1, train_set);">Ham (Not "Spam")</button></td>
</tr>
</table>
</td>
</tr>
<tr>
<td>
<div id="train_set" style="width: 1200px; height: 500px; overflow-y: scroll;"></div>
</td>
</tr>
</table>
</td>
</tr>
<tr>
<td align="right">
<table>
<tr><td><span id="status"> </span></td><td><button onclick="predict_all();"><b>Predict</b></button></td></tr>
</table>
</td>
</tr>
<tr><td align="center"><b>CPOL (C) 2018 by Arthur V. Ratz</b></td></tr>
</table>
</body>
<script>
var train_set = [];
var count_unique = [];
function loadData()
{
var file_reader = new FileReader();
var fp = document.getElementById("datafile_upload");
file_reader.onload = function() {
var data_set = new Array();
var contents = file_reader.result;
var lines_array = contents.split("#");
for (var i = 0; i < lines_array.length; i++)
{
if (lines_array[i].length > 0 && lines_array[i] != "")
{
var count = 0;
var data_ent = new Array();
var data_s = lines_array[i].split("\n");
for (var j = 0; j < data_s.length; j++)
{
if (data_s[j].indexOf("<p>") > -1) {
var words_raw = data_s[j].replace(new RegExp("<p>", 'g'), "")
.replace(new RegExp("</p>", 'g'), "");
if(words_raw.length > 0) {
var words = new Array(words_raw.split(" "));
for (var l = 0; l < words.length && i < 3; l++)
{
if (find_wds_n(words_raw, words[0][l]) == 1) {
count++;
}
}
data_ent.push({ "content" : words, "probability" : (Math.random() - Math.random()) / Math.pow(10,3) });
}
}
}
count_unique.push(count);
data_set.push(data_ent);
}
}
train_set = data_set;
renderData(2, train_set);
}
file_reader.readAsText(fp.files[0], "UTF-8");
}
function find_wds_n(text, word)
{
text += ''; word += '';
if (word.length <= 0) {
return text.length + 1;
}
word = word.replace(/[.*+?^${}()|[\]\\]/g, '\\$&');
return (text.match(new RegExp(word, 'gi')) || []).length;
}
function find_msg_nw(tsID, data_set, word)
{
var msg_count = 0;
for (var i = 0; i < data_set[tsID].length; i++)
{
if (find_wds_n(data_set[tsID][i]["content"][0].toString(), word) > 0)
msg_count++;
}
return msg_count;
}
function predict_spam_wds(data_set, msg_index, count_spam, count_ham)
{
var p_spam = 1, p_ham = p_spam;
for (var i = 0; i < data_set[2][msg_index]["content"][0].length; i++)
{
var p_ws = find_msg_nw(0, data_set, data_set[2][msg_index]["content"][0][i]) / count_spam;
var p_wh = find_msg_nw(1, data_set, data_set[2][msg_index]["content"][0][i]) / count_ham;
var probability = ((p_ws + p_wh) != 0) ? p_ws / (p_ws + p_wh) : 0;
if (probability > 0) {
p_spam *= probability; p_ham *= 1 - probability;
}
}
return ((p_spam + p_ham != 0)) ? p_spam / (p_spam + p_ham) : 0;
}
function predict_all()
{
var p = new Parallel(Array.apply(null, { length : train_set[2].length }).map(Number.call, Number),
{ env: { data_set : train_set }, envNamespace: 'parallel' });
document.getElementById("status").innerHTML = "<p>Processing...</p>";
p.require(find_wds_n).require(find_wds_n)
.require(find_msg_nw).require(predict_spam_wds).map(function (data) {
return predict_spam_wds(global.parallel.data_set, data,
global.parallel.data_set[0].length, global.parallel.data_set[1].length);
}).then(function (data) {
for (var s = 0; s < arguments[0].length; s++)
{
train_set[2][s]["probability"] += arguments[0][s];
document.getElementById("entry" + s).innerHTML = "p = " +
train_set[2][s]["probability"].toString() + " R = [" + ((Math.round(train_set[2][s]["probability"]) > 0) ?
"<span style=\"color : red;\">Spam</span>" : "<span style=\"color : green;\">Ham</span>") + "]";
}
document.getElementById("status").innerHTML = "<p>Completed!!!</p>";
});
}
function renderData(tsID, data_set)
{
var ts_s = "<table border=\"1\" style=\"table-layout: fixed; overflow-x:auto; width: 100%;" +
"word-wrap: break-word;\"><thead><th width=\"1%\">#</th><th width=\"25%\">Message</th>";
if (tsID == 2) {
ts_s += "<th width=\"10%\">Statistics</th>";
}
ts_s += "</thead><tbody>\n";
for (var i = 0; i < data_set[tsID].length; i++)
{
if (tsID == 0 || tsID == 1) {
var words_s = data_set[tsID][i]["content"].toString();
ts_s += "<tr><td><center>" + i.toString() +
"</center></td><td>" + words_s.substr(0, 160) + "...</td></tr>\n";
}
else {
var words_s = data_set[tsID][i]["content"].toString();
ts_s += "<tr><td><center>" + i.toString() + "</center></td><td>" +
words_s.substr(0, 160) + "...</td><td><span id = \"entry" + i.toString() + "\">" +
"p = " + data_set[tsID][i]["probability"].toString() + "</span></td></tr>\n";
}
}
ts_s += "</tbody></table>";
if (ts_s.length > 0)
document.getElementById("train_set").innerHTML = ts_s;
}
</script>
</html>
Implementation Using Node.JS and Ajax Requests
index.pug:
doctype html
html
head
script(type='text/javascript').
var server_ip_addr = "http://localhost:1337/";
function loadData() {
var file_reader = new FileReader();
var fp = document.getElementById("datafile_upload");
file_reader.onload = function() {
var contents = file_reader.result;
document.getElementById("status").innerHTML = "Processing...";
var xhttp = new XMLHttpRequest();
xhttp.onreadystatechange = function() {
if (this.readyState == 4 && this.status == 200) {
var data = JSON.parse(this.responseText);
document.getElementById("train_set").innerHTML = data["result"];
document.getElementById("status").innerHTML = "Completed ( Took: " + data["exec_time"] + " ms )...";
}
}
xhttp.open("POST", server_ip_addr, true);
xhttp.send(JSON.stringify({ "action" : "loadData", "contents" : contents }, null, 3));
}
file_reader.readAsText(fp.files[0], "UTF-8");
}
function renderData(tsId) {
var xhttp = new XMLHttpRequest();
xhttp.onreadystatechange = function() {
if (this.readyState == 4 && this.status == 200) {
var data = JSON.parse(this.responseText);
document.getElementById("train_set").innerHTML = data["result"];
}
}
xhttp.open("POST", server_ip_addr, true);
xhttp.send(JSON.stringify({ "action" : "renderData", "ts_id" : tsId }, null, 3));
}
function Predict(msgText) {
var msgText = document.getElementById("input_msg").value;
var xhttp = new XMLHttpRequest();
xhttp.onreadystatechange = function() {
if (this.readyState == 4 && this.status == 200) {
var data = JSON.parse(this.responseText);
alert(data["result"]);
}
}
xhttp.open("POST", server_ip_addr, true);
xhttp.send(JSON.stringify({ "action" : "Predict", "msg_text" : msgText }, null, 3));
}
title Naive Bayesian Anti-Spam Control v.1.0a (Intro)
body
table(border='1', style='width: 1200px;')
tr
td(align='center')
p(style='font-size:30px;')
b Naive Bayesian Anti-Spam Control v.1.0a (Intro)
tr
td
form
div
label(for='datafile_upload')
strong Upload Data File (*.txt):
input#datafile_upload(type='file', accept='.txt', onchange='loadData();')
tr
td
table(border='1')
tr
td
table
tr
td
button(onclick='renderData(2);') Test Data
td
button(onclick='renderData(0);') Spam
td
button(onclick='renderData(1);') Ham (Not "Spam")
td
button(onclick='renderData(3);') Spamliness
tr
td
#train_set(style='width: 1200px; height: 500px; overflow-y: scroll;')
tr
td
table
tr
td
input#input_msg(type='text', value='', size='100')
button(onclick='Predict();') Is It A Spam?
tr
td(align='right')
table
tr
td
span#status
tr
td(align='center')
b CodeProject's CPOL(C)2018 by Arthur V. Ratz
server.js:
'use strict';
var url = require('url');
var path = require('path');
var http = require('http');
var debug = require('debug');
var logger = require('morgan');
var express = require('express');
var cluster = require('cluster');
var favicon = require('serve-favicon');
var bodyParser = require('body-parser');
var queryString = require('querystring');
var cookieParser = require('cookie-parser');
var port = process.env.PORT || 1337;
var numCPUs = require('os').cpus().length;
var w_count = 0, response = null;
var count_w_global = 0, data_set = [];
var workers = new Array();
if (cluster.isWorker) {
process.on('message', function (msg) {
var start = msg["start"], end = msg["end"];
var th_id = msg["th_id"], train_set = msg["train_set"];
var count_wds_global = msg["count_w_global"];
var count_spam = msg["count_spam"], count_ham = msg["count_ham"];
var ds = new Array(), vfreq = new Array();
for (var s = start; s < end; s++) {
var p_spam = 1, p_ham = p_spam;
for (var i = 0; i < train_set[2][s]["content"]["words"][0].length; i++) {
var p_ws = 0, spam_wds_cnt = 0;
for (var j = 0; j < train_set[0].length; j++) {
var text = train_set[0][j]["content"]["words"][0].toString() + '';
var word = train_set[2][s]["content"]["words"][0][i] + '';
word = word.replace(/[.*+?^${}()|[\]\\]/g, '\\$&');
var count = (text.match(new RegExp(word, 'gi')) || []).length;
if (count > 0) {
var exists = 0; p_ws++;
for (var n = 0; n < vfreq.length && !exists; n++) {
exists = (train_set[0][vfreq[n]["msg_index"]]["content"]
["words"][0][vfreq[n]["word_index"]] == word) ? 1 : 0;
}
if (exists == 0) {
spam_wds_cnt += count;
}
}
}
var p_wh = 0, ham_wds_cnt = 0;
for (var j = 0; j < train_set[1].length; j++) {
var text = train_set[1][j]["content"]["words"][0].toString() + '';
var word = train_set[2][s]["content"]["words"][0][i] + '';
word = word.replace(/[.*+?^${}()|[\]\\]/g, '\\$&');
var count = (text.match(new RegExp(word, 'gi')) || []).length;
if (count > 0) {
var exists = 0; p_wh++;
for (var n = 0; n < vfreq.length && !exists; n++) {
exists = (train_set[1][vfreq[n]["msg_index"]]["content"]
["words"][0][vfreq[n]["word_index"]] == word) ? 1 : 0;
}
if (exists == 0) {
ham_wds_cnt += count;
}
}
}
p_ws /= count_spam;
p_wh /= count_ham;
spam_wds_cnt /= count_wds_global;
ham_wds_cnt /= count_wds_global;
var probability = ((p_ws + p_wh) != 0) ? p_ws / (p_ws + p_wh) : 0;
var probability_wds = ((spam_wds_cnt + ham_wds_cnt) != 0) ?
spam_wds_cnt / (spam_wds_cnt + ham_wds_cnt) : 0;
if (probability > 0) {
p_spam *= probability; p_ham *= 1 - probability;
}
if (probability_wds != 0) {
var exists = 0;
for (var q = 0; q < vfreq.length && !exists; q++) {
exists = (train_set[2][s]["content"]["words"][0][i] == train_set[2][vfreq[q]
["msg_index"]]["content"]["words"][0][vfreq[q]["word_index"]]) ? 1 : 0;
}
if (exists == 0) {
vfreq.push({ "msg_index": s, "word_index": i, "freq_spam": probability_wds });
}
}
}
ds.push(((p_spam + p_ham) != 0) ? p_spam / (p_spam + p_ham) : 0);
}
process.send({ "th_id" : th_id, "start": start, "end": end, "ds": ds, "vfreq": vfreq });
});
}
if (!cluster.isWorker) {
var express = require('express');
var cons = require('consolidate');
var app = express();
app.engine('html', cons.swig);
app.set('view engine', 'pug');
app.get('/', function (req, res) {
res.render('index.pug', {
title: 'Naive Bayesian Anti-Spam Control v.1.0a (Intro)'
});
});
app.listen(443);
http.createServer(function (req, res) {
res.setHeader('Content-Type', 'application/json');
res.setHeader('Access-Control-Allow-Origin', '*');
res.setHeader('Access-Control-Allow-Credentials', true);
res.setHeader('Access-Control-Allow-Headers', 'X-Requested-With,content-type');
res.setHeader('Access-Control-Allow-Methods', 'GET, POST, OPTIONS, PUT, PATCH, DELETE');
var body = ''; response = res;
req.on('data', (chunk) => {
body += chunk;
}).on('end', () => {
if (body != "") {
var json_obj = JSON.parse(body);
if (json_obj["action"] == "loadData") {
parseData(json_obj["contents"]);
}
else if (json_obj["action"] == "renderData") {
response.end(JSON.stringify({ "result": renderData(json_obj["ts_id"], data_set) }, null, 3));
}
else if (json_obj["action"] == "Predict") {
response.end(JSON.stringify({ "result": Predict(json_obj["msg_text"]) }, null, 3));
}
}
else {
}
});
}).listen(port);
}
function parseData(contents)
{
var ds = new Array();
var lines_array = contents.split("#");
for (var i = 0; i < lines_array.length; i++) {
if (lines_array[i].length > 0 && lines_array[i] != "") {
var count = 0;
var data_ent = new Array();
var data_s = lines_array[i].split("\n");
for (var j = 0; j < data_s.length; j++) {
if (data_s[j].indexOf("<p>") > -1) {
var words_raw = data_s[j].replace(new RegExp("<p>", 'g'), "")
.replace(new RegExp("</p>", 'g'), "");
if (words_raw.length > 0) {
var words = new Array(words_raw.split(" "));
count_w_global += (i == 1 || i == 2) ? words[0].length : 0;
data_ent.push({
"content": {
"words": words, "wfreq": Array.apply(null,
new Array(words.length)).map(Number.prototype.valueOf, 0.00)
},
"probability": (Math.random() - Math.random()) / Math.pow(10, 3)
});
}
}
}
ds.push(data_ent);
}
}
data_set = ds; learn(data_set);
}
function renderData(tsID, ds) {
var ts_s = "";
if (tsID == 3 && ds[tsID] == null) {
alert("Train your model first!"); return;
}
if (tsID == 0 || tsID == 1 || tsID == 2) {
ts_s = "<table border=\"1\" style=\"table-layout: fixed; overflow-x:auto; width: 100%;" +
"word-wrap: break-word;\"><thead><th width=\"1%\">#</th><th width=\"25%\">Message</th>";
}
else {
ts_s = "<table border=\"1\" style=\"table-layout: fixed; overflow-x:auto; width: 100%;" +
"word-wrap: break-word;\"><thead><th width=\"5%\">#</th><th width=\"25%\">Word</th><th width=\"25%\">Spamliness</th>";
}
if (tsID == 2) {
ts_s += "<th width=\"10%\">Statistics</th>";
}
ts_s += "</thead><tbody>\n";
for (var i = 0; i < ds[tsID].length; i++) {
if (tsID == 0 || tsID == 1) {
var words_s = ds[tsID][i]["content"]["words"].toString();
ts_s += "<tr><td><center>" + i.toString() +
"</center></td><td>" + words_s.substr(0, 160) + "...</td></tr>\n";
}
else if (tsID == 2) {
var words_s = ds[tsID][i]["content"]["words"].toString();
ts_s += "<tr><td><center>" + i.toString() + "</center></td><td>" +
words_s.substr(0, 160) + "...</td><td><span id = \"entry" + i.toString() + "\">" +
"p = " + ds[tsID][i]["probability"].toString() + ((data_set[3] != null) ? (" R = [" +
((Math.round(ds[tsID][i]["probability"]) < 1) ? "<span style=\"color : green;\">Ham</span>" :
"<span style=\"color : red;\">Spam</span>") + "]") : "") + "</span></td></tr>\n";
}
else {
var probability = ds[tsID][i]["freq_spam"];
var msg_index = ds[tsID][i]["msg_index"], word_index = ds[tsID][i]["word_index"];
var word = ds[tsID - 1][msg_index]["content"]["words"][0][word_index];
ts_s += "<tr><td><center>" + i.toString() + "</center></td><td>" + word + "</td><td><span id = \"entry" + i.toString() + "\">" +
"p = " + probability.toString() + "</span></td></tr>\n";
}
}
ts_s += "</tbody></table>";
if (ts_s.length > 0)
return ts_s;
}
function learn(ds) {
data_set[3] = new Array(); var time_start = new Date();
var chunk_size = Math.ceil(ds[2].length / numCPUs);
for (var th_id = 0; th_id < numCPUs; th_id++) {
var worker = cluster.fork(); workers.push({ "worker": worker, "status" : 1 });
var start = (th_id * chunk_size) < ds[2].length ?
(th_id * chunk_size) : ds[2].length;
var end = ((th_id + 1) * chunk_size) < ds[2].length ?
((th_id + 1) * chunk_size) : ds[2].length;
workers[th_id]["worker"].send({
"th_id": th_id, "start": start, "end": end,
"train_set": ds, "count_spam": ds[0].length,
"count_ham": ds[1].length, "count_w_global": count_w_global
});
workers[th_id]["worker"].on('message', function (msg) {
workers[msg["th_id"]]["status"] = 0; w_count++;
data_set[3] = data_set[3].concat(msg["vfreq"]);
for (var i = msg["start"], n = 0; i < msg["end"]; i++, n++) {
data_set[2][i]["probability"] = msg["ds"][n];
}
if (w_count == numCPUs)
{
w_count = 0; var time_end = new Date();
response.end(JSON.stringify({
"result": renderData(2, data_set), "exec_time": Math.abs(time_start - time_end) }, null, 3));
}
});
}
}
function Predict(msg_text)
{
var words_target = msg_text.split(" ");
var spam_ws_p = 0, ham_ws_p = 0;
for (var i = 0; i < words_target.length; i++) {
var exists = 0, spam_wd_index = -1;
for (var j = 0; j < data_set[3].length && !exists; j++) {
var msg_index = data_set[3][j]["msg_index"];
var word_index = data_set[3][j]["word_index"];
var word = data_set[2][msg_index]["content"]["words"][0][word_index];
if (words_target[i] == word) {
exists = 1; spam_wd_index = j;
}
}
if (exists == 1) {
spam_ws_p = (data_set[3][spam_wd_index]["freq_spam"] > 0.5) ? spam_ws_p + 1 : spam_ws_p;
ham_ws_p = (data_set[3][spam_wd_index]["freq_spam"] <= 0.5) ? ham_ws_p + 1 : ham_ws_p;
}
}
var probability = (spam_ws_p != ham_ws_p) ? ((spam_ws_p > ham_ws_p) ?
spam_ws_p / words_target.length : (1 - ham_ws_p / words_target.length)) : 0.5;
var rs_s = "p = " + probability + " R = [" + ((spam_ws_p > ham_ws_p) ? "Spam" : "Ham") + " ]";
return rs_s;
}
Points of Interest
At the meanwhile there're many opinions regarding the question on how to perform the messages spamliness probability computation the most correctly. Specifically, the spam probability magnitude can be evaluated based on the either messages- or words-based statistics. These both approaches provide different results and quality of spam prediction. I hope that it will be rather interesting to survey the results obtained by using these both approaches, and, finally, select the approach capable of providing the desired quality of spamliness prediction.
History
- February 11, 2018 - The first revision of the article has been published;
- February 19, 2018 - The final revision of the article has been published;
