Introduction
Have you ever noticed how childish and imprecise your signature looks when you write your name in a handheld signature box? The small size of the stylus compared to a standard pen, the nearly frictionless stylus-on-touch-screen interaction and the fact that the handheld is often hanging in the air instead of firmly lying on a table are three physical explanations for these ugly signatures. Another reason is the frequent input errors that are sent to your control from the touch screen. Those errors may vary between 1 and 4 pixels. Unnoticeable when clicking in the middle of a button, they are a pest when sampled in a signature box. By lowering the sampling rate and using Bézier curve interpolation, it's possible to reduce the impact of all these factors.
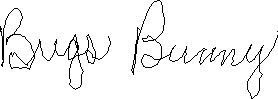
Without Bézier interpolation, the signature looks clumsy
| 
Using Bézier interpolation, most sampling errors are corrected
|
Background
While working on a project, a customer asked me to add a signature input box to his application. I looked around the Web to find an open source implementation of such a control and could not find any of sufficient quality. In the end, I decided to create my own and by the way, improving the concept using Bézier curves just to see how better the result could look. Making it open source was just natural to me. The project can now be found at SourceForge.net.
Bézier curves are used in many computer graphic applications. For example, true type fonts use cubic Bézier splines to render smooth character curves. Bézier interpolation is also used in 3D graphic animations to render smooth and natural movements. When used to smooth long and complex curves, it's better to use a Bézier path, which is a spline computed at every four points instead of the entire point set. Usage of cubic spline on a point set of four points is much faster than using the general Bézier recursive algorithm for the same result. Cubic spline, quadratic spline and linear interpolation are respectively used with samples of four, three and two points. When a sample contains more than four points, it becomes easier to use the general Bézier curve algorithm. For mathematical background and examples on Bézier curve, see the Wikipedia article. Animated GIFs and explanations given there are a good start on the subject.
Using the Code
Usage of the SignatureBox control is quite simple and straightforward. Just add the signature box to your application and make it appear the shape you want. The CreateImage method creates an image from the sampled points whether using Bézier or not (depending on the IsBezierEnabled property value). The Clear method is used to erase the content of the SignatureBox. So simple that there is nothing more to say about that control. That's why I'll expand on how I reduced the sampling rate of the control and how my Bézier implementation works in the next two sections.
Reducing the Sampling Rate
The algorithm judges if the current point is to be kept depending on its distance from the last point sampled using the pictureBox_MouseDown, pictureBox_MouseMouve and the pictureBox_MouseUp events. Upon pictureBox_MouseDown, the point given by the MouseEventArgs is added to the internal point list and set to the lastPoint field. On every pictureBox_MouseMove, the distance between the current point and the lastPoint is computed and if it's larger than the internal constant SAMPLING_INTERVAL, the point is kept. Then, when the pictureBox_MouseUp event occurs, a Point.Empty is added to the internal point list and set to the lastPoint field. The Point.Empty value is then interpreted by the drawing algorithm to reproduce the moment when the pen left the surface of the touch screen.
Now let's see how it's done in the code:
private const float SAMPLING_INTERVAL = 1.5f;
private List<Point> points;
private Point lastPoint;
private void pictureBox_MouseDown(object sender, MouseEventArgs e)
{
this.lastPoint = new Point(e.X, e.Y);
this.points.Add(this.lastPoint);
}
private void pictureBox_MouseMove(object sender, MouseEventArgs e)
{
Point newPoint = new Point(e.X, e.Y);
if (Graph.Distance(this.lastPoint, newPoint) > SAMPLING_INTERVAL)
{
this.Draw(newPoint);
this.lastPoint = newPoint;
this.pictureBox.Refresh();
}
}
private void pictureBox_MouseUp(object sender, MouseEventArgs e)
{
this.StopDraw();
}
private void StopDraw()
{
if (this.bezierEnabled)
{
if ((this.pointCount > 0) && (this.pointCount < 4))
{
Point[] p = new Point[this.pointCount];
for (int i = 0; i < this.pointCount; i++)
p[i] = this.points[this.points.Count - this.pointCount + i];
this.graphics.DrawLines(this.pen, p);
}
}
this.lastPoint = Point.Empty;
this.points.Add(Point.Empty);
this.pointCount = 0;
}
Graph.Distance is a simple distance calculation:
public static double Distance(Point a, Point b)
{
return Math.Sqrt(Math.Pow(b.X - a.X, 2) + Math.Pow(b.Y - a.Y, 2));
}
With a distance of 1.5, it means that a point will be sampled only if it is at least 1.5 pixels away from the last sampled point. The following table shows how the pixels are sampled. Each box represents a pixel and contains the distance from the middle point which is the last point sampled:
Sampling demonstration
| 2.83 | 2.24 | 2.00 | 2.24 | 2.83 |
| 2.24 | 1.41 | 1.00 | 1.41 | 2.24 |
| 2.00 | 1.00 | 0.00 | 1.00 | 2.00 |
| 2.24 | 1.41 | 1.00 | 1.41 | 2.24 |
| 2.83 | 2.24 | 2.00 | 2.24 | 2.83 |
Bézier Général Algorithm
The general Bézier recursive algorithm is very simple. To have an idea how the recursion work, have a look at this animation from Wikipedia.org. There are five points for a total of four grey initial segments.
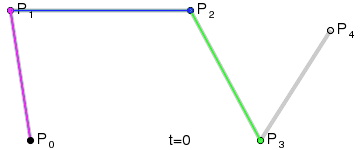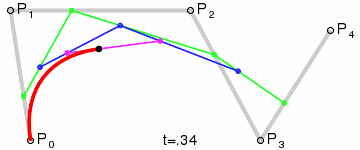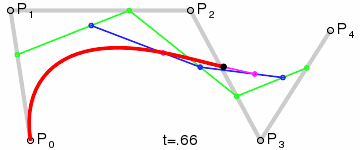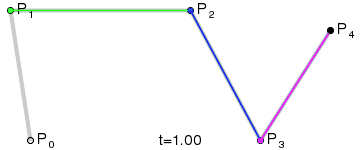
Bézier in action, courtesy of Wikipedia.org
For each segment in the point set, a new point is computed using linear interpolation at a fraction "t" which is between 0 and 1. This operation reduces the point set by one thus reducing the number of segments by one. The operation is repeated until the algorithm is called with only two points (see the magenta segment from the above GIF animation). At this moment, instead of calling the Bezier.Interpolate method another time, the last point is linearly interpolated from the last segment and is returned. To determine the precision of the algorithm and to draw the complete curve, repeat the Bézier interpolation "n" times for which "t = 1 / n".
My explanation is rather crude and may not be as mathematically exact as we were taught during undergraduate degree. I hope my code is clear enough to remove the fog I may have created with my explanations.
using System;
using System.Collections.Generic;
using System.Drawing;
using System.Text;
namespace GravelInnovation.BezierSignature
{
public static class Bezier
{
public static Point[] Interpolate(int nbPoints, PointF[] points)
{
float step = 1.0f / (nbPoints - 1);
Point[] retPoints = new Point[nbPoints];
int i = 0;
for (float t = 0; t < 1.0f; t += step)
{
PointF interpolatedPoint = InterpolatePoint(t, points)[0];
retPoints[i] = new Point(
(int)Math.Round(interpolatedPoint.X),
(int)Math.Round(interpolatedPoint.Y));
i++;
}
PointF lastPoint = points[points.Length - 1];
retPoints[retPoints.Length - 1] = new Point(
(int)lastPoint.X,
(int)lastPoint.Y);
return retPoints;
}
private static PointF[] InterpolatePoint(float t, params PointF[] points)
{
if (points.Length == 2)
return new PointF[] {new PointF(
t * (points[1].X - points[0].X) + points[0].X,
t * (points[1].Y - points[0].Y) + points[0].Y)};
PointF[] newPoints = new PointF[points.Length - 1];
for (int i = 0; i < points.Length - 1; i++)
newPoints[i] = InterpolatePoint(t, points[i], points[i + 1])[0];
return InterpolatePoint(t, newPoints);
}
}
}
Remark that instead of calling InterpolatePoint with "t" and two points to compute a linear interpolation, I should have created a private static Point LinearInterpolate(double t, Point p1, Point p2) method to make the whole code clearer. It's also clear that calling a recursive algorithm to resolve a third degree problem is overkill and less effective than using a cubic spline. Given the case of a signature, the overhead is not noticeable because there is only one point array. When used to smooth the movement of a 3D animation with thousands of point arrays themselves composed of thousands of points, any speed improvement in the algorithm is welcome.
Points of Interest
Using Bézier path improves significantly the quality of the signature without slowing too much the drawing rate on the control. If the functionality is unwanted, it's possible to set it off by changing the boolean property IsBezierEnabled.
History
- 16th February, 2011: Initial post
- 22nd February, 2011: Added code segments and a lot of explanations
