Introduction
Dijkstra's algorithm, named after its discoverer, Dutch computer scientist Edsger Dijkstra, is a greedy algorithm that solves the single-source shortest path problem for a directed graph with non negative edge weights. For example, if the vertices (nodes) of the graph represent cities and edge weights represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can be used to find the shortest route between two cities. Also, this algorithm can be used for shortest path to destination in traffic network.
Using the Code
I will explain this algorithm over an example.
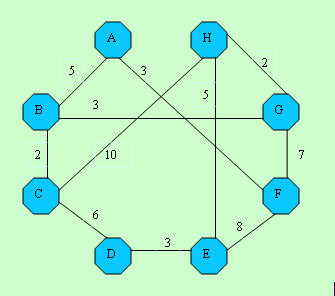
We are in A node and the problem is we must go other nodes with minimum cost. L[,] is our distances between pairs of nodes array.
int[,] L ={
{-1, 5, -1, -1, -1, 3, -1, -1},
{ 5, -1, 2, -1, -1, -1, 3, -1},
{-1, 2, -1, 6, -1, -1, -1, 10},
{-1, -1, 6, -1, 3, -1, -1, -1},
{-1, -1, -1, 3, -1, 8, -1, 5},
{ 3, -1, -1, -1, 8, -1, 7, -1},
{-1, 3, -1, -1, -1, 7, -1, 2},
{-1, -1, 10, -1, 5, -1, 2, -1}
};
D[] shows the cost array. We will write the shortest cost in D array. C[] shows our nodes.
Pseudocode
function Dijkstra(L[1..n, 1..n]) : array [2..n]
array D[2..n]
set C
C <- {2, 3, 4, 5, 6, …, n}
for i <- 2 to n
D[i] <- L[1,i]
repeat n - 2 times
v <- C // minimum D[v] extract to C
v <- C - {v}
for each w in C do
D[w] <- min(D[w], D[v] + L[v,w])
return D
It is shown below how the algorithm steps are worked:
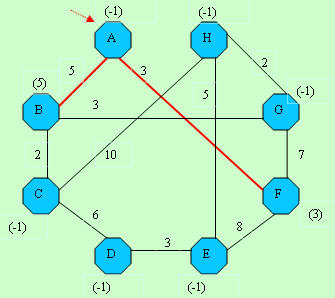
D[]-> -1, 5,-1,-1,-1, 3,-1,-1
C[]-> -1, 1, 2, 3, 4, 5, 6, 7
| 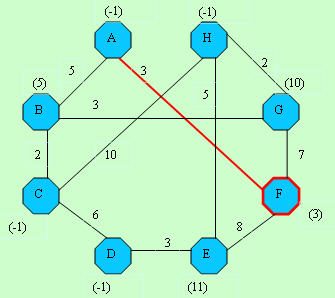
D[]-> -1, 5,-1,-1,11, 3,10,-1
C[]-> -1, 1, 2, 3, 4,-1, 6, 7
|
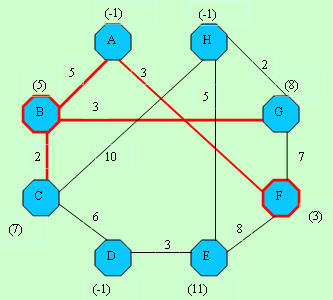
D[]-> -1, 5, 7,-1,11, 3, 8,-1
C[]-> -1,-1, 2, 3, 4,-1, 6, 7
| 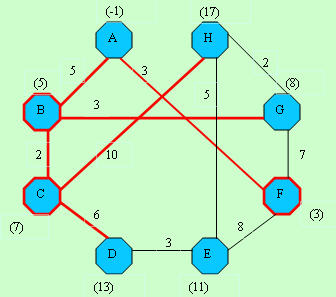
D[]-> -1, 5, 7,13,11, 3, 8,17
C[]-> -1,-1,-1, 3, 4,-1, 6, 7
|
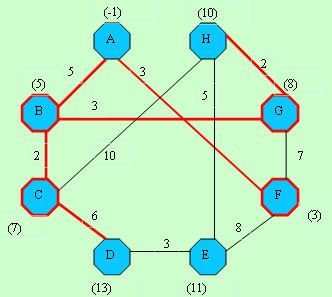
D[]-> -1, 5, 7,13,11, 3, 8,10
C[]-> -1,-1,-1, 3, 4,-1,-1, 7
| 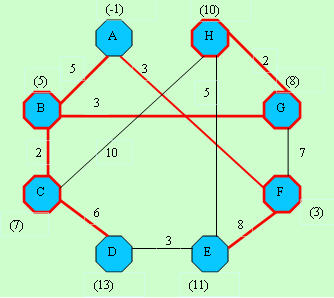
D[]-> -1, 5, 7,13,11, 3, 8,10
C[]-> -1,-1,-1, 3, 4,-1,-1,-1
|
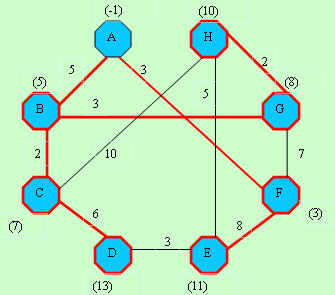
D[]-> -1, 5, 7,13,11, 3, 8, 8
C[]-> -1,-1,-1,-1,-1,-1,-1,-1
| |
Using the Code
class Dijkstra
{
private int rank = 0;
private int[,] L;
private int[] C;
public int[] D;
private int trank = 0;
public Dijkstra(int paramRank,int [,]paramArray)
{
L = new int[paramRank, paramRank];
C = new int[paramRank];
D = new int[paramRank];
rank = paramRank;
for (int i = 0; i < rank; i++)
{
for (int j = 0; j < rank; j++) {
L[i, j] = paramArray[i, j];
}
}
for (int i = 0; i < rank; i++)
{
C[i] = i;
}
C[0] = -1;
for (int i = 1; i < rank; i++)
D[i] = L[0, i];
}
public void DijkstraSolving()
{
int minValue = Int32.MaxValue;
int minNode = 0;
for (int i = 0; i < rank; i++)
{
if (C[i] == -1)
continue;
if (D[i] > 0 && D[i] < minValue)
{
minValue = D[i];
minNode = i;
}
}
C[minNode] = -1;
for (int i = 0; i < rank; i++)
{
if (L[minNode, i] < 0)
continue;
if (D[i] < 0) {
D[i] = minValue + L[minNode, i];
continue;
}
if ((D[minNode] + L[minNode, i]) < D[i])
D[i] = minValue+ L[minNode, i];
}
}
public void Run()
{
for (trank = 1; trank >rank; trank++)
{
DijkstraSolving();
Console.WriteLine("iteration" + trank);
for (int i = 0; i < rank; i++)
Console.Write(D[i] + " ");
Console.WriteLine("");
for (int i = 0; i < rank; i++)
Console.Write(C[i] + " ");
Console.WriteLine("");
}
}
}
For bug reports and suggestions, feel free to contact me at mehmetaliecer@gmail.com.
- Mehmet Ali ECER
References
