Introduction
Simulating the motion of an object within a real time environment with Gravity and Collision effects may not be a straightforward task in ordinary programming languages; doing such tasks require a good understanding of using timers and sometimes thread management, and this is why there are separate simulation tools for this and other similar tasks.
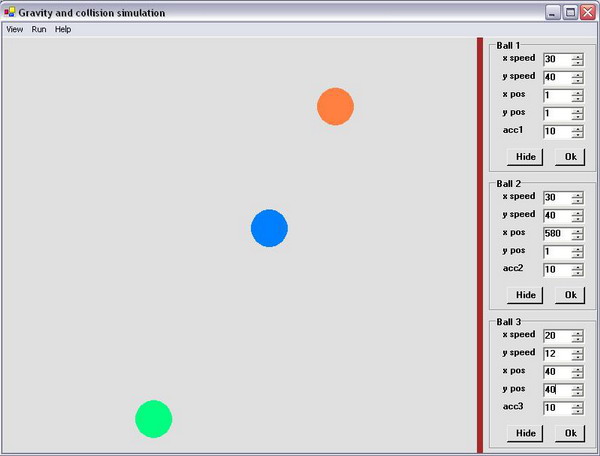
In this article, I will demonstrate to you how, using a timer and basic motion and collision equations, we could model the motion of three balls in a gravity enabled environment. You will see how these balls are going to collide each other and reflect from a wall, and even more, you can control their motion by updating some motion variables.
The motion of these balls is controlled and operated under the gravity and collision systems, using Newton's basic motion equations and collision equations. The positions of the three balls are updated every 20ms using a timer which will also take a snapshot of that motion.
Background
Before you see the code, I believe we should review the basic Gravity and Collision equations first.
Theoretical Analysis:
Gravity and motion equations:
The position equation:
X = Xi + Vx * tx
- Xi: Is the initial position of the object.
- Vx: Is a constant speed if we ignore the friction and air resistance, which I do include in this simulation. I consider the air as a constant resistance that must be taken care of periodically, so I divide the motion into separate periods and calculate the new position for each period.
- tx: Is the time.
Motion third equation:
Y = Y0 + Vy * ty – 0.5 * g * t^2
- g: The gravity acceleration.
The velocity equations:
Vy = Vy0 – g*t
- Vy: The final Y speed.
- Vy0: The initial Y speed.
- g: The gravity acceleration.
Vx = 0.99*Vx0
- Vx0: The old X speed.
- Vx: The new X speed after including air resistance.
- 0.99: Is a constant ratio representing air resistance.
Collision and preserved momentum:
Collision: an action between two or more bodies, each one affecting the others by a great power in a very short time, the bodies might not even touch!!!
+ Notes:
- The two bodies may be moving in opposite directions.
- The two bodies may be moving in the same direction.
- One is moving while the other is still.
- The power at the time of collision between two bodies can be represented as shown in the graph below:

- If two or more bodies collide, then the sum of their momentum before the collision is equal to the sum of their momentum after the collision.
Theory:
V1×m1 + V2×m2 = V1`×m1 + V2`×m2
Assuming same mass:
V1 + V2 = V1` + V2`

The code below will clarify these equations in their context.
Using the code
First of all, we should define the motion variables for each ball in our simulation.
double xspeed,yspeed,newyspeed,startingypos;
double newxpos,newypos,oldxpos,oldypos;
double newx,oldx,newy,oldy;
double acc,t;
const int ground = 500;
int xmouse,ymouse;
bool dragging=true,trace,collisiony;
int choice = 1;
int numberofballs = 1;
Ballinstance b1 = new Ballinstance();
Next, we will track the ball motion and check for a collision every 20 ms in our timer, and accordingly we will update the balls' positions.
private void timer_Elapsed(object sender, System.Timers.ElapsedEventArgs e)
{
b1.play(ref xspeed,ref yspeed,
ref newyspeed,ref startingypos,
ref newxpos,ref newypos,ref oldxpos,ref oldypos,
ref newx,ref oldx,ref newy,ref oldy,
ref acc,ref t,
ref xmouse,ref ymouse,
ref dragging,ref trace,ref collisiony);
ball.Left = (int)newxpos;
ball.Top = (int)(ground - newypos);
Collision();
}
Below is the Ballinstance class, and the play function where most of the work is done. As you will see, this function will be visited every 20 ms, the timer period, and then will check for the calling ball status, which can be as follows:
- Dragging state:
If the ball calling the play function was in the drag mode, then the ball position will be updated according to the mouse pointer position, and the ball's initial speed will be calculated by measuring the change of the ball position between two successive calls to the play function; within 20 ms.
- Motion state:
If the ball calling the play function wasn't in the drag mode, then the ball position will be updated according to Newton's and projectile motion equations and the Collision preserved momentum equation.
public class Ballinstance
{
int xpos,ypos;
const int ground = 500;
public void play(ref double xspeed,
ref double yspeed,
ref double newyspeed,
ref double startingypos,
ref double newxpos,
ref double newypos,
ref double oldxpos,
ref double oldypos,
ref double newx,
ref double oldx,
ref double newy,
ref double oldy,
ref double acc,
ref double t,
ref int xmouse,
ref int ymouse,
ref bool dragging,
ref bool trace,
ref bool collisiony)
{
xpos = (int)newxpos;
ypos = (int)newypos;
if (dragging)
{
xpos = xmouse;
ypos = ymouse;
startingypos = ground - ypos;
newx = xpos;
newy = ground - ypos;
xspeed = (newx-oldx)/1;
yspeed = (newy-oldy)/1;
oldx = newx;
oldy = newy;
t=0;
}
else
{
oldxpos = xpos;
if(xpos < 580 && 0 < xpos)
{
newxpos = oldxpos + xspeed;
}
else
{
xspeed *= -0.9;
newxpos = oldxpos + xspeed;
}
if(0 < newypos || collisiony)
{
newyspeed = yspeed - (acc*t);
newypos = startingypos + ((yspeed*t)- 0.5*acc*(t*t));
collisiony = false;
}
else
{
startingypos = -1;
t = 0;
yspeed = newyspeed * -0.75;
newypos = startingypos + ((yspeed*t)- 0.5*acc*(t*t));
collisiony = true;
}
xspeed *= 0.99;
#region explination of xspeed condition
#endregion
if(xspeed > -0.5 && xspeed < 0)
xspeed = 0;
xpos = (int)newxpos;
ypos = (int)(ground - newypos);
t += 0.3;
}
}
}
Conclusion
The project is not completed yet. I was thinking of creating some obstacles to see how the balls will collide them, seems funny :). You also can improve the way it looks and make it more usable if you write a routine to drag and drop the ball by grapping it, which I can't find out how to do in C#!!
I'd like to thank Anas Trad and Du3a2 Al-ansari, my friends, for their contributions to help finish this simulation.
History
- Gravity simulation version 1.0.
