There are other languages like F# that have better support for functional programming and you can use it with C# code. However, if you do not want to learn a new language, in this article, you can find what C# provides you in the functional programming area.
Table of Contents
- Introduction
- Functions as First-Class Values
- Function Types
- Function Values
- Function/Delegate Arithmetic
- C# Functional Programming
- Using Linq
- Higher-Order Functions
- Asynchronous Functions
- Tuples
- Closures
- Recursion
- Partial Functions
- Curry Functions
- Conclusion
- History
Introduction
Functional programming is a programming paradigm in C# that is frequently combined with object oriented programming. C# enables you to use imperative programming using object-oriented concepts, but you can also use declarative programming. In declarative programming, you are using a more descriptive way to define what you want to do and not how you want to do some action. As an example, imagine that you want to find the top 10 books with price less than 20 ordered by title. In functional programming, you will define something like:
books.Where(price<20).OrderBy(title).Take(10);
Here, you just specify that you want to select books where the price is less than 20, order them by title, and take the first ten. As you can see, you do not specify how this should be done - only what you want to do.
Now you will say "OK, but this is just simple C# LINQ - why are we calling it functional programming"? LINQ is just one implementation library that enables you to use functional programming concepts. However, functional programming is much more. In this article, you might find some interesting samples of usage.
Note that there are other languages that have better support for functional programming. An example might be the F# language that has better support for functional programming concepts and you can use it with C# code. However, if you do not want to learn a new language, here you can find what C# provides you in the functional programming area.
Functions as First-Class Values
The base concept in functional programming is functions. In functional programming, we need to create functions as any other objects, manipulate them, pass them to other functions, etc. Therefore, we need more freedom because functions are not just parts of classes - they should be independent objects. In C#, you can use a function object as any other object type. In the following sections, you can see how we can define function types, assign values to function objects (references), and create complex functions.
Function Types
Function objects must have some type. In C#, we can define either generic functions or strongly typed delegates. Delegates might be recognized as a definition of function prototypes where the method signature is defined. "Instance objects" of delegate types are pointers to functions (static methods, class methods) that have a prototype that matches the delegate definition. An example of a delegate definition is shown in the following code:
delegate double MyFunction(double x);
This delegate defines a prototype of a function that has a double argument and returns the result as a double value. Note that only types are important, actual names of methods and their arguments are arbitrary. This delegate type matches a lot of trigonometric functions, logarithm, exponential, polynomial, and other functions. As an example, you can define a function variable that references some math function, executes it via a function variable, and puts the result in some other variable. An example is shown in the following listing:
MyFunction f = Math.Sin;
double y = f(4);
f = Math.Exp;
y = f(4);
Instead of strongly typed delegates, you can use generic function types Func<T1, T2, T3, ...,Tn, Tresult> where T1, T2, T3, ...,Tn are types of the arguments (used if the function has some arguments) and Tresult is the return type. An example equivalent to the previous code is shown in the following listing:
Func<double, double> f = Math.Sin;
double y = f(4);
f = Math.Exp;
y = f(4);
You can either define your named delegates or use generic types. Besides Func, you have two similar generic types:
- Predicate<T1, T2, T3, ...,Tn> that represents a function that returns a
true/false value - equivalent to Func<T1, T2, T3, ...,Tn, bool> - Action<T1, T2, T3, ...,Tn> that represents a procedure that does not returns any value - equivalent to Func<T1, T2, T3, ...,Tn, void>
Predicate is a function that takes some arguments and returns either a true or false value. In the following example, a predicate function that accepts a string parameter is shown. The value of this function is set to String.IsNullOrEmpty. This function accepts a string argument and returns information whether or not this string is null or empty - therefore, it matches the Predicate<string> type.
Predicate<string> isEmptyString = String.IsNullOrEmpty;
if (isEmptyString("Test"))
{
throw new Exception("'Test' cannot be empty");
}
Instead of Predicate<string>, you could use Func<string, bool>.
Actions are a kind of procedures that can be executed. They accept some arguments but return nothing. In the following example, one action that accepts string argument is shown and it points to the standard Console.WriteLine method.
Action<string> println = Console.WriteLine;
println("Test");
When an action reference is called with the parameter, the call is forwarded to the Console.WriteLine method. When you use Action types, you just need to define the list of input parameters because there is no result. In this example, Action<string> is equivalent to Func<string, void>.
Function Values
Once you define function objects, you can assign them other existing functions as shown in the previous listings or other function variables. Also, you can pass them to other functions as standard variables. If you want to assign a value to a function, you have the following possibilities:
- Point the function object to reference some existing method by name.
- Create an anonymous function using the lambda expression or delegate and assign it to the function object.
- Create a function expression where you can add or subtract a function and assign that kind of multicast delegate to the function object (described in the next section).
Some examples of assigning values to functions are shown in the following listing:
Func<double, double> f1 = Math.Sin;
Func<double, double> f2 = Math.Exp;
double y = f1(4) + f2(5);
f2 = f1;
y = f2(9);
In this case, methods are referred as ClassName.MethodName. Instead of existing functions, you can dynamically create functions and assign them to variables. In this case, you can use either anonymous delegates or lambda expressions. An example is shown in the following listing:
Func<double, double> f = delegate(double x) { return 3*x+1; }
double y = f(4);
f = x => 3*x+1;
y = f(5);
In this code, we have assigned a delegate that accepts a double argument x and returns a double value 3*x+1. As this dynamically created function matches Func<double, double>, it can be assigned to the function variable. In the third line, an equivalent lambda expression is assigned. As you can see, the lambda expression is identical to the function: it is just a function representation in the format parameters => return-expression. In the following table, some lambda expressions and equivalent delegates are shown:
| Lambda expression | Delegate |
| () => 3
| delegate(){ return 3; } |
() => DateTime.Now | delegate(){ return DateTime.Now; }; |
(x) => x+1 | delegate(int x){ return x+1; } |
x => Math.Log(x+1)-1 | delegate(int x){ return Math.Log(x+1)-1; } |
(x, y) => x+y | delegate(int x, int y){ return x+y;} |
(x, y) => x+y | delegate(string x, string y){ return x+y;} |
Lambda expression must have part for definition of argument names - if lambda expression does not have parameters, empty brackets () should be placed. If there is only one parameter in the list, brackets are not needed. After => sign, you need to put an expression that will be returned.
As you can see, lambda expressions are equivalent to regular functions (delegates), but they are more suitable when you are creating short functions. Also, one useful advantage is that you do not have to explicitly define parameter types. In the example above, lambda expression (x, y) => x+y is defined that can be used both for adding numbers but also for concatenating strings. If you use delegates. you will need to explicitly define argument types, and you cannot use one delegate for other types.
The ability to build your own functions might be useful when you need to create your own new functions. As an example, you can create some math functions that are not part of Math class but you need to use them. Some of these functions are:
- asinh(x) = log(x + sqrt(x2 + 1))
- acosh(x) = log(x + sqrt(x2 - 1))
- atanh(x) = (log(1+x) - log(1-x))/2
You can easily create these functions and set them to the functional variables as it is shown in the following listing:
Func<double, double> asinh = delegate(double x) { return Math.Log( x + Math.Sqrt(x*x+1) ) ;
Func<double, double> acosh = x => Math.Log( x + Math.Sqrt(x*x-1) ) ;
Func<double, double> atanh = x => 0.5*( Math.Log( 1 + x ) - Math.Log( 1 -x ) ) ;
You can create these functions either via delegates or lambda expressions as they are equivalent.
Function Arithmetic
You can also add or subtract functions (delegates) in expressions. If you add two function values, when the resulting function variable is called, both functions will be executed. This is the so called multicast delegate. You can also remove some functions from the multicast delegate. In the following example, I have added two functions that match the Action<string> type:
static void Hello(string s)
{
System.Console.WriteLine(" Hello, {0}!", s);
}
static void Goodbye(string s)
{
System.Console.WriteLine(" Goodbye, {0}!", s);
}
These methods accept a string parameter and return nothing. In the following code, how you can apply delegate arithmetic in order to manipulate multicast delegates is shown.
Action<string> action = Console.WriteLine;
Action<string> hello = Hello;
Action<string> goodbye = Goodbye;
action += Hello;
action += (x) => { Console.WriteLine(" Greating {0} from lambda expression", x); };
action("First");
action -= hello;
action("Second");
action = Console.WriteLine + goodbye
+ delegate(string x){
Console.WriteLine(" Greating {0} from delegate", x);
};
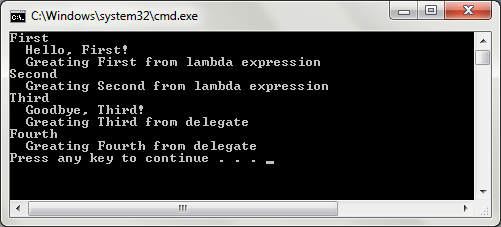
action("Third");
(action - Goodbye)("Fourth");
First, we have created three delegates pointing to the functions, WriteLine, Hello and Goodbye. Then, we have added a function Hello and a new lambda expression to the first delegate. Operator += is used for attaching new functions that will be called by the multicast delegate. In the end, it will create a multicast delegate that will call all three functions once it is called.
Then, the function Hello is removed from the delegate action. Note that the function Hello is added directly via name, but it is removed via the delegate hello that points to it. When the action is called a second time, only two functions will be called.
In the third group, the WriteLine delegate to the Goodbye method and a new anonymous delegate are added. This "sum" is assigned to the delegate action so the previous combination is lost. When the action ("Third") is called, these three functions are executed.
In the end, you can see how you can create an expression and execute it. In the last statement, the result of the expression action - goodbye is a function mix in the action without the Goodbye function. The result of the expression is not assigned to any delegate variable - it is just executed.
If you put this code in some console application, the result would be similar to the following screenshot:
Also, you can always get the information about the current function set in the multicast delegate. The following code gets the invocation list of multicast delegate action and for each delegate in the invocation list outputs the name of the method:
action.GetInvocationList().ToList().ForEach(del => Console.WriteLine(del.Method.Name));
Beside the name, you can get other parameters of the function such as return type, arguments, and you can even explicitly call some delegates in the invocation list.
C# Functional Programming
Now we can start with functional programming examples. The fact that functions can be passed as arguments enables us to create very generic constructions. As an example, imagine that you want to create a generic function that determines the number of objects in some array that satisfies some condition. The following example shows how this function can be implemented:
public static int Count<T>(T[] arr, Predicate<T> condition)
{
int counter = 0;
for (int i = 0; i < arr.Length; i++)
if (condition(arr[i]))
counter++;
return counter;
}
In this function, we are counting the elements in the array that satisfies the condition. Code that determines whether the condition is satisfied is not hard-coded in the function and it is passed as an argument (predicate). This function can be used in various cases such as counting the number of books where the title is longer that 10 characters, or where the price is less than 20, or counting the negative numbers in the array. Some examples are shown below:
Predicate<string> longWords = delegate(string word) { return word.Length > 10; };
int numberOfBooksWithLongNames = Count(words, longWords);
int numberOfCheapbooks = Count(books, delegate(Book b) { return b.Price< 20; });
int numberOfNegativeNumbers = Count(numbers, x => x < 0);
int numberOfEmptyBookTitles = Count(words, String.IsNullOrEmpty);
As you can see, the same function is used in different areas - you just need to define a different condition (predicate) that should be applied in the function. A predicate can be a delegate, lambda expression, or existing static function.
You can use functional programming to replace some standard C# constructions. One typical example is using block shown in the following listing:
using (obj)
{
obj.DoAction();
}
Using block is applied on the disposable objects. In the using block, you can work with the object, call some of the methods, etc. When using block ends, object will be disposed. Instead of the using block, you can create your own function that will warp the action that will be applied on the object.
public static void Use<T>(this T obj, Action<T> action) where T : IDisposable
{
using (obj)
{
action(obj);
}
}
Here is created one extension method that accepts action that should be executed and wrap call in the using block. The following code shows an example of usage:
obj.Use( x=> x.DoAction(); );
You can convert any structure such as if, while, foreach to function. In the following example, you can see how you can output names from the list of strings using the ForEach extension method that is just equivalent to the foreach loop:
var names = new List<string>();
names.ForEach(n => Console.WriteLine(n));
Method of the List<T> class ForEach<T>(Action<T> action) works the same way as a standard for each loop, but this way, you have more compact syntax. In the following examples, you will see some common usages of functional programming.
Using LINQ
The function that you saw in the previous listing is very generic and useful, but in most cases, you do not even have to create it. C# comes with a LINQ extension where you can find many useful generic functions. As an example, you can use the LINQ Count method instead of the one defined in the previous example to do the same thing. The same examples written with the LINQ Count function are:
Predicate<string> longWords = delegate(string word) { return word.Length > 10; };
int numberOfBooksWithLongNames = words.Count(longWords);
int numberOfCheapbooks = books.Count( delegate(Book b) { return b.Price< 20; });
int numberOfNegativeNumbers = numbers.Count(x => x < 0);
This function is directly built-in so you can use it. LINQ has many other useful functions such as Average, Any and Min that can be used the same way - just pass the predicate that should be used to check whether or not some objects in the array should be included. Some examples of other LINQ functions are shown in the following listing:
int averageDigits = number.Average( digit => digit>=0 && digit < 10);
int isAnyCheaperThan200 = books.Any( b => b.Price< 200 );
int maxNegativeNumber = numbers.Max(x => x < 0);
In the LINQ library, you have many functions that you can use out of box for functional programming. As an example, you have a set of function that accepts predicate and process source collection - some of them are:
- <source>.Where( <predicate> ) - finds all entities in the source that satisfy predicate
- <source>.First( <predicate> ) - finds first entity in the source that satisfies predicate
- <source>.Count( <predicate> ) - finds number of entities in the source that satisfy predicate
- <source>.TakeWhile( <predicate> ) - takes a sequence of elements in the source that satisfies some predicate
- <source>.SkipWhile( <predicate> ) - skip entities in the source that satisfies predicate
- <source>.Any( <predicate> ) - check whether any object in the source satisfies the condition in predicate
- <source>.All( <predicate> ) - check whether all objects in the source satisfy the condition in predicate
You can see more details about these methods in Using LINQ Queries article. LINQ has functions that work with regular functions that return some values. As an example, if you pass criterion function that returns string or int, you can order elements of collection using the following functions:
<source>.OrderBy(<criterion>).ThenBy(<criterion>)
Criterion is any function that for each element in the source collection returns some value that can be used for ordering.
I will not show too many details of LINQ here, but if you are interested in this, you can see the Using LINQ Queries article. However, I will just show some examples of usage that some are not aware of.
Imagine that you need to find the number of nulls or empty strings in an array of strings. Code for this looks like:
string[] words = new string[] { "C#", ".NET", null, "MVC", "", "Visual Studio" };
int num = words.Count( String.IsNullOrEmpty );
As you can see, you do not always need to pass a lambda expression to the LINQ function. LINQ functions expect some predicate so you can pass a lambda expression (in 90% cases, you will do it this way), but you can also directly pass a function that should be evaluated.
In practice, you will use LINQ for 90% of any functionalities you need to implement, and you will create custom functions only for functionalities that are not already provided.
Higher Order Functions
Treating functions as regular objects enables us to use them as arguments and results of other functions. Functions that handle other functions are called higher order functions. The Count function in the example above is a higher-order function because it accepts a predicate function and applies it to each element when it checks the condition. Higher-order functions are common when using the LINQ library. As an example, if you want to convert a sequence to a new sequence using some function, you will use something like the Select LINQ function:
var squares = numbers.Select( num => num*num );
In the example above, you can see a LINQ function Select that maps each number in the collection of numbers to its square value. This Select function is nothing special, it can be easily implemented as the following higher-order function:
public static IEnumerable<T2> MySelect<T1, T2>(this IEnumerable<T1> data, Func<T1, T2> f)
{
List<T2> retVal= new List<T2>();
foreach (T1 x in data) retVal.Add(f(x));
return retVal;
}
In this example, the function iterates through the list, applies the function f to each element, puts the result in the new list, and returns the collection. By changing function f, you can create various transformations of the original sequence using the same generic higher order function. You can see more examples of this function in Akram's comment below.
Example - Function Composition
Here, you can see how higher-order functions can be used to implement composition of two functions. Let's imagine that we have function f (of type Func<X,Y>) that converts elements of type X to the elements of type Y. Also, we would need another function g (of type Func<Y,Z>) that converts elements of type Y to the elements of type Z. These functions and element sets are shown in the following figure:

Now, we would like to create a single function, fog(x), that converts elements of type X directly to the elements of type Z (type of the function is Func<X,Z>). This function will work following way - first, it will apply function f to some element of type X in order to calculate element from the set Y, and then it will apply function g on the results. This formula is shown below:
This function that represents composition of functions f and g has type Func<X,Z> and directly maps the elements of type X to the elements of type Z. This is shown in the following figure:

Now, we can create higher-order function that implements this composition. This function will accept two functions with generic types, Func<X,Y> and Func<Y,Z> that represent functions that will be composed, and returns one function of type Func<X,Z> that represents resulting composition. The code of the higher-order function that creates composition of two functions is shown in the following listing:
static Func<X, Z> Compose<X, Y, Z>(Func<X, Y> f, Func<Y, Z> g)
{
return (x) => g(f(x));
}
As described above, this higher-order function takes two functions, f and g and creates a new function that accepts parameter x and calculates g(f(x)). According to the definition above, this is composition of functions.
If you want to use this function to create a function that calculates exp(sin(x)), you will use code that looks like the following one:
Func<double, double> sin = Math.Sin;
Func<double, double> exp = Math.Exp;
Func<double, double> exp_sin = Compose(sin, exp);
double y = exp_sin(3);
In this case, X, Y and Z are the same types - double.
As you can see, the result of the Compose function is not a value - it is a new function that can be executed. You can use a similar approach to generate your own functions.
Asynchronous Functions
One of the important features of functions is that they can be called asynchronously, i.e., you can start a function, continue with the work, and then wait until the function finishes when you need results. Each function object in C# has the following methods:
BeginInvoke that starts function execution but does not wait for the function to finishIsCompleted that checks whether the execution is finishedEndInvoke that blocks execution of the current thread until the function is completed
An example of asynchronous execution of the function is shown in the following listing:
Func<int, int, int> f = Klass.SlowFunction;
IAsyncResult async = f.BeginInvoke(5, 3, null, null);
if(async.IsCompleted) {
int result = f.EndInvoke(async);
}
int sum = f.EndInvoke(async);
In this example, a reference to some slow function that calculates the sum of two numbers is assigned to the function variable f. You can separately begin invocation and pass arguments, check if the calculation was finished, and explicitly demand result. An example of that kind of function is shown in the following listing:
public class Klass{
public static int SlowFunction(int x, int y){
Thread.Sleep(10000);
return x+y;
}
}
This is just a simulation, but you can use this approach in functions that send emails, execute long SQL queries, etc.
Asynchronous Functions With Callbacks
In the previous example, you saw that arguments are passed to the function, but there are also two additional parameters set to null. These arguments are:
- Callback function that will be called when the function finishes
- Some object that will be passed to the callback function
This way, you do not need to explicitly check if the function was executed - just pass the callback function that will be called when the function finishes execution. An example of the call with callback is shown in the following code:
Func<int, int, int> f = Klass.SlowFunction;
f.BeginInvoke(5, 3, async =>
{
string arguments = (string)async.AsyncState;
var ar = (AsyncResult)async;
var fn = (Func<int, int, int>)ar.AsyncDelegate;
int result = fn.EndInvoke(async);
Console.WriteLine("f({0}) = {1}", arguments, result);
},
"5,3"
);
The callback function (or lambda expression in this example) takes a parameter async that has information about the asynchronous call. You can use the AsyncState property to determine the fourth argument of the BeginInvoke call (in this case are passed arguments as string "5,3"). If you cast the parameter of the lambda expression to AsyncResults, you can find the original function and call its EndInvoke method. As a result, you can print it on the console window.
As you can see, there is no need to explicitly check in the main code if the function has finished - just let it know what should be done when it is completed.
Tuples
Tuples are a useful way to dynamically represent a data structure in the form (1, "name", 2, true, 7). You can create tuples by passing a set of fields that belong to the tuple to the Tuple.Create method. An example of a function that uses tuples is shown below:
Random rnd = new Random();
Tuple<double, double> CreateRandomPoint() {
var x = rnd.NextDouble() * 10;
var y = rnd.NextDouble() * 10;
return Tuple.Create(x, y);
}
This function creates a random 2D point within area 10x10. Instead of the tuple, you could explicitly define a class Point and pass it in the definition, but this way we have a more generic form.
Tuples can be used when you want to define generic functions that use structured data. If you want to create a predicate that determines whether a 2D point is placed within a circle with radius 1, you will use something like the following code:
Predicate<Tuple<double, double>> isInCircle;
isInCircle = t => ( t.Item1*t.Item1+t.Item2*t.Item2 < 1 );
Here, we have a predicate that takes a tuple with two double items and determines whether the coordinates are in the circle. You can access any field in the tuple using properties Item1, Item2, etc. Now let us see how we can use this function and predicate to find all points that are placed within the circle with radius 1.
for(int i=0; i<100; i++){
var point = CreateRandomPoint();
if(isInCircle(t))
Console.WriteLine("Point {0} in placed within the circle with radius 1", point);
}
Here, we have a loop where we generate 100 random points and for each of them, we check whether the isInCircle function is satisfied.
You can use tuples when want to create data structure without creating a predefined class. Tuples can be used in the same code where you are using dynamic or anonymous objects, but one advantage of tuples is that you can use them as parameters or return values.
Here is one more complex example - imagine that you have represented information about company as tuples of type Tuple<int, string, bool, int> where the first item is ID, second is the name of the company, third is a flag that marks the tuple as branch, and the last item is the ID of the head office. This is very common if you create some kind of query like SELECT id, name, isOffice, parentOfficeID and where you put each column in a separate dimension of the tuple. Now, we will create a function that takes a tuple and creates a new branch office tuple:
Tuple<int, string, bool, int?> CreateBranchOffice(Tuple<int, string, bool, int?> company){
var branch = Tuple.Create(1, company.Item2, company.Item3, null);
Console.WriteLine(company);
branch = Tuple.Create(10*company.Item1+1, company.Item2 +
" Office", true, company.Item1);
Console.WriteLine(t);
var office = new { ID = branch.Item1,
Name = branch.Item2,
IsOffice = branch.Item3,
ParentID = company.Item4 };
return branch;
}
In this example, the function accepts company and creates a branch office. Both company and branch offices are represented as tuples with four items. You can create a new tuple using the Tuple.Create method, and access the elements of the tuple using the Item properties.
Also, in this code, an anonymous object office with properties ID, Name, IsOffice, and ParentID is created which is equivalent to tuple (this object is just created but not used anywhere). In this statement, you can see how easy it is to convert tuples to actual objects. Also, you can see one advantage of tuples - if you would like to return office as a return value, you would have a problem defining the return type of the function CreateBranchOffice. The office object is an anonymous object, its class is not known by name outside of the function body, therefore you cannot define the return type of the function. If you want to return some dynamic structure instead of tuple, you would need to define a separate class instead of an anonymous class, or you will need to set the return type as dynamic but in that case, you will lose information about the structure of the returned object.
Closures
When we are talking about the functions, we must talk about scope of variables. In the standard functions, we have the following types of variables:
- Arguments that are passed to the function
- Local variables that are defined and used inside the function body. They are destroyed immediately when function finishes.
- Global variables that are defined out of the function and referenced in the function body. These variables live even when the function ends.
When we create a delegate or lambda expression, we use arguments and local variables, and we can reference variables outside the delegate. Example is shown in the following listing:
int val = 0;
Func<int, int> add = delegate(int delta) { val+=delta; return val; };
val = 10;
var x = add(5);
var y = add(7);
Here, we have created one delegate that adds value of the parameter to the variable val that is defined outside the delegate. Also, it returns a value as result. We can modify the variable val both in the main code and indirectly via delegate call.
Now what will happens if variable val is a local variable in the higher-order function that returns this delegate? Example of that kind of function is shown in the following listing:
static Func<int, int> ReturnClosureFunction()
{
int val = 0;
Func<int, int> add = delegate(int delta) { val += delta; return val; };
val = 10;
return add;
}
And with the calling code:
Func<int, int> add = ReturnClosureFunction();
var x = add(5);
var y = add(7);
This might be a problem because local variable val dies when ReturnClosureFunction is finished, but the delegate is returned and still lives in the calling code. Would the delegate code break because it references variable val that does not exist outside the function ReturnClosureFunction? Answer is - no. If delegate references the outside variable, it will be bound to the delegate as long as it lives in any scope. This means that in the calling code above will set the values 15 in the variable x, and 22 in the variable y. If a delegate references some variable outside his scope, this variable will behave as a property of the function object (delegate) - it will be part of the function whenever the function is called.
We will see how closures are used in the two following examples.
Example 1 - Shared Data
This interesting feature might be used to implement sharing data between the functions. Using the closures to share variables, you can implement various data structures such as lists, stack, queues, etc, and just expose delegates that modify shared data. As an example, let us examine the following code:
int val = 0;
Action increment = () => val++;
Action decrement = delegate() { val--; };
Action print = () => Console.WriteLine("val = " + val);
increment();
print();
increment();
print();
increment();
print();
decrement();
print();
Here, we have one variable that is updated by the lambda expression increment and delegate decrement. Also, it is used by the delegate print. Each time you use any of the functions, they will read/update the same shared variable. This will work even if the shared variable is out of scope of usage. As an example, we can create a function where this local variable is defined, and this function will return three functions:
static Tuple<Action, Action, Action> CreateBoundFunctions()
{
int val = 0;
Action increment = () => val++;
Action decrement = delegate() { val--; };
Action print = () => Console.WriteLine("val = " + val);
return Tuple.Create<Action, Action, Action>(increment, decrement, print);
}
In this example, we are returning a tuple with three actions as a return result. The following code shows how we can use these three functions outside the code where they are created:
var tuple = CreateBoundFunctions();
Action increment = tuple.Item1;
Action decrement = tuple.Item2;
Action print = tuple.Item3;
increment();
print();
increment();
print();
increment();
print();
decrement();
print();
This code is identical to the previous code where all three functions are created in the same scope. Each time we call some of the bounded functions, they will modify the shared variable that is not in the scope anymore.
Example 2 - Caching
Now we will see another way how to use closures to implement caching. Caching can be implemented if we create a function that accepts function that should be cached, and return a new function that will cache results in some period. Example is shown in the following listing:
public static Func<T> Cache<T>(this Func<T> func, int cacheInterval)
{
var cachedValue = func();
var timeCached = DateTime.Now;
Func<T> cachedFunc = () => {
if ((DateTime.Now - timeCached).Seconds >= cacheInterval)
{
timeCached = DateTime.Now;
cachedValue = func();
}
return cachedValue;
};
return cachedFunc;
}
Here, we have extended functions that return some type T (Func<T> func). This extension method accepts period for caching value of function and returns a new function. First, we have executed function in order to determine a value that will be cached and record time when it is cached. Then we have created a new function cachedFunc with the same type Func<T>. This function determines whether the difference between the current time and time when the value is cached is greater or equal of cache interval. If so, new cache time will be set to the current time and cached value is updated. As a result, this function will return cached value.
Variables cacheInterval, cachedValue and timeCached are bound to the cached function and behaves as a part of the function. This enables us to memoize last value and determine how long it should be cached.
In the following example, we can see how this extension can be used to cache value of the function that returns the current time:
Func<DateTime> now = () => DateTime.Now;
Func<DateTime> nowCached = now.Cache(4);
Console.WriteLine("\tCurrent time\tCached time");
for (int i = 0; i < 20; i++)
{
Console.WriteLine("{0}.\t{1:T}\t{2:T}", i+1, now(), nowCached());
Thread.Sleep(1000);
}
We have created a function that accepts no arguments and returns a current date (the first lambda expression). Then we have applied Cache extension function on this function in order to create cached version. This cached version will return the same value in the 4 seconds interval.
In order to demonstrate caching in the for loop are outputted values of the original and the cached version. Result is shown in the following output window:

As you can see, the cached version of function returns the same time value each four seconds as it is defined in the caching interval.
Recursion
Recursion is the ability that function can call itself. One of the most commonly used examples of recursion is calculation of factorial of an integer number. Factorial of n (Fact(n) = n!) is a product of all numbers less or equal to n, i.e., n! = n*(n-1)*(n-2)*(n-3)*...*3*2*1. There is one interesting thing in the definition of factorial n! = n * (n-1)! and this feature is used to define recursion.
If n is 1, then we do not need to calculate factorial - it is 1. If n is greater than 1, we can calculate factorial of n-1 and multiply it with n. An example of that kind of a recursive function is shown in the following listing:
static int Factorial(int n)
{
return n < 1 ? 1 : n * Factorial(n - 1);
}
This is easy in the statically named function but you cannot do this directly in delegates/lambda expressions because they cannot reference themselves by name. However, there is a trick to how you can implement recursion:
static Func<int, int> Factorial()
{
Func<int, int> factorial = null;
factorial = n => n < 1 ? 1 : n * factorial(n - 1);
return factorial;
}
In this higher-order function (it returns a function object) factorial is defined as a local variable. Then, factorial is assigned to the lambda expression that uses the logic above (if argument is 1 or less, return 1, otherwise call factorial with argument n-1). This way, we have declared a function before its definition and in the definition, we have used a reference to recursively call it. In the following example, how you can use this recursive function is shown:
var f = Factorial();
for(int i=0; i<10; i++)
Console.WriteLine("{0}! = {1}", i, f(i));
If you can implement factorial as a higher-order function, then it means that you can format it as an anonymous function. In the following example, you can see how you can define a delegate that determines the factorial of a number. This delegate is used in LINQ in order to find all numbers with factorial less than 7.
var numbers = new[] { 5,1,3,7,2,6,4};
Func<int, int> factorial = delegate(int num) {
Func<int, int> locFactorial = null;
locFactorial = n => n == 1 ? 1 : n * locFactorial(n - 1);
return locFactorial(num);
};
var smallnums = numbers.Where(n => factorial(n) < 7);
Also, you can convert it to a lambda expression and pass it directly to the LINQ function as shown in the following example:
var numbers = new[] { 5,1,3,7,2,6,4};
var smallnums = numbers.Where(num => {
Func<int, int> factorial = null;
factorial = n => n == 1 ? 1 : n * factorial(n - 1);
return factorial(num) < 7;
});
Unfortunately, this lambda expression is not compact as you might expect because we need to define the local factorial function. As you can see, it is possible to implement recursion even with the anonymous functions/lambda expressions.
Partial Functions
Partial functions are functions that reduce the number of function arguments by using default values. If you have a function with N parameters, you can create a wrapper function with N-1 parameters that calls the original function with a fixed (default) argument.
Imagine that you have a function Func<double, double, double> that has two double arguments and returns one double result. You might want to create a new single argument function that has the default value for the first argument. In that case, you will create a partial higher-order function that accepts the default value for the first argument and creates a single argument function that always passes the same first value to the original function and the only argument just passes the argument to the function and sets the default value:
public static Func<T2, TR> Partial1<T1, T2, TR>(this Func<T1, T2, TR> func, T1 first)
{
return b => func(first, b);
}
Math.Pow(double, double) is an example of a function that can be extended with this partial function. Using this function, we can set the default first argument and derive functions such as 2x, ex (Math.Exp), 5x, 10x, etc. An example is shown below:
double x;
Func<double, double, double> pow = Math.Pow;
Func<double, double> exp = pow.Partial1( Math.E );
Func<double, double> step = pow.Partial1( 2 );
if (exp(4) == Math.Exp(4))
x = step(5);
Instead of the first argument, we can set the second one as default. In that case, partial function would look like the following one:
public static Func<T1, TR> Partial2<T1, T2, TR>(this Func<T1, T2, TR> func, T2 second)
{
return a => func(a, second);
}
Using this function, we can derive from the Math.Pow functions such as square x2, square root √ x , cube x3, etc. Code that derives these functions from Math.Pow is shown in the following listing:
double x;
Func<double, double, double> pow = Math.Pow;
Func<double, double> square = pow.Partial2( 2 );
Func<double, double> squareroot = pow.Partial2( 0.5 );
Func<double, double> cube = pow.Partial2( 3 );
x = square(5);
x = sqrt(9);
x = cube(3);
In the following example, how you can use this feature will be shown.
Example - Reducing Spatial Dimensions
I will explain partial functions (and currying later) with a mathematical example - determining the distance of a point in a three dimensional coordinate system. A point in a 3D coordinate system is shown in the following figure. As you can see, each point has three coordinates - one for each axis.

Imagine that you need to determine the distance from the point to the center of the coordinate system (0,0,0). This function would look like:
static double Distance(double x, double y, double z)
{
return Math.Sqrt(x * x + y * y + z * z);
}
This function determines the standard Euclid distance in three dimensional space. You can use this function as any other function:
Func<double, double, double, double> distance3D = Distance;
var d1 = distance3D(3, 6, -1);
var d2 = distance3D(3, 6, 0);
var d3 = distance3D(3, 4, 0);
var d4 = distance3D(3, 3, 0);
Imagine that you are always working with points on the ground level - these are 2D points with the last coordinate (altitude) always at z=0. On the previous figure, a Pxy point (projection of point P in the xy plane) is shown where the z coordinate is 0. If you are working with two dimensional points in the XY plane and you want to determine the distances of these points from the center, you can use the Distance function, but you will need to repeat the last argument z=0 in each call, or you will need to rewrite the original function to use only two dimensions. However, you can create a higher-order function that accepts the original 3D function and returns a 2D function where the default value for z is always set. This function is shown in the following example:
static Func<T1, T2, TResult> SetDefaultArgument<T1, T2, T3,
TResult>(this Func<T1, T2, T3, TResult> function, T3 defaultZ)
{
return (x, y) => function(x, y, defaultZ);
}
This function accepts a function with three double arguments that returns a double value, and a double value that will be the fixed last argument. Then it returns a new function with two double parameters that just passes two arguments and a fixed value to the original function.
Now you can apply the default value and use the returned 2D distance function:
Func<double, double, double> distance2D = distance3D.SetDefaultArgument(0);
var d1 = distance2D(3, 6);
var d2 = distance2D(3, 4);
var d3 = distance2D(1, 2);
You can apply any altitude. As an example, instead of the points on altitude z=0, you might want to work with the points at altitude z=3 as shown in the following figure:

We can use the same distance3D function by setting the default argument to 3. The code is shown in the following listing:
Func<double, double, double> distance2D_atLevel = distance3D.SetDefaultArgument(3);
var d1 = distance2D_atLevel(3, 6);
var d2 = distance2D_atLevel(3, 3);
var d3 = distance2D_atLevel(1, 1);
var d4 = distance2D_atLevel(0, 6);
If you need a single dimension function, you can create another function extension that converts the two argument function to a single argument function:
static Func<T1, TResult> SetDefaultArgument<T1, T2, TResult>
(this Func<T1, T2, TResult> function, T2 defaultY)
{
return x => function(x, defaultY);
}
This higher-order function is similar to the previous one but it uses a two-argument function and returns a single-argument function. Here are some examples of how you can use this single value function:
Func<double, double> distance = distance2D.SetDefaultArgument(3);
var d1 = distance(7);
var d2 = distance(3);
var d3 = distance(0);
distance = distance3D.SetDefaultArgument(2).SetDefaultArgument(4);
double d4 = distance(12);
double d5 = distance(-5);
double d6 = distance(-2);
In this example, we are creating a single argument function Distance. We can create this function either by setting a default parameter value to the two-parameter distance2D function, or by setting two default values to the three-argument function distance3D. In both cases, we will get a function with one argument. As you can see, parameter partitioning is a good way to slice your functions.
Curry Functions
In the previous example, how you can transform a function by reducing the number of arguments by one is shown. If you want to break it further, you will need to create another higher order function for partitioning. Currying is another way to transform a function by breaking an N-argument function to N single argument calls using a single higher-order function.
As an example, imagine that you have a function that extracts the substring of a string using the start position and length. This method might be called as in the following example:
var substring = mystring.Substring(3,5);
It would be more convenient if you would have two single argument functions instead of one two argument function and the call would look like:
var substring = mystring.Skip(3).Take(5);
With two single argument functions, you have more freedom to use and combine functions. As an example, if you need a substring from the third character to the end, you will use just the Skip(3) call. If you need just the first five characters of the string, you will call only Take(5) without Skip. In the original function, you will need to pass the default arguments for start or length even if you do not need them, or to create various combinations of the Substring function where the first argument will be defaulted to 0 and the second defaulted to length.
Currying is a method that enables you to break an N-argument function to N single argument calls. In order to demonstrate currying, here we will use the same 3D Distance function as in the previous example:
static double Distance(double x, double y, double z)
{
return Math.Sqrt(x * x + y * y + z * z);
}
Now we will use the following generic higher-order function for breaking three parameter functions to a list of single argument functions:
static Func<T1, Func<T2, Func<T3, TResult>>> Curry<T1, T2,
T3, TResult>(Func<T1, T2, T3, TResult> function)
{
return a => b => c => function(a, b, c);
}
This function will break the three argument function into a set of three single argument functions (monads). Now we can convert the Distance function to the curried version. We would need to apply the Curry higher-order function with all double parameters:
var curriedDistance = Curry<double, double, double, double>(Distance);
double d = curriedDistance(3)(4)(12);
Also, you can see how the function is called. Instead of the three argument function distance (3, 4, 12), it is called as a chain of single argument functions curriedDistance(3)(4)(12). In this example, a separate function that returns the curried version of the original function is used, but you might create it as an extension method. The only thing you need to do is put it in a separate static class and add the this modifier in the first argument:
public static Func<T1, Func<T2, Func<T3, TResult>>>
CurryMe<T1, T2, T3, TResult>(this Func<T1, T2, T3, TResult> function)
{
return a => b => c => function(a, b, c);
}
Now you can curry the function with a more convenient syntax (like a method of the function object without explicitly defined types):
Func<double, double, double, double> fnDistance = Distance;
var curriedDistance = fnDistance.CurryMe();
double d = curriedDistance(3)(4)(12);
Only note that you can apply this extension to the function object (fnDistance). Here, we will demonstrate the usage of the curry function in the same example as in the previous section - reducing three dimensional space.
Example - Reducing Spatial Dimensions
With one curried function, you can easily derive any function with a lower number of arguments. As an example, imagine that you want to create a two-dimensional distance function that calculates the distances of the points on altitude z=3 as shown in the following example:

In order to derive a function that works only with points at the altitude z=3, you will need to call the curried distance with parameter (3), and as a result, you will have a 2D function for determining the distances on that level. An example is shown in the following listing:
Func<double, Func<double, double>> distance2DAtZ3 = curriedDistance(3);
double d2 = distance2DAtZ3(4)(6);
double d3 = distance2DAtZ3(0)(1);
double d4 = distance2DAtZ3(2)(9);
double d5 = distance2DAtZ3(3)(4);
If you need a single argument distance function that calculates the distance of points at y=4 and z=3, you can slice the 2D function distance2DAtZ3 with an additional argument:
Func<double, double> distance1DAtY4Z3 = distance2DAtZ3(4);
double d6 = distance1DAtY4Z3(-4);
double d7 = distance1DAtY4Z3(12);
double d8 = distance1DAtY4Z3(94);
double d9 = distance1DAtY4Z3(10);
If you have not already sliced the function distance2DAtZ3, you can directly apply two default arguments on the original curried function:
Func<double, double> distance1DAtY4Z3 = curriedDistance(4)(3);
double d6 = distance1DAtY4Z3(-4);
double d7 = distance1DAtY4Z3(12);
double d8 = distance1DAtY4Z3(94);
double d9 = distance1DAtY4Z3(10);
As you can see, currying enables you to easily reduce the number of arguments of a multi-value function with just a single generic higher-order function, instead of writing several partial functions for each argument that should be reduced, as in the previous example.
Uncurrying
You can also use a higher order function to revert the curried function back. In this case, the curried version with several single arguments will be converted back to a multi-argument function. An example of the extension method that uncurries the three argument curry function is shown in the following listing:
public static Func<T1, T2, T3, TR> UnCurry<T1, T2, T3, TR>(
this Func<T1, Func<T2, Func<T3, TR>>> curriedFunc)
{
return (a, b, c) => curriedFunc(a)(b)(c);
}
This function accepts the curried version of the function and creates a new three-argument function that will call the curried function in single-argument mode. An example of usage of the Uncurry method is shown in the following listing:
var curriedDistance = Curry<double, double, double, double>(Distance);
double d = curriedDistance(3)(4)(12);
Func<double, double, double, double> originalDistance = curriedDistance.UnCurry();
d = originalDistance(3, 4, 12);
Conclusion
In this article, we saw some basic possibilities of functional programming in C#. Functional programming is a much wider area and cannot be explained in a single article. Therefore, there are a lot of other concepts in C# that you might need to explore in order to be capable of creating more effective functional programming code. Some of these concepts are expression trees, lazy evaluations, caching, etc. Also, you might find how functional programming is done in other languages such as F# or Haskel. Although C# does not have the same possibilities like these languages, you might find some ideas about how to write more effective functional constructions. In order to cover everything in functional programming, a whole book might be written about this topic, but I believe that I have succeeded in covering the most important aspects in this article.
Also, you can take a look at the comments section below where are posted a lot of examples (thanks to Akram for most of them) about the lazy evaluation, multiple inheritance, visitor design pattern implementation, folding, etc. I'm adding shorter versions of these examples in this article but you can find a lot of complete examples about these topics in comments.
You can also see some great examples of functional programming in the Data-driven programming combined with Functional programming in C# article.
History
I'm constantly improving this article with help of other such as Akram and noav who are posting interesting examples and suggestions in the comments section. Here, you can see information about the major changes done in the article.
- 11th May, 2012 - Closures. Added section where closures in functional programming are described.
- 12th May, 2012 - Caching. Added an example of caching values in the closure section based on the noav idea with Memoize extension
