Introduction
This article is intended to introduce software
developers into the topic of optimization techniques. For this, different optimization techniques will be explored.
As
a first step, I have chosen an easy to
understand algorithm to which I have applied various optimization techniques:
The problem we will solve is the 3n + 1 problem (details): for every number n between 1 and 1000000 apply the following function:
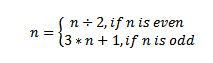
until the number becomes 1, counting the number of time we applied the function.
This
algorithm will be executed for all the numbers between 1 and 1000000. No input
number from the keyboard will be read and the program will print the result,
followed by the execution time (in milliseconds) needed to compute the result.
Test machine will be a laptop with the following specs: AMD Athlon 2 P340 Dual Core 2.20 GHz, 4 GB of RAM, Windows 7 Ultimate x64.
Languages used for implementation: C# and C++ (Visual Studio 2010).
Prerequisite
N/A
Different
implementations for the same problem
The
initial version of implementation: for each number between 1 and 1000000, the above
mentioned algorithm will be applied, generating a sequence of numbers until n
becomes 1. The steps needed to reach to 1 will be counted
and the maximum number of steps will be determined.
C++ code:
for (int i = nFirstNumber; i < nSecondNumber; ++i)
{
int nCurrentCycleCount = 1;
long long nNumberToTest = i;
while (nNumberToTest != 1)
{
if ((nNumberToTest % 2) == 1)
{
nNumberToTest = nNumberToTest * 3 + 1;
}
else
{
nNumberToTest = nNumberToTest / 2;
}
nCurrentCycleCount++;
}
if (nCurrentCycleCount > nMaxCycleCount)
{
nMaxCycleCount = nCurrentCycleCount;
}
} C# code:
for (int i = FirstNumber; i < SecondNumber; ++i)
{
int iCurrentCycleCount = 1;
long iNumberToTest = i;
while (iNumberToTest != 1)
{
if ((iNumberToTest % 2) == 1)
{
iNumberToTest = iNumberToTest * 3 + 1;
}
else
{
iNumberToTest = iNumberToTest / 2;
}
iCurrentCycleCount++;
}
if (iCurrentCycleCount > MaxCycleCount)
{
MaxCycleCount = iCurrentCycleCount;
}
} I compiled the code for both Debug and Release builds, both 32 bit and 64 bit version. I then ran every executable 100 times and computed the average time(ms) it takes to do the calculations.
Here are the results:
| C++ Debug | C++ Release | C# Debug | C# Release |
| x86 version | 6882.91 | 6374.50 | 6358.41 | 5109.90 |
| x64 version | 1020.78 | 812.71 | 1890.36 | 742.28 |
First thing to be observed in the table is that
the 32 bits program versions are 5 to 7 times slower than the 64 bits versions.
This is due to the fact that on x64 architectures one register can hold a long long variable and on x86 we need 2 registers. This means that on x86 operations with long long values are slow. Because of this we will not examine the 32 bits anymore in this
article.
Second thing to be noticed is the difference
between Release and Debug builds and, also, that for C# the differences are
bigger than for C++.
Another
observation is the difference between the C# Release version and C++ Release
version. This, together with the previous observation, makes me believe that the
C# compiler performs optimization better than the C++ compiler (maybe even
employing some of the optimization techniques we are going to talk about
later).
The
first optimizations I will apply are related to performing the mathematical
operations faster by replacing the conventional way of doing them with an
unconventional way.
If
we look at the above code we see that we have only 3 complex mathematical
operations: modulo 2 operation(%),
multiplication by 3(*) and division by 2(/).
First operation I will optimize is the modulo 2.
We know that all numbers are represented in memory as a sequence of bits. we
also know, the representation of an odd number will always have its last bit 1(5
= 101, 13 = 1101, etc.) and the representation of an even number will always
have its last bit 0( 6 = 110, 22 = 10110). So if we can get the last bit of a
number and test it against 0 we know if a number is odd or even. To get the
last bit of a number I use the bitwise AND operator(&).
In C++, replace:
if ((nNumberToTest % 2) == 1)
with:
if ((nNumberToTest & 0x1) == 1)
In C#, replace:
if ((iNumberToTest % 2) == 1)
with:
if ((iNumberToTest & 0x1) == 1)
Here are the results:
| C++ Debug | C++ Release | C# Debug | C# Release |
| 922.46 | 560.86 | 1641.41 | 714.10 |
C++
Release version benefits most from this optimization. The difference in
improvement between the C++ Release and Debug versions leads me to believe that
the compiler is able to remove more instructions in the Release build with the
new optimization algorithm.
C#
seems not to benefit too much from this optimization.
The
next operation I will try to optimize is the division by 2. If we look again at
the binary representation of the numbers, we can observe that when we divide by
2 we discard the last bit of the number and we add a 0 bit before the remaining
bits. So 5 (=101) / 2 = 2 (=010), 13 (=1101) / 2 = 6 (=0110), 6 (=110) / 2 = 3
(= 011), etc. I will replace this operation with the bitwise right shift
operation that produces the same result.
In C++, replace:
nNumberToTest = nNumberToTest / 2;
with:
nNumberToTest = nNumberToTest >> 1;
In C#, replace:
iNumberToTest = iNumberToTest / 2;
with:
iNumberToTest = iNumberToTest >> 1;
Here are the results:
| C++ Debug | C++ Release | C# Debug | C# Release |
| 821.58 | 555.96 | 1432.01 | 652.11 |
C++
Debug, C# Debug, C# Release version gain between 65 and 200 milliseconds from
this optimization.
C++
Release gains almost nothing from this replacement probably because the
compiler was already performing this optimization.
Last
mathematical operation that consumes time is the multiplication by 3. The only
thing we can do to this operation is to replace it by additions.
In C++ replace:
nNumberToTest = nNumberToTest * 3 + 1;
with:
nNumberToTest = nNumberToTest + nNumberToTest + nNumberToTest + 1;
In C# replace:
iNumberToTest = iNumberToTest * 3 + 1;
with:
iNumberToTest = iNumberToTest + iNumberToTest + iNumberToTest + 1;
Here are the results:
| C++ Debug | C++ Release | C# Debug | C# Release |
| 820.84 | 548.93 | 1535.28 | 629.89 |
The
biggest performance gain can be observed in the C# Release version, followed by
the C++ Release version.
C# Debug version shows a decreased performance due
to the fact that the current software version executes more instructions than
the previous one and the compiler can not optimize the instructions (it can not
replace them with anything else because we might need to set a break point on any of them).
There
is one last mathematical optimization we can perform based on some special instructions that the
processor implements. These instructions are the so-called conditional move
instructions. To determine the compiler to generate a conditional move
instruction, I will replace the IF statement (which checks if the number is odd
or even) with the ternary operator( ?: ).
To
be able to implement the optimization mentioned above we need to modify the
problem statement. If the number is even, it will be divided by 2 (as imposed
for the problem). If the number is odd then it can be expressed as 2 * n + 1. Applying
this modifications to the initial form of the function we will obtain:

From the above equation we can see that we can perform
2 steps of the algorithm into 1. We will rewrite the algorithm so that we
compute next value of the number to test, assuming the current value is even.
Then we will save the value of the last bit of the current number to test. If
this value is true, we will increment the current cycle count and add the current
number + 1 to the next value of the number to test. (Note: this optimization
will become really important in one of the next articles when I will talk about
SSE).
In C++ replace:
if ((nNumberToTest % 2) == 1)
{
nNumberToTest = nNumberToTest * 3 + 1;
}
else
{
nNumberToTest = nNumberToTest / 2;
}
nCurrentCycleCount++;
with:
int nOddBit = nNumberToTest & 0x1;
long long nTempNumber = nNumberToTest >> 1;
nTempNumber += nOddBit?nNumberToTest + 1:0;
nCurrentCycleCount += nOddBit?2:1;
nNumberToTest = nTempNumber;
In C# replace:
if ((iNumberToTest % 2) == 1)
{
iNumberToTest = iNumberToTest * 3 + 1;
}
else
{
iNumberToTest = iNumberToTest / 2;
}
iCurrentCycleCount++;
with:
bool bOddBit = (iNumberToTest & 0x1) == 0x1;
long iTempNumber = iNumberToTest >> 1;
iTempNumber += bOddBit ? iNumberToTest + 1 : 0;
iCurrentCycleCount += bOddBit ? 2 : 1;
iNumberToTest = iTempNumber;
Here are the results:
| C++ Debug | C++ Release | C# Debug | C# Release |
| 1195.38 | 462.21 | 1565.01 | 752.92 |
Both debug builds show a slowdown, because we
are now executing more instructions compared to the previous versions of the
code and the compilers can not optimize them.
The
C# Release version shows a slowdown because there are no conditional move
instructions in C#.
The
power of this category of instructions is proved by the increased speed of the
C++ Release version.
It
can be noticed the I did solve the problem using recursion. For this problem, a
recursive algorithm would be extremely slow: the maximum cycle length is 525,
so assuming that most of the numbers have a cycle length of around 150 (just a guess,
not actually verified), if we have 150 recursive calls for every number between
1 and 1000000, we would have to perform 150000000 calls. This, clearly, is not
a small number and, because calling a function takes a lot of time, recursion is,
definitely, not a good solution for this problem.
Points of Interest
It's
time to draw the conclusions:
- Modulo and division operation take a lot of time and they should be replaced by
something else.
- Try to analyze the problem and obtain an alternate representation of the
problem.
- Try to eliminate the IF statements from your code in the case that their only
purpose is to set some values based on a condition.
The
next time topic will be about how to make our program faster, using threading
in C# and C++.
History
- 27 May 2012 - Initial release.
- 28 May 2012 - I would like to thank anlarke for pointing out things that could be improved in the article and for submitting his code (C++ Debug time: 546.76 ms, C++ Release time: 386.35 ms). Also I would like to thank Reonekot for his clarification on the WoW topic. He is right and the performance problems are caused by the fact that the registers are 32 bits (for x86) and 64 bits (for x64).
