Generating Keys for a Custom Sort Order

• Download Sources

Introduction

Brief:To represent a user defined sort order in a relational database, we need to generate values for a "sort order" column that we can use for ORDER BY. How do we generate those values?

Relational databases offer a possibility to order data by a given column or expression - e.g. ORDER BY Name in SQL. They usually do not support storing a user defined sort order. To represent such a sort order, we usually introduce an integer column. However, an integer field might require renumbering fairly often - i.e. having to reassign all (or many) of the columns, even though only one or a few items have changed their position or were inserted.

This article shows an alternate approach, generating strings that trades (an reasonable amount of) storage for avoiding the need to renumber, or at least delay it significantly.

Note: I'm not perfectly happy with the solution. The final code is a bit experimental still. It provides what I need, but I can't shed the feeling that I'm missing an obvious simplification.  I'll try to make up for that by a brain dump of finding that solution, which might be interesting for some.

The traditional solution

A simple solution is to use integers for the sort key column, and assign incremental values in the order we want the items to be. This poses a little problem however:

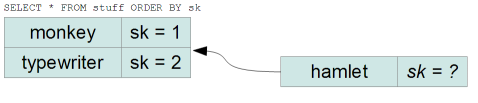
what sort key should hamlet get?

Usually, you assign the numbers with gaps, e.g. 10 for monkey and 20 for typewriter, so hamlet could get 15. However, after a finite (and often very small) number of inserts, we are back to the problem above: there is no integer between N and N+1.

The solution to that problem usually is to "renumber" the items: assign new sort keys for all or at least for multiple items.

Can we generate sort keys that affect only the item inserted?

Constructing a different solution

Core idea: Looking at above image, it is suggests itself to use real values instead of integers, and assign 1.5 (the average of 1 and 2) as sort key to hamlet.

First analysis: Using IEEE 754 floating point values, as they are supported by most systems, has some problems, though, the main problem being limited accuracy. A double, with 53 bits, may lose precision after only 54 badly placed inserts. To make things worse, this happens silently, do it would need to be detected explicitly.

A minor problem is how to add items at front or at the end of the list. It would be simple to use (minimum - 1) or (maximum + 1) respectively, but that would easily make the precision problem worse.

If I had a hammer: All these problems would be solved at least in principle if we had an unlimited precision "bignum" type available. However, we usually don't, and even if, the precision problems would usually be solved by requiring more storage.

A possible solution would be to implement arbitrary precision numbers with only the operations increment, decrement, average of two, and compare. This seemed simple, however finding a representation where the compare would be a simple string comparison (or something similar commonly available) troubled me most.

At this point, I felt pretty stuck, and pondered different minor variations for a while. Good thing the solution wasn't urgent, I could keep it in the back of my mind for a few days.

Revelation: Since I was stuck with the representation, I ignored that problem for a while, focusing on the simpler calculation of an average, already fleshing out  some minor details: instead of strings consisting of the digits '0' .. '9', I could use the entire letter space. I could use the ASCII characters '!' == 33 ... '~' == 126 for base-94 numbers. When calculating the average,  I wouldn't have to be particularly exact, I could truncate trailing digits if my "almost average" was somewhere between the two sort keys specified. This could limit the possibly excessive growth in number of digits required when inserts happen on the same place. For the experiments with the algorithms, I simply used some "guard values" before and after the actual list, so all operations would be inserts between two values. Since I didn't care about the "-1" and "+1" for now, I focused only on the digits after the decimal point, which made the strings simple to compare.

It took me a while to notice I had already solved my problem.

1. Keeping all values between two arbitrary guard values, the only operation I needed was average of two values:

2. Keeping all values between 0 and 1 would allow a simple string representation of the post-decimal positions, where a string comparison is almost identical to a numeric comparison (with some exceptions except for some corner cases that don't matter for our purpose):

What suddenly hit me wasn't the solution itself, but the realization that I already held the solution in my hands (and had made my silly little tests with it for longer than I am comfortable to admit). This feeling is a light bulb supernova and at the same time incredibly humbling.

Tinkering: I still had to tinker with the solution a lot, more than I expected. I ended up implementing an "almost increment" and "almost decrement" do deal with the prefix / append case which are common operations, but were pathological, as they would increase the string length rapidly. I still have two branches that I think will never be taken (and in my tests never are), but I'm hesitant to take out because I can't prove that. I've tinkered with the different cases and some constants (such as by how many "digits" to expand a string) to avoid excessive string growth. I tried to construct various pathological cases to make that rather heuristically derived algorithm more robust.

The Solution

Sort keys are strings that represent the post-decimal digits of a rational number, for which a string comparison is very similar to the numeric comparison, and can be used if some constraints are observed.

A trivial mapping from the decimal system would use '0' .. '9' as characters. The examples here use 'a' .. 'z', since this is somewhat mroe illustrative. The actual implementation can use any consecutive range of characters (provided it's more than 3 elements).

The strings may not end in 'a', since there is no string you can put between "x" and "xa".

Three operations are implemented for these values:

CStringA Before(CStringA const & v)

Returns a value that compares less than v.

In most cases, it is a simple decrement:

Before("abc")  == "abb"<br>
Before("abb")  == "aaz"    (do not end in 'a' rule)<br>
Before("ab")   == "aaz"    (

ince 
this cannot be decremented further, expand. Think of 0.009 < 0.01)

In practice, we append more than one 'z', to prevent excessive growth when always inserting before the first element:
If appending only one 'z', we could only "decrement" 25 times before having to append once. By appending "zz", we can decrement 26*25 times before having to expand, by appending "zzz" we can decrement 26*26*25 times.

CStringA After(CStringA const & v)

Returns a value that compares greater than v.

In most cases, it is a simple increment:

Before("abc")  == "abd"<br>
Before("abz")  == "acb"     (again, do not end in 'a' 
rule)<br>
Before("zzz")  == "zzzab"   (

Again, in practice, we append more than one character, and we have to observe the don't end in 'a' rule, so we append "ab".

CStringA Between(CStringA const & a, CString const & b)

Returns a value that compares greater than a and less than  b.

The implementation is a bit more complex, for details see the implementation.

The Tests

Besides some unit(ish) tests on specific values, I ran various operations to check against excessive growth, the effect of some parameters, and various possibly pathological cases.

The tests always consist of 5 sequential start values "m" .. "q", and (up to) 100000 of the following operations:

• insert before all values
• insert after all values
• insert between two values at a random position
• delete a random value
• insert at a fixed position (between index 6 and 7)

The tests give percentages of these operations. Note that the percentages not always add up to 100, due to display rounding.

Baseline Test

The base line test uses a "healthy mix" of the different operations, and ends up with a maximum length of the sort key of 22. Not bad for a vector of 100005 values and a wild monkey user.

"Expand By" indicates the number of characters appended to a string when the length (i.e. precision) needs to be increased.

Insert Only

To the left is the "healthy mix" base line test, to the right the test with only inserts. We are not as good for random inserts as for sequential ones, but still not bad.

Expanding the character set

Surprisingly, extending the character set from 26 to 94 characters makes no difference in the maximum length. However, as the last column shows, increasing the character set allows to reduce the expand length.

Increasing the expand by length to 4 does not significantly increase the length of the generated keys (from 22 to 29).

With the smaller character set 'a'-'z', decreasing the expand by length causes a significant increase in the length of the sort key to a maximum of 113. Still acceptable, already pointing towards the previously observed aggressive growth.

With an extended char set, reducing the expand by length actually also decreases the maximum sort key length.

This suggests that sequential inserts with a short "expand by" length may become critical, while a slightly longer "expand by" length is more stable (though it gets a bit worse for random inserts).

The optimal "expand by" length depends on the character range, the total number of items expected and of course the insert pattern. However, 3 seems to yield acceptable results over a wide range of inputs.

An "expand by" length that is adaptive to the current sort key length might even be more adaptive, but appears to be not necessary.

Further test results are available in the sources, but they are not particularly interesting.

Critical Review

It is not clear whether this effort is really necessary for the application in question. Rarely any user will want to manually assign a sort order to 100K items, and for automatically generated data, usually a timestamp or similar sort criterion is available.

For typical use cases where the user may want to provide a specific order, 20..30 items may already be considered many, and an integer-based scheme with enough space between the items may be sufficient. With frequent inserts and moves, renumbering the items may occasionally become necessary, but is unlikely to have problematic performance.

The algorithm may have a significant application if very many items are affected, or modifying more than one row is not just a performance but possibly a concurrency, locking or API problem.

History

Sept 5, 2012: published