Introduction
Brief:To represent a user defined sort order in a
relational database, we need to generate values for a "sort order" column that
we can use for ORDER BY. How do we generate those values?
Relational databases offer a possibility to order data by a given column or
expression -
e.g. ORDER BY Name in SQL. They usually do not support storing a
user defined sort order. To represent such a sort order, we usually introduce an
integer column. However, an integer field might require renumbering
fairly often - i.e. having to reassign all (or many) of the columns, even though
only one or a few items have changed their position or were inserted.
This article shows an alternate approach, generating strings that trades (an
reasonable amount of) storage for avoiding the need to renumber, or at least
delay it significantly.
Note: I'm not perfectly happy with the solution. The final code is a bit
experimental still. It provides what I need, but I can't shed the feeling that
I'm missing an obvious simplification. I'll try to make up for that by a
brain dump of finding that solution, which might be interesting for some.
The traditional solution
A simple solution is to use integers for the sort key column, and assign
incremental values in the order we want the items to be. This poses a little
problem however:
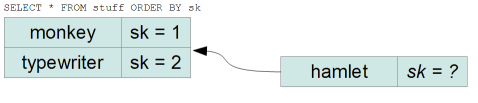
what sort key should hamlet get?
Usually, you assign the numbers with gaps, e.g. 10 for monkey and 20 for
typewriter, so hamlet could get 15. However, after a finite (and often very
small) number of inserts, we are back to the problem above: there is no integer
between N and N+1.
The solution to that problem usually is to "renumber" the items: assign new
sort keys for all or at least for multiple items.
Can we generate sort keys that affect only the item inserted?
Constructing a different solution
Core idea: Looking at above image, it is suggests itself to
use real values instead of integers, and assign 1.5 (the average of 1 and 2) as
sort key to hamlet.
First analysis: Using IEEE 754 floating point values, as
they are supported by most systems, has some problems, though, the main problem
being limited accuracy. A double, with 53 bits, may lose precision
after only 54 badly placed inserts. To make things worse, this happens silently,
do it would need to be detected explicitly.
A minor problem is how to add items at front or at the end of the list. It
would be simple to use (minimum - 1) or (maximum + 1) respectively, but that
would easily make the precision problem worse.
If I had a hammer: All these problems would be solved at
least in principle if we had an unlimited precision "bignum" type available.
However, we usually don't, and even if, the precision problems would usually be
solved by requiring more storage.
A possible solution would be to implement arbitrary precision numbers with
only the operations increment, decrement, average of two, and compare. This
seemed simple, however finding a representation where the compare would be a
simple string comparison (or something similar commonly available) troubled me
most.
At this point, I felt pretty stuck, and pondered different minor variations
for a while. Good thing the solution wasn't urgent, I could keep it in the back
of my mind for a few days.
Revelation: Since I was stuck with the representation, I
ignored that problem for a while, focusing on the simpler calculation of an
average, already fleshing out some minor details: instead of strings
consisting of the digits '0' .. '9', I could use the entire letter space. I
could use the ASCII characters '!' == 33 ... '~' == 126 for base-94 numbers.
When calculating the average, I wouldn't have to be particularly exact, I
could truncate trailing digits if my "almost average" was somewhere between the
two sort keys specified. This could limit the possibly excessive growth in
number of digits required when inserts happen on the same place. For the
experiments with the algorithms, I simply used some "guard values" before and
after the actual list, so all operations would be inserts between two values.
Since I didn't care about the "-1" and "+1" for now, I focused only on the
digits after the decimal point, which made the strings simple to compare.
It took me a while to notice I had already solved my problem.
1. Keeping all values between two arbitrary guard values, the only
operation I needed was average of two values:

2. Keeping all values between 0 and 1 would allow a simple string
representation of the post-decimal positions, where a string comparison is
almost identical to a numeric comparison (with some exceptions except for some
corner cases that don't matter for our purpose):

What suddenly hit me wasn't the solution itself, but the realization that
I already held the solution in my hands (and had made my silly little tests
with it for longer than I am comfortable to admit). This feeling is a light bulb
supernova and at the same time incredibly humbling.
Tinkering: I still had to
tinker with the solution a lot, more than I expected. I ended up implementing an
"almost increment" and "almost decrement" do deal with the prefix / append case
which are common operations, but were pathological, as they would increase the
string length rapidly. I still have two branches that I think will never be
taken (and in my tests never are), but I'm hesitant to take out because I can't
prove that. I've tinkered with the different cases and some constants (such as
by how many "digits" to expand a string) to avoid excessive string growth. I
tried to construct various pathological cases to make that rather heuristically
derived algorithm more robust.
The Solution
Sort keys are strings that represent the post-decimal digits of a rational
number, for which a string comparison is very similar to the numeric comparison,
and can be used if some constraints are observed.
A trivial mapping from the decimal system would use '0' .. '9' as characters.
The examples here use 'a' .. 'z', since this is somewhat mroe illustrative. The
actual implementation can use any consecutive range of characters (provided it's
more than 3 elements).
The strings may not end in 'a', since
there is no string you can put between "x" and "xa".
Three operations are implemented for these values:
CStringA Before(CStringA const & v)
Returns a value that compares less than v.
In most cases, it is a simple decrement:
Before("abc") == "abb"<br>
Before("abb") == "aaz" (do not end in 'a' rule)<br>
Before("ab") == "aaz" (s
ince
this cannot be decremented further, expand. Think of 0.009 < 0.01)
In practice, we append more than one 'z', to prevent excessive
growth when always inserting before the first element:
If appending only one 'z', we could only "decrement" 25 times before having to
append once. By appending "zz", we can decrement 26*25 times before having to
expand, by appending "zzz" we can decrement 26*26*25 times.
CStringA After(CStringA const & v)
Returns a value that compares greater than v.
In most cases, it is a simple increment:
Before("abc") == "abd"<br>
Before("abz") == "acb" (again, do not end in 'a'
rule)<br>
Before("zzz") == "zzzab" (cannot
incremented further, expand. Think of 0.99901 > 0.999)
Again, in practice, we append more than one character, and we have to observe
the don't end in 'a' rule, so we append "ab".
CStringA Between(CStringA const & a, CString const & b)
Returns a value that compares greater than a and
less than b.
The implementation is a bit more complex, for details see the implementation.
The Tests
Besides some unit(ish) tests on specific values, I ran various operations to
check against excessive growth, the effect of some parameters, and various
possibly pathological cases.
The tests always consist of 5 sequential start values "m" .. "q", and (up to)
100000 of the following operations:
- insert before all values
- insert after all values
- insert between two values at a random position
- delete a random value
- insert at a fixed position (between index 6 and 7)
The tests give percentages of these operations. Note that the percentages not
always add up to 100, due to display rounding.
Baseline Test
The base line test uses a "healthy mix" of the different operations, and ends
up with a maximum length of the sort key of 22. Not bad for a vector of 100005
values and a wild monkey user.
Character set
insert before
insert between
insert after
delete
insert @ Index 7
Expand By
MaxLen
| 'a' - 'z'
18%
37%
36%
9%
0%
3
22 |
"Expand By" indicates the number of characters appended to a string when the
length (i.e. precision) needs to be increased.
Insert Only
Character set
insert before
insert between
insert after
delete
insert @ Index 7
Expand by
MaxLen
| 'a' - 'z'
18%
37%
36%
9%
0%
3
22 | | 'a' - 'z'
0%
100%
0%
0%
0%
3
43 | |
To the left is the "healthy mix" base line test, to the right the test with
only inserts. We are not as good for random inserts as for sequential ones, but
still not bad.
Expanding the character set
Character set
insert before
insert between
insert after
delete
insert @ Index 7
Expand by
MaxLen
| 'a' - 'z'
18%
37%
36%
9%
0%
3
22 | | '!' - '~'
18%
37%
36%
9%
0%
3
22 | | 'a' - 'z'
18%
37%
36%
9%
0%
4
29 | | 'a' - 'z'
18%
37%
36%
9%
0%
2
113 | | '!' - '~'
18%
37%
36%
9%
0%
2
15 | |
Surprisingly, extending the character set from 26 to 94 characters makes no
difference in the maximum length. However, as the last column shows, increasing
the character set allows to reduce the expand length.
Increasing the expand by length to 4 does not significantly increase the
length of the generated keys (from 22 to 29).
With the smaller character set 'a'-'z', decreasing the expand by length
causes a significant increase in the length of the sort key to a maximum of 113.
Still acceptable, already pointing towards the previously observed aggressive
growth.
With an extended char set, reducing the expand by length actually also
decreases the maximum sort key length.
This suggests that sequential inserts with a short "expand by" length may
become critical, while a slightly longer "expand by" length is more stable
(though it gets a bit worse for random inserts).
The optimal "expand by" length depends on the character range, the total
number of items expected and of course the insert pattern. However, 3 seems to
yield acceptable results over a wide range of inputs.
An "expand by" length that is adaptive to the current sort key length might
even be more adaptive, but appears to be not necessary.
Further test results are available in the sources, but they are not
particularly interesting.
Critical Review
It is not clear whether this effort is really necessary for the application
in question. Rarely any user will want to manually assign a sort order to 100K
items, and for automatically generated data, usually a timestamp or similar sort
criterion is available.
For typical use cases where the user may want to provide a specific order,
20..30 items may already be considered many, and an integer-based scheme with
enough space between the items may be sufficient. With frequent inserts and
moves, renumbering the items may occasionally become necessary, but is unlikely
to have problematic performance.
The algorithm may have a significant application if very many items are
affected, or modifying more than one row is not just a performance but possibly
a concurrency, locking or API problem.
History
Sept 5, 2012: published
