Sometimes, it is useful to convert a transformation with a non-zero center point to an equivalent transformation with a zero center point. If you find you have a need for this, then maybe this post will be helpful.
Posts in this series:
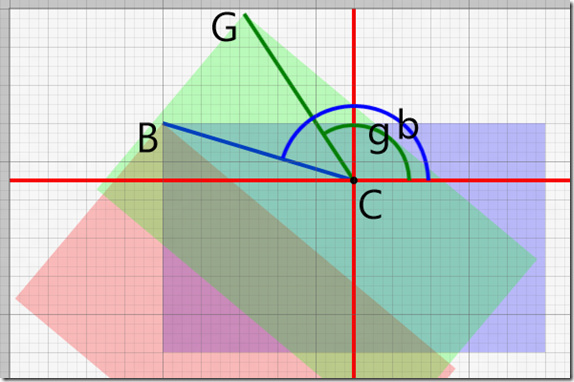
Consider this diagram:
In the above drawing, the green rectangle is translated Tx=80, Ty=60, and rotated R=40° about the center Cx=100, and Cy=30. The goal of this post is to come up with an equivalent transformation with a center point of Cx=0, Cy=0.
The first step is to apply only the translation of Tx=80, Ty=60 and see where that gets us. The result of that is the blue rectangle.
The next step is to apply the rotation of R=40° about the center at Cx=0, Cy=0. The result of that is the red rectangle.
Our last step is to adjust the translation of Tx and Ty to move point B to point G. That is, if we know Bx, By, Gx, and Gy then the new translation is:
- Tx = 80 + Gx – Bx
- Ty = 80 + Gy – By
This will require a bit of trigonometry.
Point C is the center point of the rotation of the blue and green rectangles. The distance from C to B is the same as the distance from C to G. That is, the distance CB = CG. For simplicity, we will call this distance d. Clearly:
Now let’s imagine point C is at 0,0 (but let’s keep the original values of Cx=100 and Cy=30 for the rest of the calculations). If that is the case, then:
- Bx = -Cx
- By = -Cy
- Gx = \cos(g).d
- Gy = \sin(g).d
Once we determine the angles b and g, we are done. Determining the first angle b is easy:
- b = \text{atan2}(-Cy,-Cx)
The second angle g is even easier:
So let’s work this problem through:
- d = \sqrt{Cx^2 + Cy^2} = \sqrt{100^2 + 30^2} = 104.4
- b = \text{atan2}(-Cy,-Cx) = \text{atan2}(-30,-100) = -163.3°
- g = b + R = -163.3° + 40° = -123.3°
- Bx = -Cx = -100
- By = -Cy = -30
- Gx = Cos(g) * d = \cos(-123.3°) * 104.4 = -57.3
- Gy = Sin(g) * d = \sin(-123.3°) * 104.4 = -87.3
- Tx = Tx + Gx -Bx = 80 + (-57.3) - (-100) = 122.7
- Ty = Ty + Gy -By = 60 + (-87.3) - (-30) = 2.7
Here is an overlay of the before (green) and after (blue) transformations:

Here is the XAML that overlays both transformations:
ZeroCtrPtExample.xaml
<Page
x:Class="PanViewDemoApp.ZeroCtrPtExample"
IsTabStop="false"
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
xmlns:local="using:PanViewDemoApp"
xmlns:d="http://schemas.microsoft.com/expression/blend/2008"
xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"
mc:Ignorable="d"
FontSize="16">
<Canvas>
<Border
Height="120"
Width="200"
Background="LightGreen">
<Border.RenderTransform>
<CompositeTransform
x:Name="M"
TranslateX="80"
TranslateY="60"
Rotation="40"
CenterX="100"
CenterY="30" />
</Border.RenderTransform>
<TextBlock
Margin="3"
Foreground="Green">Tx=80 Ty=60<LineBreak />
R=40<LineBreak />Cx=100 Cy=30</TextBlock>
</Border>
<Border
Height="120"
Width="200"
BorderThickness="3"
BorderBrush="Blue">
<Border.RenderTransform>
<CompositeTransform
x:Name="N"
TranslateX="122.7"
TranslateY="2.7"
Rotation="40" />
</Border.RenderTransform>
<TextBlock
VerticalAlignment="Bottom"
Foreground="Blue"
Margin="3">Tx=122.7 Ty=2.7<LineBreak />
R=40<LineBreak />Cx=0 Cy=0</TextBlock>
</Border>
</Canvas>
</Page>
Here is some C# code that performs the zeroing of the center point of a transformation:
TransformExtensions.cs
static void InternalZeroCenterPoint(ICompositeTransform t)
{
var d = Math.Sqrt(t.CenterX * t.CenterX + t.CenterY * t.CenterY);
var b = Math.Atan2(-t.CenterY, -t.CenterX);
var g = b + t.Rotation * Math.PI / 180;
var Bx = -t.CenterX;
var By = -t.CenterY;
var Gx = Math.Cos(g) * d;
var Gy = Math.Sin(g) * d;
t.TranslateX += Gx - Bx;
t.TranslateY += Gy - By;
t.CenterX = 0;
t.CenterY = 0;
}
