C# Implementation of Basic Linear Algebra Concepts

Introduction

I am sharing with you my C# implementation of the basic linear algebra concepts. The full code has been posted to GitHub (https://github.com/elsheimy/Elsheimy.Components.Linears) under the MIT license and Nuget (https://www.nuget.org/packages/Elsheimy.Components.Linears/). Feel free to modify and deal with code without any restrictions or limitations (no guarantees of any kind too). And please let me know your feedback, comments, suggestions, and corrections.

The code covers the following:

Matrices

• Matrix addition / subtraction
• Matrix concatenation / shrinking / extraction
• Matrix reduction and elimination (Gauss and Gauss-Jordan)
• Matrix rank, solution, and solution state (unique, infinite, and no solution)
• Determinant calculation using Laplace Expansion method
• Invertibility and inverses
• Matrix mirrors
• Matrix multiplication and powers
• Transposes
• Identity matrices
• Transformation matrices
• Projection matrices
• Reflection matrices
• 2D and 3D rotation matrices
• 2D and 3D shearing matrices
• Cloning and equality comparers

Vectors

• Vector addition / subtraction
• Angel between vectors
• Vector normalization and magnitude calculator
• Dot product and cross product
• Vector scaling
• Projection onto other vectors and subspaces
• Cloning and equality comparers

The design is based on raw functions that operate on Array objects. Wrapper classes for matrices and vectors (Matrix and Vector, respectively) have been created to hide those keen functions. Static initializers and operators have been added to simplify the use of the wrapper classes.

Quote:

I will not go into a discussion of how a function mathematically works. Despite this, feel free to correct me whenever you want.

Let’s have a brief look at some of the highlights of the code.

Matrices

Matrix Elimination

This function demonstrates Gaussian and Gauss-Jordan elimination. It can be used to reduce a matrix to the row-echelon form (REF / Gaussian) or reduced row-echelon form (RREF / Gauss-Jordan.) It can be used to solve a matrix for a number of augmented columns and to calculate matrix rank.

/// <summary>
/// Reduces matrix to row-echelon (REF/Gauss) or 
/// reduced row-echelon (RREF/Gauss-Jordan) form and solves for augmented columns (if any.)
/// </summary>
public static MatrixEliminationResult Eliminate(double[,] input, 
              MatrixReductionForm form, int augmentedCols = 0) {
  int totalRowCount = input.GetLength(0);
  int totalColCount = input.GetLength(1);

  if (augmentedCols >= totalColCount)
    throw new ArgumentException(nameof(augmentedCols),
      Properties.Resources.Exception_TooMuchAugmentedColumns);

  MatrixEliminationResult result = new MatrixEliminationResult();
  double[,] output = CreateCopy(input);
 
  // number of pivots found
  int numPivots = 0;
 
  // loop through columns, exclude augmented columns
  for (int col = 0; col < totalColCount - augmentedCols; col++) {
    int? pivotRow = FindPivot(output, numPivots, col, totalRowCount);
    if (pivotRow == null)
      continue; // no pivots, go to another column
    ReduceRow(output, pivotRow.Value, col, totalColCount);
    SwitchRows(output, pivotRow.Value, numPivots, totalColCount);
    pivotRow = numPivots;
    numPivots++;

    // Eliminate Previous Rows
    if (form == MatrixReductionForm.ReducedRowEchelonForm) {
      for (int tmpRow = 0; tmpRow < pivotRow; tmpRow++)
        EliminateRow(output, tmpRow, pivotRow.Value, col, totalColCount);
    }

    // Eliminate Next Rows
    for (int tmpRow = pivotRow.Value; tmpRow < totalRowCount; tmpRow++)
      EliminateRow(output, tmpRow, pivotRow.Value, col, totalColCount);
  }

  result.Rank = numPivots;
  result.FullMatrix = output;
  result.AugmentedColumnCount = augmentedCols;
  if (augmentedCols > 0 && 
      form == MatrixReductionForm.ReducedRowEchelonForm) { // matrix has solution
    result.Solution = ExtractColumns(output, totalColCount - augmentedCols, totalColCount - 1);
  }

  return result;
}

private static int? FindPivot(double[,] input, int startRow, int col, int rowCount) {
  for (int i = startRow; i < rowCount; i++) {
    if (input[i, col] != 0)
      return i;
  }

  return null;
}

private static void SwitchRows(double[,] input, int row1, int row2, int colCount) {
  if (row1 == row2)
    return;

  for (int col = 0; col < colCount; col++) {
    var tmpVal1 = input[row1, col];
    input[row1, col] = input[row2, col];
    input[row2, col] = tmpVal1;
  }
}

private static void ReduceRow(double[,] input, int row, int col, int colCount) {
  var coeffecient = 1.0 / input[row, col];

  if (coeffecient == 1)
    return;

  for (; col < colCount; col++)
    input[row, col] *= coeffecient;
}

/// <summary>
/// Eliminates row using another pivot row.
/// </summary>
private static void EliminateRow(double[,] input, int row, int pivotRow, 
                                 int pivotCol, int colCount) {
  if (pivotRow == row)
    return;

  if (input[row, pivotCol] == 0)
    return;

  double coeffecient = input[row, pivotCol];

  for (int col = pivotCol; col < colCount; col++) {
    input[row, col] -= input[pivotRow, col] * coeffecient;
  }
}

This function has been wrapped into our Matrix wrapper with those functions:

public virtual Matrix Reduce(MatrixReductionForm form, int? augmentedColCount = null);
public virtual MatrixSolutionState GetSolutionState(int? augmentedColCount = null);
public virtual Matrix Solve(int? augmentedColCount = null);
public virtual int GetRank(int? augmentedColCount = null);

Matrix Determinant

This function determinant uses the Laplace Expansion method. It works by calculating the cross-product of the matrix. Here’s the implementation:

/// <summary>
/// Calculates determinant. Internally uses Laplace Expansion method.
/// </summary>
/// <remarks>
/// Returns 1 for an empty matrix. 
/// See https://math.stackexchange.com/questions/1762537/what-is-the-determinant-of/1762542
/// </remarks>
public static double Determinant(double[,] input) {
  var results = CrossProduct(input);

  return results.Sum();
}

public static double[] CrossProduct(double[,] input) {
  int rowCount = input.GetLength(0);
  int colCount = input.GetLength(1);

  if (rowCount != colCount)
    throw new InvalidOperationException(Properties.Resources.Exception_RequiredSquareMatrix);

  if (rowCount == 0)
    return new double[] { 1 };

  if (rowCount == 1)
    return new double[] { input[0, 0] };

  if (rowCount == 2)
    return new double[] { (input[0, 0] * input[1, 1]) - (input[0, 1] * input[1, 0]) };

  double[] results = new double[colCount];

  for (int col = 0; col < colCount; col++) {
    // checkerboard pattern, even col  = 1, odd col = -1
    var checkerboardFactor = col % 2.0 == 0 ? 1 : -1;
    var coeffecient = input[0, col];

    var crossMatrix = GetCrossMatrix(input, 0, col);
    results[col] = checkerboardFactor * (coeffecient * Determinant(crossMatrix));
  }

  return results;
}

/// <summary>
/// Retrieves all matrix entries except the specified row and col. 
/// Used in cross product and determinant functions.
/// </summary>
public static double[,] GetCrossMatrix(double[,] input, int skipRow, int skipCol) {
  int rowCount = input.GetLength(0);
  int colCount = input.GetLength(1);

  var output = new double[rowCount - 1, colCount - 1];
  int outputRow = 0;

  for (int row = 0; row < rowCount; row++) {
    if (row == skipRow)
      continue;

    int outputCol = 0;

    for (int col = 0; col < colCount; col++) {
      if (col == skipCol)
        continue;

      output[outputRow, outputCol] = input[row, col];

      outputCol++;
    }
    outputRow++;
  }

  return output;
}

Matrix Inverses

The matrix inverse function eliminates a function and determines if all columns are unique by checking matrix rank. Another function checks if the matrix is invertible by checking determinant.

/// <summary>
/// Returns a value indicates whether the specified matrix is invertible. 
/// Internally uses array determinant.
/// </summary>
public static bool IsInvertible(double[,] input) {
  var rowCount = input.GetLength(0);
  var colCount = input.GetLength(1);

  if (rowCount != colCount)
    return false;

  return Determinant(input) != 0;
}

/// <summary>
/// Calculates the inverse of a matrix. Returns null if non-invertible.
/// </summary>
public static double[,] Invert(double[,] matrix) {
  var rowCount = matrix.GetLength(0);
  var colCount = matrix.GetLength(1);

  if (rowCount != colCount)
    throw new InvalidOperationException(Properties.Resources.Exception_RequiredSquareMatrix);

  var newMatrix = ConcatHorizontally(matrix, CreateIdentityMatrix(rowCount));

  var result = Eliminate(newMatrix, MatrixReductionForm.ReducedRowEchelonForm, rowCount);
  if (result.Rank != colCount)
    return null;

  return result.Solution;
}

Matrix Multiplication

Four variations of the Multiply function available: scalar multiplication, matrix multiplications, unsafe multiplications, and powers.

/// <summary>
/// Multiplies/Scales a matrix by a scalar input.
/// </summary>
public static double[,] Multiply(double scalar, double[,] input) {
  var rowCount = input.GetLength(0);
  var colCount = input.GetLength(1);

  // creating the final product matrix
  double[,] output = new double[rowCount, colCount];

  for (int row = 0; row < rowCount; row++) {
    for (int col = 0; col < colCount; col++) {
      output[row, col] = scalar * input[row, col];
    }
  }

  return output;
}

/// <summary>
/// Multiplies two matrices together.
/// </summary>
public static double[,] Multiply(double[,] matrix1, double[,] matrix2) {
  // caching matrix lengths for better performance
  var matrix1Rows = matrix1.GetLength(0);
  var matrix1Cols = matrix1.GetLength(1);
  var matrix2Rows = matrix2.GetLength(0);
  var matrix2Cols = matrix2.GetLength(1);

  // checking if product is defined
  if (matrix1Cols != matrix2Rows)
    throw new InvalidOperationException(Properties.Resources.Exception_UndefinedProduct);

  // creating the final product matrix
  double[,] output = new double[matrix1Rows, matrix2Cols];

  // looping through matrix 1 rows
  for (int matrix1_row = 0; matrix1_row < matrix1Rows; matrix1_row++) {
    // for each matrix 1 row, loop through matrix 2 columns
    for (int matrix2_col = 0; matrix2_col < matrix2Cols; matrix2_col++) {
      // loop through matrix 1 columns to calculate the dot product
      for (int matrix1_col = 0; matrix1_col < matrix1Cols; matrix1_col++) {
        output[matrix1_row, matrix2_col] += matrix1[matrix1_row, matrix1_col] * 
                                                matrix2[matrix1_col, matrix2_col];
      }
    }
  }

  return output;
}

/// <summary>
/// Multiplies two matrices together. Uses unsafe code. Better with extremely large matrices.
/// </summary>
public static double[,] MultiplyUnsafe(double[,] matrix1, double[,] matrix2) {
  // caching matrix lengths for better performance
  var matrix1Rows = matrix1.GetLength(0);
  var matrix1Cols = matrix1.GetLength(1);
  var matrix2Rows = matrix2.GetLength(0);
  var matrix2Cols = matrix2.GetLength(1);

  // checking if product is defined
  if (matrix1Cols != matrix2Rows)
    throw new InvalidOperationException(Properties.Resources.Exception_UndefinedProduct);

  // creating the final product matrix
  double[,] output = new double[matrix1Rows, matrix2Cols];

  unsafe
  {
    // fixing pointers to matrices
    fixed (
      double* pProduct = output,
      pMatrix1 = matrix1,
      pMatrix2 = matrix2) {

      int i = 0;
      // looping through matrix 1 rows
      for (int matrix1_row = 0; matrix1_row < matrix1Rows; matrix1_row++) {
        // for each matrix 1 row, loop through matrix 2 columns
        for (int matrix2_col = 0; matrix2_col < matrix2Cols; matrix2_col++) {
          // loop through matrix 1 columns to calculate the dot product
          for (int matrix1_col = 0; matrix1_col < matrix1Cols; matrix1_col++) {

            var val1 = *(pMatrix1 + (matrix1Rows * matrix1_row) + matrix1_col);
            var val2 = *(pMatrix2 + (matrix2Cols * matrix1_col) + matrix2_col);

            *(pProduct + i) += val1 * val2;
          }

          i++;
        }
      }
    }
  }

  return output;
}

/// <summary>
/// Raises an input matrix to the nth power.
/// </summary>
public static double[,] Power(double[,] input, int power) {
  if (input.GetLength(0) != input.GetLength(1))
    throw new InvalidOperationException(Properties.Resources.Exception_RequiredSquareMatrix);
  if (power < 0)
    throw new ArgumentException(nameof(power));
  if (power == 0)
    return CreateIdentityMatrix(input.GetLength(0));

  double[,] output = CreateCopy(input);
  for (int i = 0; i < power; i++) {
    output = Multiply(output, input);
  }

  return output;
}

Subspace Projection Matrices

The following function creates projection matrix from a subspace.

/// <summary>
/// Creates projection matrix for the specified subspace.
/// </summary>
public static double[,] CreateProjectionMatrix(double[,] subspace) {
  var subspaceTranspose = MatrixFunctions.Transpose(subspace);
  double[,] value = MatrixFunctions.Multiply(subspaceTranspose, subspace);
  value = MatrixFunctions.Invert(value);
  value = MatrixFunctions.Multiply(value, subspaceTranspose);
  value = MatrixFunctions.Multiply(subspace, value);
  return value;
}

Reflection Matrices

The following functions create 2D and 3D reflection matrices:

public static double[,] Create2DReflectionMatrix(MatrixAxis axis) {
  if (axis == MatrixAxis.Z)
    throw new InvalidOperationException(Properties.Resources.Exception_InvalidAxis);

  var output = CreateIdentityMatrix(2);

  if (axis == MatrixAxis.X)
    output[1, 1] *= -1;
  else  if (axis == MatrixAxis.Y )
    output[0, 0] *= -1;

  return output;
}

public static double[,] Create3DReflectionMatrix(Matrix3DReflectionPlane axis) {
  var output = CreateIdentityMatrix(4);

  if (axis == Matrix3DReflectionPlane.XY)
    output[2, 2] *= -1;

  else if (axis == Matrix3DReflectionPlane.YZ)
    output[0,0] *= -1;

  else if (axis == Matrix3DReflectionPlane.ZX)
    output[1,1] *= -1;

  return output;
}

Rotation Matrices

The following functions create 2D and 3D rotation matrices. They accept angle, unit (radians / degrees) and direction (clockwise / counter-clockwise):

/// <summary>
/// Creates 2-dimensional rotation matrix using the specified angle.
/// </summary>
public static double[,] Create2DRotationMatrix
       (double angle, AngleUnit unit, MatrixRotationDirection direction) {
  // sin and cos accept only radians

  double angleRadians = angle;
  if (unit == AngleUnit.Degrees)
    angleRadians = Converters.DegreesToRadians(angleRadians);

  double[,] output = new double[2, 2];

  output[0, 0] = Math.Cos(angleRadians);
  output[1, 0] = Math.Sin(angleRadians);
  output[0, 1] = Math.Sin(angleRadians);
  output[1, 1] = Math.Cos(angleRadians);

  if (direction == MatrixRotationDirection.Clockwise)
    output[1, 0] *= -1;
  else
    output[0, 1] *= -1;

  return output;
}

/// <summary>
/// Creates 2-dimensional rotation matrix using the specified angle and axis.
/// </summary>
public static double[,] Create3DRotationMatrix
     (double angle, AngleUnit unit, MatrixAxis axis) {
  // sin and cos accept only radians

  double angleRadians = angle;
  if (unit == AngleUnit.Degrees)
    angleRadians = Converters.DegreesToRadians(angleRadians);

  double[,] output = new double[3, 3];

  if (axis == MatrixAxis.X) {
    output[0, 0] = 1;
    output[1, 1] = Math.Cos(angleRadians);
    output[2, 1] = Math.Sin(angleRadians);
    output[1, 2] = -1 * Math.Sin(angleRadians);
    output[2, 2] = Math.Cos(angleRadians);
  } else if (axis == MatrixAxis.Y) {
    output[1, 1] = 1;
    output[0, 0] = Math.Cos(angleRadians);
    output[2, 0] = -1 * Math.Sin(angleRadians);
    output[0, 2] = Math.Sin(angleRadians);
    output[2, 2] = Math.Cos(angleRadians);
  } else if (axis == MatrixAxis.Z) {
    output[2, 2] = 1;
    output[0, 0] = Math.Cos(angleRadians);
    output[1, 0] = Math.Sin(angleRadians);
    output[0, 1] = -1 * Math.Sin(angleRadians);
    output[1, 1] = Math.Cos(angleRadians);
  }

  return output;
}

Shearing Matrices

The following functions create shearing matrices using a specific factor over the given axis.

public static double[,] Create2DShearingMatrix(double factor, MatrixAxis axis) {
  if (axis == MatrixAxis.Z)
    throw new InvalidOperationException(Properties.Resources.Exception_InvalidAxis);

  var output = CreateIdentityMatrix(2);

  if (axis ==  MatrixAxis.X)
    output[0, 1] = factor;

  else if (axis == MatrixAxis.Y )
    output[1, 0] = factor;

  return output;
}

public static double[,] Create3DShearingMatrix(double factor, MatrixAxis axis) {
  var output = CreateIdentityMatrix(4);

  if (axis == MatrixAxis.X) {
    output[1, 0] = factor;
    output[2, 0] = factor;
  } else if (axis == MatrixAxis.Y) {
    output[0, 1] = factor;
    output[2, 1] = factor;
  } else if (axis == MatrixAxis.Z) {
    output[0, 2] = factor;
    output[1, 2] = factor;
  }

  return output;
}

Vectors

The following lists some of the major vector functions covered in this library. We are having a look at the raw functions. Wrappers covered later.

Angels

This function calculates the angle between two vectors. It relies on two other functions, DotProduct and GetMagnitude.

public static double AngleBetween(double[] vector1, double[] vector2, AngleUnit unit) {
  if (vector1.Length != vector2.Length)
    throw new InvalidOperationException(Properties.Resources.Exception_DimensionsMismatch);

  var dotProduct = DotProduct(vector1, vector2);
  var lengthProduct = GetMagnitude(vector1) * GetMagnitude(vector2);

  var result = Math.Acos(dotProduct / lengthProduct);
  if (unit == AngleUnit.Degrees)
    result = Converters.RadiansToDegrees(result);

  return result;
}

Normalization

The following code demonstrates two operations: normalization (i.e., converting to unit vector) and magnitude (length) calculator.

/// <summary>
/// Normalizes a vector.
/// </summary>
public static double[] ToUnitVector(double[] input) {
  var length = input.Length;

  double[] output = new double[length];
  var coeffecient = 1.0 / GetMagnitude(input);

  for (int i = 0; i < length; i++) {
    output[i] = coeffecient * input[i];
  }

  return output;
}

public static double GetMagnitude(double[] input) {
  double val = 0;

  for (int i = 0; i < input.Length; i++)
    val += input[i] * input[i];

  val = Math.Sqrt(val);

  return val;
}

Dot-Product and Cross-Product

The following code demonstrates scaling, dot-product, and cross product.

public static double DotProduct(double[] vector1, double[] vector2) {
  if (vector1.Length != vector2.Length)
    throw new InvalidOperationException(Properties.Resources.Exception_DimensionsMismatch);

  double product = 0;
  for (int i = 0; i < vector1.Length; i++)
    product += vector1[i] * vector2[i];

  return product;
}

public static double[] Scale(double scalar, double[] vector) {
  double[] product = new double[vector.Length];

  for (int i = 0; i < vector.Length; i++) {
    product[i] = scalar * vector[i];
  }

  return product;
}

public static double[] CrossProduct(double[] vector1, double[] vector2) {
  int length = 3;

  if (length != vector1.Length || length != vector2.Length)
    throw new InvalidOperationException(Properties.Resources.Exception_3DRequired);

  double[,] matrix = new double[length, length];
  for (int row = 0; row < length; row++) {
    for (int col = 0; col < length; col++) {
      if (row == 0)
        matrix[row, col] = 1;
      else if (row == 1)
        matrix[row, col] = vector1[col];
      else if (row == 2)
        matrix[row, col] = vector2[col];
    }
  }

  return MatrixFunctions.CrossProduct(matrix);
}

Projection

Projection of a vector onto another vector is handled using the following functions:

public static double ProjectionFactor(double[] vector1, double[] vector2) {
  return DotProduct(vector1, vector2) / DotProduct(vector2, vector2);
}
public static double[] Projection(double[] vector1, double[] vector2) {
  var factor = ProjectionFactor(vector1, vector2);
  return Scale(factor, vector2);
}

Wrappers

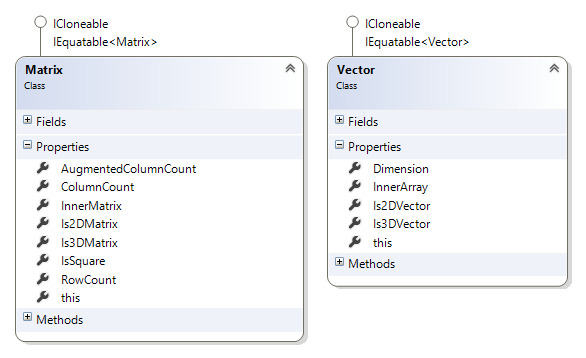
Working with raw Array objects especially multi-dimensional arrays is fairly cumbersome. To make it easier, we wrapped those raw functions into two wrapper classes, Matrix and Vector. Both classes implement ICloneable and IEquatable. Both have indexers and a direct way to access their inner representation (i.e., array).

Properties and Methods

The following figures show the exported members of both classes.

Operators

We overrode some operators for both classes to allow clean and clear access to their operations. Here’s the overridden operator list for Matrix:

public static Matrix operator +(Matrix m) { return m; }
public static Matrix operator -(Matrix m) { return m.Scale(-1); }
public static Matrix operator +(Matrix a, Matrix b) { return a.Add(b); }
public static Matrix operator -(Matrix a, Matrix b) { return a.Subtract(b); }
public static Matrix operator +(Matrix a, double[,] b) { return a.Add(b); }
public static Matrix operator -(Matrix a, double[,] b) { return a.Subtract(b); }
public static Matrix operator *(double a, Matrix m) { return m.Scale(a); }
public static Matrix operator *(Matrix a, Matrix b) { return a.Multiply(b); }
public static Matrix operator *(Matrix a, double[,] b) { return a.Multiply(b); }
public static bool operator ==(Matrix a, Matrix b) {
  if ((a as object) == null || (b as object) == null)
    return false;
  return a.Equals(b);
}
public static bool operator !=(Matrix a, Matrix b) {
  if ((a as object) == null || (b as object) == null)
    return false;
  return a.Equals(b) == false;
}
public static Matrix operator ^(Matrix a, int power) { return a.Power(power); }
public static implicit operator double[,] (Matrix m) { return m.InnerMatrix; }
public static explicit operator Matrix(double[,] m) { return new Linears.Matrix(m); }

Last Word

As stated previously, the code is using the MIT license. So please use the code without any restrictions, limitations, or warranties, and feel free to relay your comments, suggestions, and corrections.

History

• 12^th March, 2020: Initial version