How to write the fastest possible Chess Position code. What tricks are used - what ideas are implemented. Many optimizations are applicable to other high performance code. Familiarity with allowed chess moves required. Given any Chess position - count all chess positions following that move in the least amount of time.
Github source - https://github.com/Gigantua/Gigantua
If you like this Article - lets drink a coffee together! https://www.buymeacoffee.com/Pontifex
Run with: giga_win "r3k2r/p1ppqpb1/bn2pnp1/3PN3/1p2P3/2N2Q1p/PPPBBPPP/R3K2R w KQkq" 6
This movegenerator can generate 2 billion chessmoves per thread and per second!
Introduction
Quote:
Chess is a beautiful programming challenge. A chessboard has exactly 64 squares which do fit perfectly into a single 64-bit register.
This brings us to really exciting algorithmic ideas that operate on a few register to enumerate all chess moves. For example loops or branches are not needed to walk all 8 pawns forward:
All empty squares can be expresses as: ~(White | Black)
All 8 white pawns marching forward can be expressed as: (WPawns << 8) & Empty

(Enpassant capture with check)
Any Chess position consists of 18 distinct elements. 12 types of pieces - queen, rook, bishop, knight, king, pawn for each color.
Current Moving Color - 1 Enpassant pawn - 4 Castling squares - left/right per color
Quote:
The fastest possible piece of code you can ever write is non existing code. It runs in 0 time and has no overhead. Template metaprogramming and constexpr evaluation in C++ give us these tools.
Writing fast code in any programming language means:
- moving as much work as possible into compiletime
- replacing branches by branchless programming
- inserting domain knowledge into the code
For example, after pushing a pawn from the first Rank - an Enpassant Pawn is created. It can be captured in a special way by another pawn. But only for one single move. Every State that exists in only a handful of positions out of Billions should not even need an if statement. Compilers and Cpus do a good job of hiding branch latency - yet by replacing an if else chain by branchless bitwise arithmetic - an order of magnitude, faster code can be achieved. The cost is there but it is hidden most of the time.
The Problem
How many moves are in this position after 3 moves by each player?
How many checks - how many checkmates?
A movegenerator can answer these questions very fast.
Time taken: 85ms
Moves: 119060324 Checks: 809099 Checkmates: 10828
That is 119 Million in 85ms or just about 1400 Million nodes per second. (I will count a move as a node)
Chess is an exponential expanding tree with a branching factor of ~25. Where if building an engine aggressive pruning methods need to happen to see good and appropriate moves 20 plys deep. Asking the possible move count question for depth 7 - will take 2100ms. This movegenerator is just that. A very fast piece of code to expand any position into all possible answers. This is one core piece of any chess engine.
The Bitboard
We define a canonical Chess Bitboard: map = uint64_t
Which means that the white pawns are: 0b1111111100000000
The black pawns are 0b1111111100000000 << 40
It is clear that the space efficiency for the king is not very good since it's only a single bit out of 64. But Bitboards also means that moving can be done very efficiently by just shifting the king around. Moving the king up and left on the board is literally only King <<= 9. Moves can be done in shifts. Forbidden moves can be pruned with &~.
That is the beauty of the bitboard approach. It takes one instruction to remove forbidden moves no matter how many there are.
struct Board {
const map BPawn; const map BKnight; const map BBishop; const map BRook;
const map BQueen; const map BKing;
const map WPawn; const map WKnight; map WBishop; const map WRook;
const map WQueen; const map WKing;
const map Black;
const map White;
const map Occ;
constexpr Board(
map bp, map bn, map bb, map br, map bq, map bk,
map wp, map wn, map wb, map wr, map wq, map wk) :
BPawn(bp), BKnight(bn), BBishop(bb), BRook(br), BQueen(bq), BKing(bk),
WPawn(wp), WKnight(wn), WBishop(wb), WRook(wr), WQueen(wq), WKing(wk),
Black(bp | bn | bb | br | bq | bk),
White(wp | wn | wb | wr | wq | wk),
Occ(Black | White)
{
}
}
The choice here is an expanded bitboard and non obvious. For example one we could only have fields for 6 pieces and White - Black separately. Then a Black Pawn = Black & Pawn. But we go for speed and that means every visited game node needs about 18 instructions less. Even more compressed are 4x 64 bit integers where each piece is compressed as the binary table of that 4 squares for that piece. 0000 = Empty, 0001 = Black pawn, etc.
Since we need all pieces for each move, we need an expanded bitboard.
Notice how the current moving color or castling rights are not a part of this definition. It is part of the gamestate.
Solving Bitboard Chess
The relevant chess rules are as follows: You must not be in check at the end of your turn. Check is when an enemy piece sees your king. While in check, you cannot castle. An Enpassant move exists if your enemy pushed a pawn forwards 2 squares. A piece can move if it would not result in a check, and the target square is an enemy or empty.
So for the insane performance we aim for - our goal is to have a legal movegenerator. (Older approaches check for king safety later and undo the move after they already made it which is too expensive). In fact our approach does not need any movelist at all - more to that in the chapter visitor pattern.
A legal move is any move that moves a piece to any allowed square while our own king cannot be taken in the next move by the enemy. (exception to that rule is castling - where the king cannot pass through attacked squares)
Notice how that idea goes very well with bitboards and fits into a single register in a single operation.
This is a compiletime function which will get inlined into the membername of the board (depending on the current moving color) - and is the basis for a legal move: EnemyorEmpty is all 64 squares which a piece can move to:
template<bool IsWhite>
_Compiletime map EnemyOrEmpty(const Board& brd)
{
if constexpr (IsWhite) return ~brd.White;
return ~brd.Black;
}
Now thats the easy part - we have lookup functions for all 6 pieces. Kings and Knights can be looked up directly. Pawns are fastest to shift up and prune all blocked pawns. (Its best to read the sourcecode for those)
Sliding pieces need a special lookup table which is described in chapter "Fast Piece Lookup".
These together would already yield all pseudo legal bits in a handful of instructions and with zero branching!
map pseudomoves = Lookup[knightsquare] & EnemyOrEmpty<white>(brd)
To go from pseudolegal moves to full legality without ifs I tried a lot of different things - and one day I had the idea hot to prune all moves for checks and pins also. Expanding on the above idea we can prune the pseudomoves by the checking legality and pin legality to obtain a perfect movegenerator:
1) We Define a checkmask
You will see why it's done later:
It is all bits set to 1 - except when there is a check on our king. Then it is the path from the enemy to the king:
Now what the hell is going on? - It's very simple. Defining the Checkmask as the path from the enemy to the king - sliders get multiple bits - and knight and pawns get themselves added to the checkmask. Or all bits set when there is no check allows the simplest of move pruning.
Just logical & ANY move with the checkmask. You will get the allowed moves.
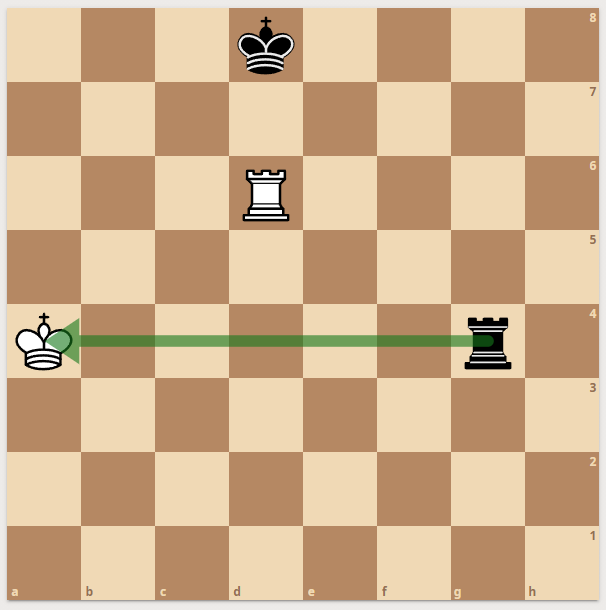
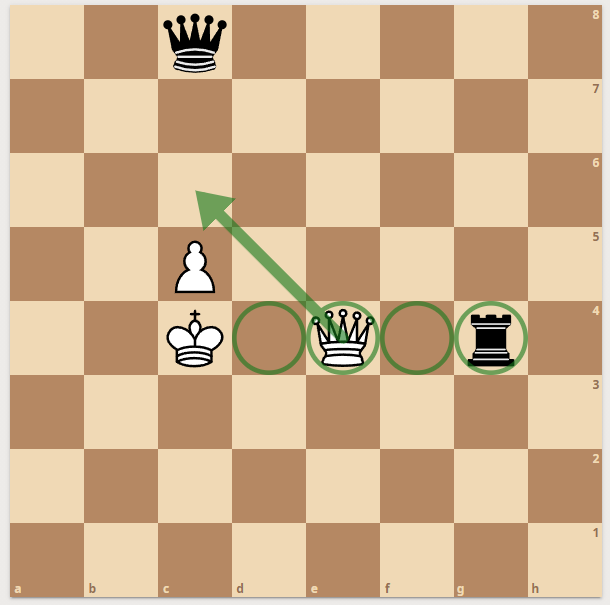
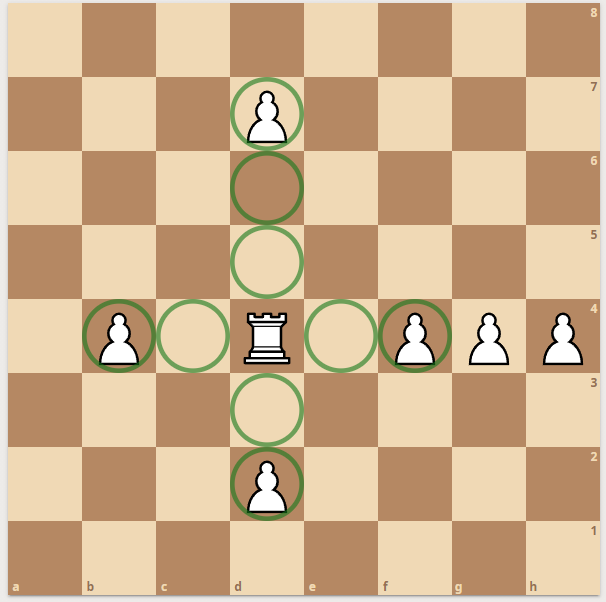
Now here is an example - white king is checked by black rook:
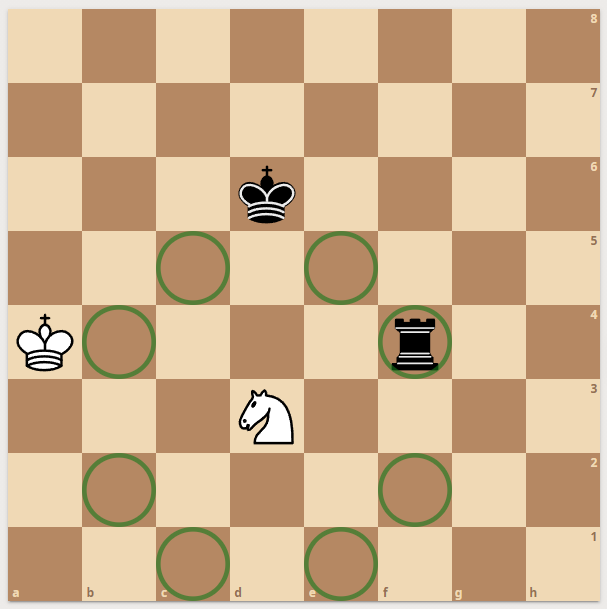 | 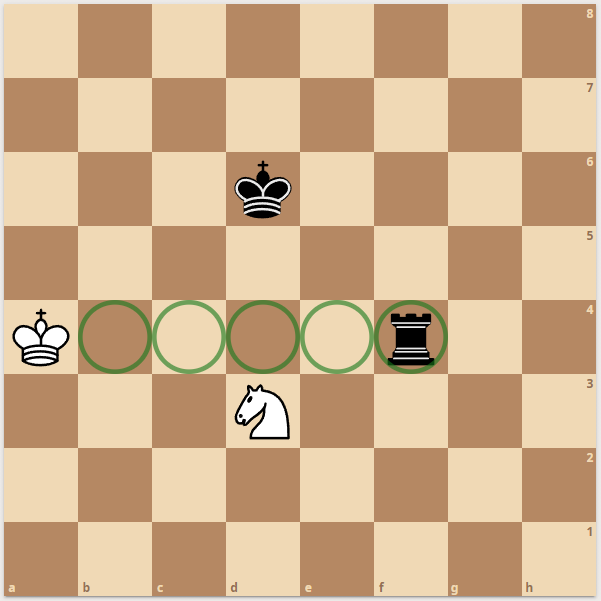 | 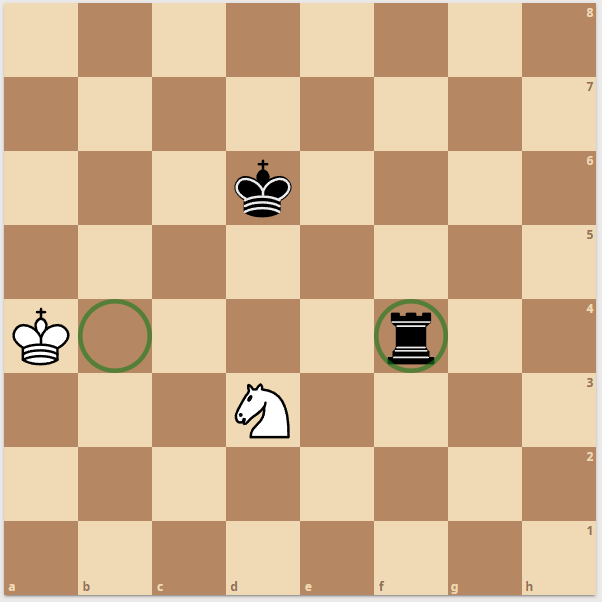 |
| Knight moves
| checkmask
| move & checkmask
|
Now. If there are two checks - we don't even get to enumerate knight moves. Since one piece cannot take two pieces at once - the only possible moves are the moves by the king. For the king during double check - all moves are possible when the target square is an Enemy or Empty + The square is not seen by an enemy.
Defining the checkmask this way solves many many unpleasant problems automatically. But it's not enough:
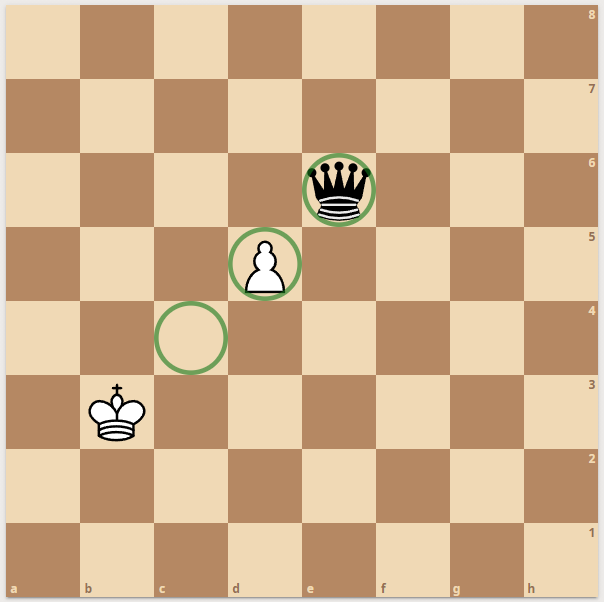
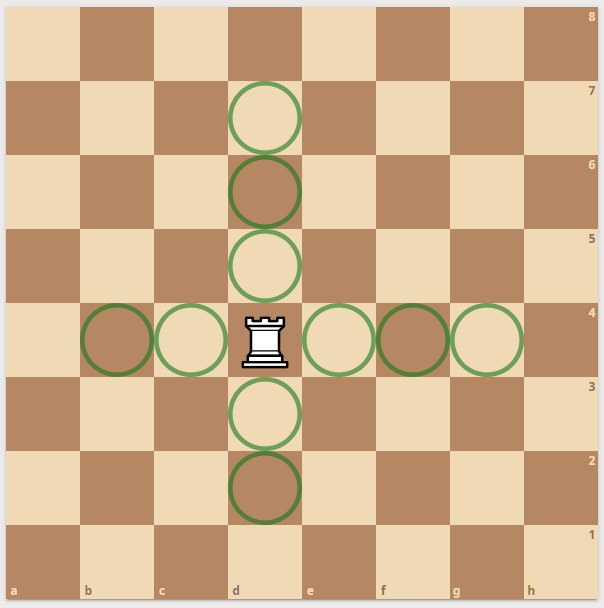
2) We Define a pinmask
Sometimes, moves are possible - but still forbidden since an enemy hides behind your own piece and is eyeing the king. This is called xray.
 |  | 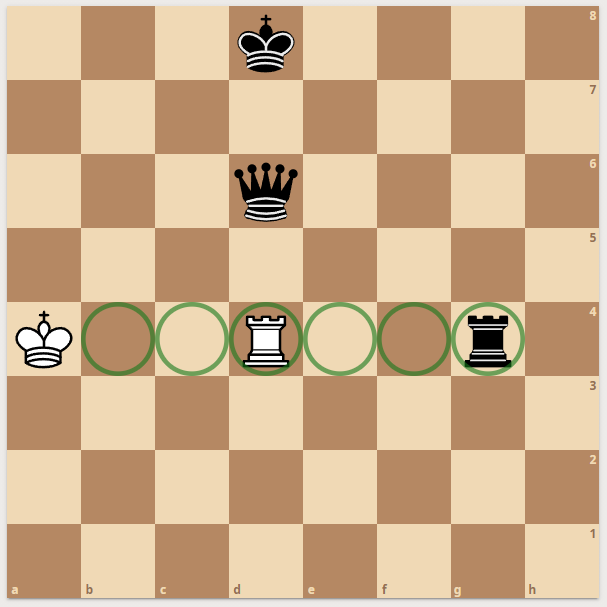 |
| Rook eyeing the king
| Forbidden Rook move
| Definition of pinmask
|
Pins are much harder to get right. We can have one check per move. But we can have up to 8 pins. A king can be surrounded by pieces that all are pinned. The pinmask is the path from the enemy to the king if our own blocking piece were removed. This can also be done in a single lookup (sliding pieces explained below) - where the xray lookup table just contains the mask as defined on the rightmost image above.
Now the beauty of defining the pinmask like this has these advantages:
a) Only pinned pieces have less moves to play than possible - The pinned piece is a member of the mask
We have two define two directions (you will see why - in point b)
HorizontalVertical = HV, Diagonals = D12
Now with Bitboards it becomes really easy to get all pieces that can move - and loop over those only:
To get all pinned Rooks for example: Rooks & pinHV
To get all Knights that can move (a pinned knight can never move): Knights & ~(pinHV | pinD12)
To get all Knight moves (for 1 knight) generally:
Lookup[knightsquare] & EnemyOrEmpty & checkmask & ~(pinHV | pinD12)
That is the beauty of this approach - is that there is not a single if condition here. All knight moves get looked up and pruned in only a few instructions without a single condition. These are all allowed target squares that maybe prevent check and also check if the knight is not pinned. The output is a single 64 bit integer which is the bitmask for the allowed moves.
Normal movegens would have at least one lookup and 8 ifs in a loop to check if the move is possible. Or even slower - do the move and check if the king is in check for every move. The pin + checkmask will prune towards legality of any move perfectly!
b) Pinned pieces can still move along the axis they are pinned on.
What I didn't tell you is that we need to have pins defined along both diagonals. Since a pin can exist from a rook or a bishop or a queen - the pinned piece is still forbidden to go to the other pinmask:
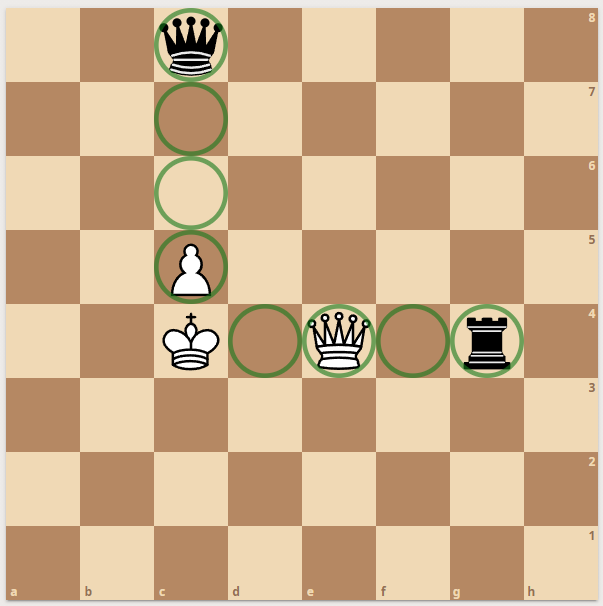 |  |  |
| Naive pinmaks
| Pins Split by HV - D12
| A pinned pawn
|
A pawn can move like a queen - HV or D12. So it also is handled like a queen. In principle, it also can be pinned along a specific axis and can only move along that axis anymore.
So the pinned pawn on the right cannot move forward. Since it's a member of the
- A pinned knight cannot move
- A HV pinned rook can only move along HV - it cannot see V from H and the other way around
- A D12 pinned rook cannot move
- Same for queen, bishops and pawns
3) Bringing It Together
All types of check are handled by the checkmask.
All types of pins are handled by selecting the members of that pin: Rooks & PinHV - for pinned rooks, the move is:
SeenSquaresByRook & EnemyOrEmpty & checkmask & PinHV
All types of unpinned pieces are handled by selecting: Rooks & ~PinHV - for them, the move is:
SeenSquaresByRook & EnemyOrEmpty & checkmask
For pawns, we have to select pawns that can attack right diagonally (enemy is there) and are not HV pinned.
(Pawns & NotRightFile << 7) & (~PinHV | Enemy >> 9)
This gives us 0...8 set bits in a 64 bit bitmask that correspond to the white pawns that have an enemy on their right side and are not pinned. The important part is that there is no if statement - only the if of the for loop condition - which doesn't even need a seperate variable for counting! This can be seen below.
You can read every detail in the code but the idea is the same. You only need a handful of loops and & with checkmask and pinmask to prune every semilegal move to total legality.
4) Summary
For all types of pieces, we get the legal moves from above algorithm. But there are two issues - king moves - castling and enpassant. Enpassant is easiest to lookup in the code but the trick is to have it constexpr compiled away when the last move didn't push a pawn from first rank to 3rd rank (very rare). The legality check of enpassant can be tricky in normal code - but we have the pinmask already so we perfectly know if an enpassant is illegal like that position:
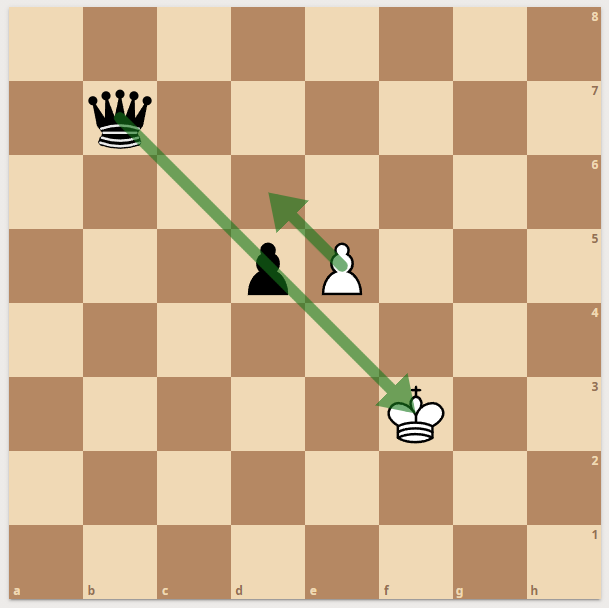 |  | 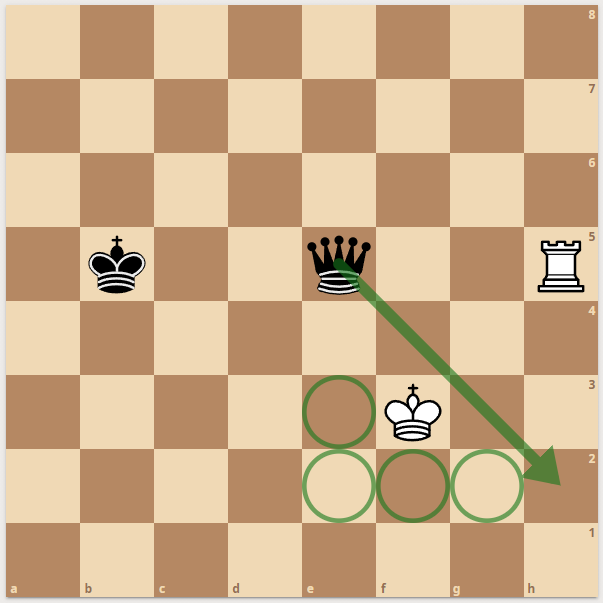 |
| pinned Enpassant
| Castling squares
| Pinned Queen prevents king
|
For pinned Enpassant, we just check if the pawn we will take would be a member of a pin. This is almost free.
For castling. we have to know if the squares the king is passing through are attacked. Also, all king moves are different from all other moves - a king cannot move to a seen square. (Enemy Pawn - Knight - Bishop, etc. can see that square. If they are pinned is irrelevant as can be seen on the right side. The Queen is pinned but the king can only move to the green squares.
I tried a long time to write code to just remember which squares are attacked by an enemy piece - but you would have to remember how often a square is attacked and on piece move, update that table - If you think about it - you would lookup into a 64 square table. Which you already are for the king - and knights. Pawns are free. The only costly "seen by" operations are the sliders - but they don't cost much too.
It's fastest to just loop over the enemy sliders but remember what the enemy knights and pawns can see. That only needs two uint64_t variables.
So we can say that there are 4 levels for any piece in chess that generate the legal moves:
- Seen Squares
- Movable Squares
- Checked Squares
- Pinned Squares
Seen Squares - For Kingmove and Castling - only seen by Enemy matters. The king cannot move to squares that are seen by enemies. No matter the pins, etc. In fact, this engine doesn't even calculate for castling or seensquares if the king is blocked in by own pieces + enemy knight + enemy king. That runtime-check is almost free.
Movable Squares - A lookup operation for the Lookup<PieceType>(position, occupy) & EnemyOrEmpty. These are the squares a piece can walk/jump to. For King and Knight, it's a simple lookup. For pawns, it's a lot of shift operations - in all directions + Enpassant. For Sliding pieces, it's a lookup with the occupy board in a table. It's the fastest way by far and explained below.
Checked Squares - Squares that would prevent the currently active check. Includes taking the enemy - or blocking all squares in the path.
Pinned Squares - If a piece is a member of a pinmask - it can only move among the members of that mask. So if Rook & PinHV => moves &= PinHV.
Legal Square - Just logical & of all above Squares and you end up with 100% legality. Not more not less. All for the cost of 4 instructions. I experimented a lot with remembering pins from last move, etc. but all tries just added a lot of code and became slower. Incremental Pins are possible by just refreshing the pins if something in the xray of the king changes.
Moving gamestate from runtime into compiletime
Why waste computer cycles and memory space if C++ can constexpr if away the enpassant pawn. The same holds true for the castling squares and most importantly the current moving color becomes a compiletime template and not an if statement. No single if statement should be wasted on non existing moves or which colors move it currently is.
These fields shall exist outside of the runtime. They exist during compiletime and are switched and replaced like a state machine.
class BoardStatus {
public:
const bool WhiteMove; const bool HasEPPawn;
const bool WCastleL; const bool WCastleR;
const bool BCastleL; const bool BCastleR;
constexpr BoardStatus(bool white, bool ep, bool wcast_left,
bool wcast_right, bool bcast_left, bool bcast_right) :
WhiteMove(white), HasEPPawn(ep), WCastleL(wcast_left),
WCastleR(wcast_right), BCastleL(bcast_left), BCastleR(bcast_right)
{
}
}
Not all board state can become a template. Only booleans (or very limited ranges) and every boolean added will double the cost in terms of code size. Also, they have to be completely independent - but these fields 6 are for chess. This will correspond to 64 functions the template will instantiate. That's the price of performance.
Now we only need a switch statement as an entry point into our recursive countmove function. But we already did very much. We have 6 independent boolean board state flags - and none of these will ever need a single if during runtime. The cost of having if (Color == White) or Attack[Color] compiles away into nothingness. We only need a single switch statement as an entry point.
Now we have a runtime entrypoint for our compiletime Template. But what if a piece moves - how can C++ transfrom an existing Template into something else?
constexpr BoardStatus SilentMove() const {
return BoardStatus(!WhiteMove, false, WCastleL, WCastleR, BCastleL, BCastleR);
}
template<class BoardStatus status>
MoveFunc(Move& move, Board& board){
MakeMove<status.SilentMove()>(move, board);
}
Simple. A constexpr member function inside the compiletime template class is also a compiletime constant. It's like White -> !White in a template but for all the other flags too. Most moves only affect the color flag - but moves like king or rook moves affect the castling flags. When the right rook moves, the appropriate right castling flag is removed (as a constexpr method that is called inside an if when castling was availible but the rook moved).
The same goes for the Enpassant pawn. When a pawn is pushed, we set the flag. The specific square of the pawn gets stored in runtime memory - Simple as that.
The Visitor Pattern
Now we are going for maximum performance. Most movegenerators use a function that will put all moves into a list like that:
Approach 1 - The movelist:
*move++ = MakeMove(from, to, state)...
Some define an iterator that will look like this:
Approach 2 - The iterator class:
for(auto move : getmoves(position)){
brd = Makemove(move);
EnumerateMoves(brd);
brd = Unmakemove(move);
}
But there is faster way! - A listfree compiletime inlineable function callback. By having our decision code not inside any loop body at all. The instant we find a valid move, we have a "callback" that decides what to do with it. Putting it into a list? Totally possible inside the callback, but not mandatory. Having a big block of memory filled for all ~30 moves on average is a huge cost for the movegenerator. Move sorting can still occur for an engine project by having 8 slots for the best moves. That's a lot cheaper.
That's the real cost of make/unmaking a move. You visit each move 2x. First, when you decide if its legal. And then a second time when you enumerate it. This visitor pattern totally negates that cost.
For example, this code resolves all checks - enumerates all moves and if double check - only enumerates the kings moves. I have removed some code to make it clearer and we focus on the kingmoves:
template<class BoardStatus status, class Callback_Move, int depth>
_NoInline void EnumerateMoves(Board& brd) {
map checkmask = Movestack::Check_Status[depth];
map kingban = Movestack::Atk_King[depth - 1] = Movestack::Atk_EKing[depth];
map kingatk = Refresh<status, depth>(brd, kingban, checkmask);
if (checkmask == 0xffffffffffffffffull) {
_enumerate<status, false, Callback_Move, depth, false>
(brd, kingatk, kingban, checkmask);
}
else if (checkmask != 0) { _enumerate<status, false, Callback_Move, depth, true>
(brd, kingatk, kingban, checkmask);
}
else { Bitloop(kingatk)
{
const Square sq = SquareOf(kingatk);
Movestack::Atk_EKing[depth - 1] = Lookup::King(sq);
Callback_Move::template Kingmove<status, depth>
(brd, King<status.WhiteMove>(brd), 1ull << sq);
}
}
}
The interesting part here is the Callback_Move::template Kingmove part that in turn calls the method which we enumerated from the class MoveReciever. You see we pass the type of a class in there that matches the template inside the enumerator code. This way, we can have the movegenerator inline any code we want into itself. We don't pay the cost of enumerating each move twice. The instant we detect a possible move - we have the appropriate code decide what to do with it.
That way, we know that the king moved on this depth with that status and from/to. Please note in this code that status.KingMove() is a compiletime template that will call the appropriate function where castling is not possible anymore. After the king moves - not even a single operation is wasted on checking for castling rights.
class MoveReciever
{
public:
template<class BoardStatus status>
static _ForceInline void PerfT1(Board& brd)
{
nodes += Movelist::count<status>(brd);
}
template<class BoardStatus status, int depth>
static _ForceInline void PerfT(Board& brd)
{
Movelist::EnumerateMoves<status, MoveReciever, depth>(brd);
}
template<class BoardStatus status, int depth>
static _Inline void Kingmove(const Board& brd, uint64_t from,
uint64_t to) {
Board next = Board::Move<BoardPiece::King, status.WhiteMove>
(brd, from, to, to & Enemy<status.WhiteMove>(brd));
if constexpr (depth == 2) {
PerfT1<status.KingMove()>(brd);
}
else PerfT<status.KingMove(), depth - 1>(brd);
}
}
Of course, there are also functions for KingCastle Pawnmove, PawnEnpassantTake, Pawnpush, Pawnpromote, Knightmove, Bishopmove, Rookmove, Queenmove. These all look similar to the above king and only differ if they need a status change and the board move. For example, the movegenerator knows if a piece was taken and thus the Board::Move code is a lot simpler.
Now you can see the power of the visitor pattern. Your own code is not a function pointer callback - but a compiletime inlinable piece of code that totally negates any need for iterating over all moves. Counting how many castles, kingmoves, knightmoves, etc. is almost free by just adding a castlingcount++ into the appropriate function. This will get inlined into movegen itself!
Why Is It So Fast? Summary
Efficient branchless pins and checks go a long way - but it wouldn't be enough to generate the fastest movegenerator of all. The heavy usage of constexpr castling and enpassant handling brings another 3x improvement. When castling is not possible, there is no condition in the assembly anymore. The template instantiation + if constexpr totally removes the cost of castling and enpassant. The shift direction of Pawn is also dependent on the color - which gets compiled to >> 8 vs << 8. But there is no lookup like shift[color] or condition the code is instantiated correctly.
The last improvement was the listless recursion. The instant a move is possible, it can get analyzed and expanded - stored - or not. Your choice. This "callback interaface" also provides nice eight methods that are named after the piece that is moving and contains all the relevant information right then and there.
Removing as many if statements as possible, I found out that a single if is a valid tool to make code faster - but only if the code inside it has 20+ instructions. Modern processors do a lot of things to hide the penalty of a branch - but it is still there. Having totally branchless code makes you feel the impact of every removed statement.
It was very fun optimizing this code - ever if statment removed added 30 Million nps to the generator. Every single logical AND statement (of which the impact is normally hard to measure) added around 2Mnps.
At the time of this writing, the movegenerator is on average 8x faster than the leading movegen written in C and generates 2 billion possible legal moves per Core and per Second!
Enumerating Moves
This is of interest since this is a bitboard movegenerator: Enumerating the bits in a uint64_t means enumerating all set bits in terms of their set bits in the fastest possible way.
#define SquareOf(X) _tzcnt_u64(X)
#define Bitloop(X) for(;X; X = _blsr_u64(X))
map bishops = BishopQueen<enemy>(brd);
Bitloop(bishops) {
const Square sq = SquareOf(bishops);
map atk = Lookup::Bishop(sq, brd.Occ);
}
The fastest code for that is the template on line 2 which evaluates the register for 0 - and then while it's not zero pops the least significant set bit. This for loop is zero check loop in itself so if no bishops are on the board - the loop is not entered at all!
Reset Lowest Set Bit or _blsr is equal to this: (src-1) & src but as an intrsinsic operation.
Getting the Square of the bit is really easy: The Trailing Zero Count (_tzcnt_u64) of the 64bit register is equal to the square. It's not off by 1 - it's just perfect!
Fast Piece Lookup
There are many approaches that would warrant their own article and are interesting in their own right. They have interesting mathematical properties like like perfect hashing.
I will focus on the root problem for sliders.
Knights - King are solved by a single lookup into a 64 square table:
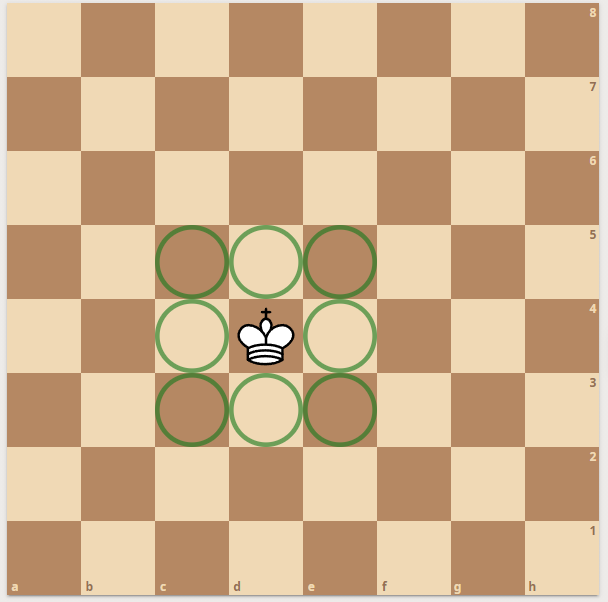
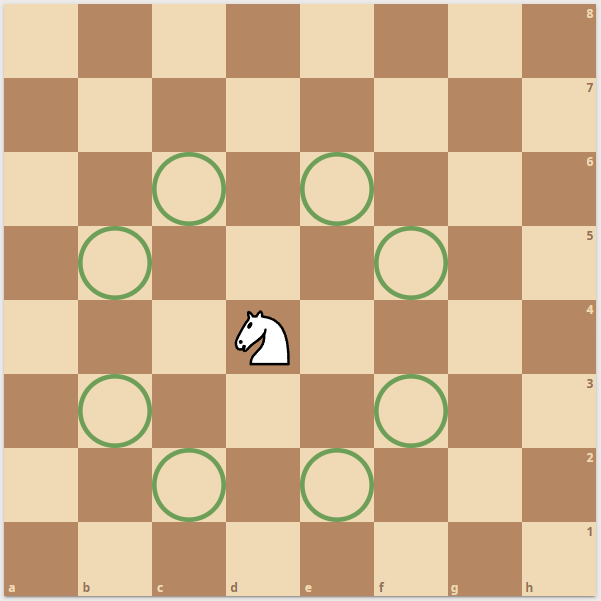
Pawns are fastest by directly shifting all pawns and having the code resolve all pawns that can attack left, right, and move forward. There are algorithms that can solve all knights at the same time - by a true bitboard approach. But that is not a real solution since we always need to know which source square we depart from.
The movegenerator must know which piece to move. It's not enought to say: All knights can go to these squares.
 |  |
| Attacked Squares
| Relevant Bits
|
Imagine if the relevant bits are transformed somehow into a sequence of bits at the lowest possible position. So for any occupation or blocking of the rooks path - we get all bits sequentially: 0b(45 zeros) 001001110101110.
That would make it possible to directly look up the attacked squares from the occupation. We cannot do that for the queen directly because there are too many relevant bits. But queen = RookAtk | BishopAtk is the same work. Luckily, we don't have to do much work at all since modern x64 processors have a specific instruction for that:
_pext_u64. Given any mask, it will gather these bits in the mask and put them into ascending order in the lsb.
Doing that manually would take a loop with two variables at least to check every bit sequentially and set them in ascending order.
Modern processors (Ryzen 5000+ / Intel) do that with a latency of 2 and throughput of 1. Meaning it's a very cheap instruction on the silicon level.
This is perfect for us - we only need to fill a lookup table. And have a smaller lookup for 64 masks of the relevant bits for each and every square on the board. Rook an Bishop.
The code looks like this:
return AttackPtr[_pext_u64(blocker, Mask)];
Mask and AttackPtr need to be looked up per square - but it's very cheap in general and does not contain a single if statement to test bits in a loop for each direction (like it's normally done).
Optimisations
What I didn't mention in the article - is that the King cannot move backwards when it's seen by an enemy rook. We just define the pinmask to contain the square behind the king. The pinners cannot jump over the king and we can use the same table for different operations. I also omitted all the masking away of border squares which unfortunately is needed for pawns - since a pawn on the left cannot go left anymore. It is a single & instruction but it is needed.
Pinned Queens move like a pinned Rook or a pinned Bishop. It's much faster to add them to the same enumerating loop instead of having 3 loops for the queen.
I relied heavily on the compiler to do the right thing. But some tricks are still necessary. For example, the checkmask normally prunes every move with &. Which is a very cheap instruction. But we want more speed! If the compiler knows that all bits are set (i.e., no check on the board), it will remove the & operation for us. This can be done inside the method in an if statement but that would need multiple ifs around the code. So adding a <bool inCheck>(map checkmask) parameter and having the compiler use the checkmask or if the template is true using 0xFFFFF.... as the mask made the code a lot faster.
To make that clear: a single if statement for a template parameter will remove every & pruning for every move in the current position (~ 30), this gave a nice boost of 200Meganodes/s.
One easy optimisation was bulk counting for leaf nodes. Since we enumerate all moves - it is not needed to expand the position in actuality on depth == 1. A simple Popcnt instruction will be enough. This needs to be disabled for an actual engine.
I tested different compilers and CLANG and MSVC are on the very top. Clang emits a little faster code - but MSVC compiles much faster. Just make sure to omit the frame pointer. That adds 5% of speed.
Compiler flags for CLANG:
-march=native -std=c++20 -lstdc++ -O3 Gigantua.cpp -flto -o giga_clang
This was a lot of fun. When the movegenerator was so fast (2 Billion nps), every single instruction that was taken away was measurable. I set the core to fixed 4.5ghz. Every removed if statement added around 30Mnps so that a profiler was not needed at all to measure improvement.
Interesting Positions
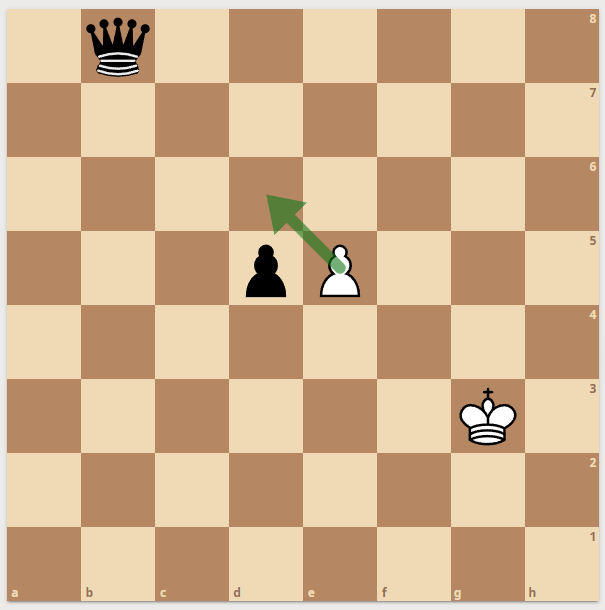
These positions are interesting for me because they uncoverer flaws in many movegenerators.
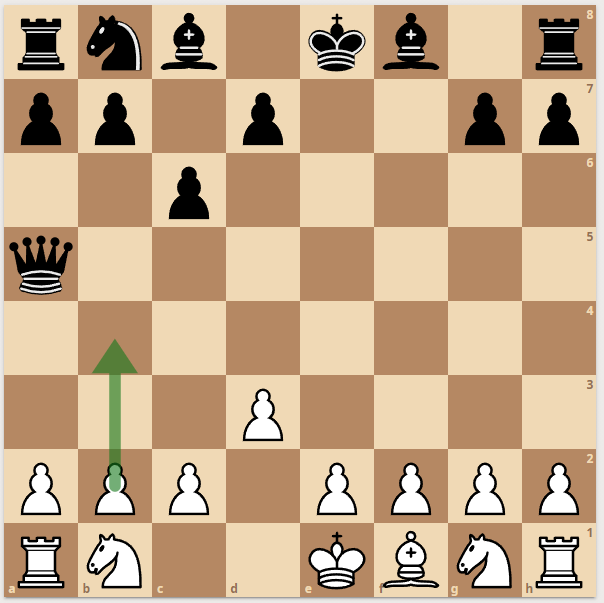
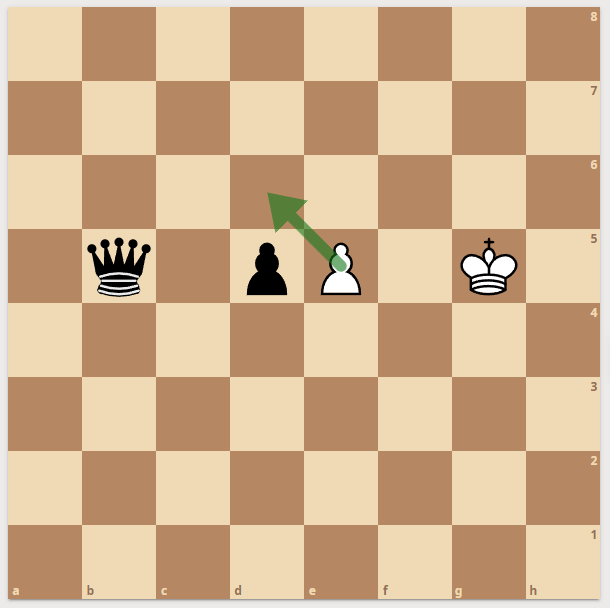
Left) You cannot generalize from a moveable pawn to a pushable pawn. Since there are positions where you cannot move - but only push.
Middle) The Enpassant taking white pawn is pinned along a diagonal but can take to the left and this is legal! - This is completely covered by my approach and does not need special handling. When the other diagonal is also pinned, the move gets pruned away by one logical &.
Right) This position will always need special care! - The only move where two pieces can vanish on a single rank is enpassant. This is the only move that needs extra code in my movegenerator! - Removing both blockers and checking if an enemy rook or queen can see the king.
if constexpr(HasEP) if (EPRank & King&& EPRank & EnemyRookQueen)
Check if legal - so it's almost free too!
If you enjoyed this article like I did writing -
please leave a comment below! - or consider buying me a coffee! - https://www.buymeacoffee.com/Pontifex
History
- 6th October, 2021: Initial version
