Introduction
This article provides a basic introduction to neural networks and neural network programming using the Encog Artificial Intelligence Framework. Encog is an AI framework that is available for both Java and Microsoft .NET. In this article, I will show you how to create and train a very basic neural network with Encog for C#. I will likely follow this up with more complex neural network examples in the future. However, for now, this article shows you how to get started with Encog.
There is a similar article that shows how to do this same thing for Java. You can find it here at The Code Project, as well.
Background
Encog is an advanced Artificial Intelligence Framework. Using Encog, you can create advanced neural network applications. Though Encog supports other aspects of Artificial Intelligence programming, this article will focus on neural network programming. Neural Network programming is the primary focus of Encog, as of version 2.3. Encog is released under the Lesser GNU Public License (LGPL). Encog can be downloaded from the following URL: http://www.heatonresearch.com/encog/.
This is a simple introductory example that shows how to create a neural network that recognizes the XOR operator. The XOR operator is essentially the "Hello World" of the neural network world. It is often used to demonstrate a new neural network.
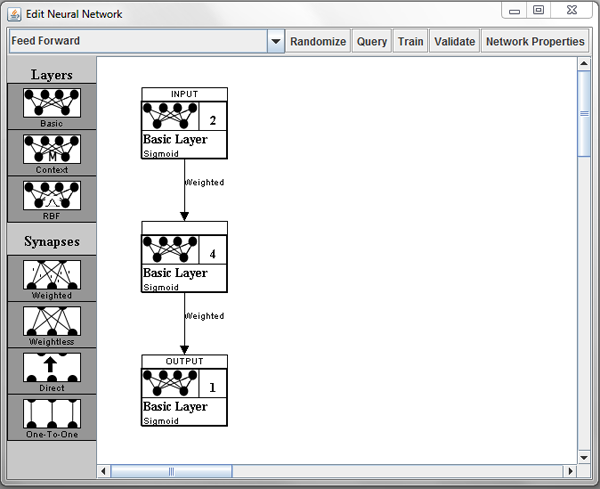
Before I show you how to create a neural network in Encog, it is important to understand how a neural network works. Nearly all neural networks contain layers. A layer is a group of neurons that behave similarly. There are many different layer types used by the different types of neural networks that are supported by Encog. However, there are two very important layers that nearly every neural network will have. These are the input and output layers. The input layer is how you feed data to the neural network. The output layer is how you get the response back from the neural network.
The input and output from the neural network are both C# double values, ordinary floating-point numbers. Both the input and output layers will have some number of neurons. This determines how many floating-point numbers the layer will deal with. The input and output layers will typically have a different number of neurons. Deciding the structure of the input and output layer is how you define the "problem" that you are trying to solve to the neural network.
Let's see how we could create a neural network to perform as an XOR operator. The XOR operator requires that the two inputs be different, for the output to be true. The XOR operator's truth table can be expressed as follows:
0 XOR 0 = 0
1 XOR 0 = 1
0 XOR 1 = 1
1 XOR 1 = 0
I would like to now create a neural network that can perform this operator. Such a network will have two input neurons and one output neuron. It will accept the two operands and return the result.
Using the Code
We will now take a look at how the code for this example is constructed. This example was created with Encog v2.3, which is the current version of Encog at the time of this writing. The Encog 2.3 DLL file is provided with the download for this example. You also need the log4net file which is included, as well. You may wish to grab the latest Encog JAR from the URL provided earlier in this article.
This example is packaged as a simple Visual Studio project.
Neural networks must be trained before they are of any use. To train this neural network, me must provide training data. The training data is the truth table for the XOR operator. The XOR has the following inputs:
public static double[][] XOR_INPUT ={
new double[2] { 0.0, 0.0 },
new double[2] { 1.0, 0.0 },
new double[2] { 0.0, 1.0 },
new double[2] { 1.0, 1.0 } };
These are all of the possible inputs to the XOR operator. Likewise, the expected outputs are also stored as an array.
public static double[][] XOR_IDEAL = {
new double[1] { 0.0 },
new double[1] { 1.0 },
new double[1] { 1.0 },
new double[1] { 0.0 } };
These two arrays will be combined to create the training data for the XOR operator. The following line of code combines these two arrays to create training data:
INeuralDataSet trainingSet = new BasicNeuralDataSet(XOR_INPUT, XOR_IDEAL);
We must now create a neural network. The following lines of code do this:
BasicNetwork network = new BasicNetwork();
network.AddLayer(new BasicLayer(new ActivationSigmoid(), true, 2));
network.AddLayer(new BasicLayer(new ActivationSigmoid(), true, 6));
network.AddLayer(new BasicLayer(new ActivationSigmoid(), true, 1));
network.Structure.FinalizeStructure();
network.Reset();
You can see the three layers being created. The three AddLayer methods above create the three layers. The first layer is the input layer, it has two neurons. The final layer created is the output layer, it has a single neuron. The layer created in the middle is called the hidden layer. The hidden layer helps the rest of the neural network learn. More hidden neurons must be added to allow the neural network to learn more complex patterns. Four hidden neurons is more than enough for the XOR operator. Picking the number of hidden neurons is usually a process of trial and error.
The call to the Reset method above randomizes the weights between all of the neurons in the network. These random weights will not allow the neural network to function as an XOR operator. However, the training process, that we will see shortly, will refine these weights and encourage the neural network to produce output similar to the XOR operator.
The ActivationSigmoid class specifies the type of activation that is to be used. The sigmoid function is a good choice here because we use no negative values on the XOR operator. If the network needs to recognize negative, the hyperbolic tangent activation function would be more appropriate. Encog supports a number of different activation functions, all of which have their unique uses.
A training object must be created to train the neural network. Encog supports a number of different training methods. Some are used for specific neural network types. Others perform better on different types of data. The best 'general purpose' trainer for this type of neural network is called resilient propagation (RPROP). The following code creates an RPROP trainer:
ITrain train = new ResilientPropagation(network, trainingSet);
Once the trainer has been created, we should loop through a series of iterations. Each iteration will take the neural network closer to being able to function as an XOR operator.
do
{
train.Iteration();
Console.WriteLine("Epoch #" + epoch + " Error:" + train.Error);
epoch++;
} while ((epoch < 5000) && (train.Error > 0.001));
At each iteration, or epoch, we check the error. We continue until the error is less than 1%. The error defines how far the output of the neural network is from the ideal output defined earlier.
Once the neural network has been trained satisfactorily, we will make use of it. We will feed each of the inputs into the neural network and observe the output. The following code does this:
Console.WriteLine("Neural Network Results:");
foreach (INeuralDataPair pair in trainingSet)
{
INeuralData output = network.Compute(pair.Input);
Console.WriteLine(pair.Input[0] + "," + pair.Input[1]
+ ", actual=" + output[0] + ",ideal=" + pair.Ideal[0]);
}
We loop through each of the training data items and present the output from the neural network as well as the actual output. The output from the program is shown here:
Epoch #1 Error:0.577117664847525
Epoch #2 Error:0.577117664847525
Epoch #3 Error:0.533613696022388
Epoch #4 Error:0.503211450802659
Epoch #5 Error:0.503000549513747
Epoch #6 Error:0.502288740107349
...
Epoch #40 Error:0.0206168956797096
Epoch #41 Error:0.00842597610945368
Epoch #42 Error:0.0011283298276187
Epoch #43 Error:0.000212804226087766
Neural Network Results:
0,0, actual=7.79044815631158E-07,ideal=0
1,0, actual=0.999959847028804,ideal=1
0,1, actual=0.999974904416701,ideal=1
1,1, actual=0.000101466036536172,ideal=0
As you can see, the neural network loops through a number of iterations before the error percent drops below 1%. After 43 iterations, the network is trained. When you run the application, it may take more or less, as the neural network starts with random weights.
Once it is done, you see the actual output from the neural network. The output from the neural network does not exactly match the ideal output. This is expected. However, the value 0.99 is very close to 1.0. Likewise, the scientific notation number displayed for the first pattern is close to zero.
Points of Interest
This article demonstrated a very simple neural network application. It is massive overkill to use a neural network to create an XOR operator. There are many more complex examples provided with Encog. I will likely write further articles here demonstrating some of the more advanced features of Encog.
One of the interesting features of a neural network is that it is created completely differently from a traditional program. For a traditional program, you would think about how to implement the XOR operator and create all of the necessary programming logic to do it. For a neural network, you just provide input examples and the expected outputs. It is up to the neural network to learn how to provide these expected outputs. Usually, you really have no idea how it actually learns to provide its output. This is especially true with large neural networks that may have hundreds of neurons.
