Linear Equation Solver in C#

• Download csEquationSolver.zip - 77.3 KB

Please read the section titled Known Issues further below before reporting bugs for this application.

Introduction  

Program csEquationSolver solves simultaneous equations.  The program has a single rich-text control that allows loading text, saving text, and printing text.  The text can be anything, but is intended to be a set of simultaneous equations.

The user enters the equations on the input form and then uses the Operation/Solve menu item to solve the equations.

The purpose of this is to demonstrate using the generic SparseArray class for a vector, the generic Sparse2DMatrix class as a matrix, and the LinearEquationSolver class.   The code uses a crude parser to parse simple equations.  It's crude because it requires a somewhat rigid input format and doesn't support parenthesis or math functions.

The user enters equations in the form using the following format, which allows using the addition and subtraction sign to combine terms of the form:

 [number][variable] 

The square brackets indicate the the number or variable are optionals, but there must be at least one of these in a term.  There must also be a single equals sign in the equations and at least one term on each side of the equals sign.

Either the number or variable are optional and as many terms as desired can be combined using either the plus sign or a minus sign.  The number can contain a decimal point and an exponent.   Variables can only contain alphabetic characters or the underscore character.  Floating point exponents are preceded by the ^ character instead of the usual E character to avoid any ambiguity with variable names.   The following line shows a floating point number equal to 2.3 million.

X = 2.3^6

An equation must contain an equals sign.  An equation ends at a newline character.

An example set of equations is: 

3  X + 4 Y = -5 Z
X + Z = 10 Y
X + Z = 42.5  

The program produces the solution for those equations:

X = 114.75
Y = 4.25
Z = -72.25

 Another example set of equations might be:

MARYS_AGE=2BOBS_AGE
BOBS_AGE = 3 CATHYS_AGE
CATHYS_AGE = 4 D
D = 2 

or another example:

HEIGHT = 5 + 10 

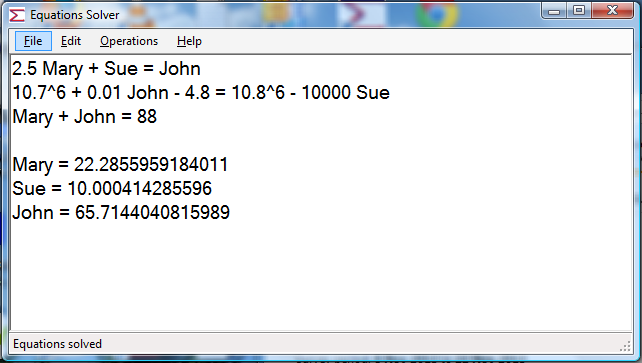
Below is the program immediately  after solving three equations.  Once solved, trying to solve the equations again will fail because there are then 6 equations and only 3 variables!  If one of the original equations is wrong, delete the solution, edit that equation, and use the Operations/Solve menu item to solve the equations again.

Background   

When I was in college, I wrote a circuit analysis program in Fortran.  I needed a way to solve simultaneous equations, and I stumbled on the following book and algorithm: 

"The solution of ill-conditioned linear equations", by J. H. Wilkinson, "Mathematical Methods For Digital Computers" Volume 2, Edited by Anthony Ralston and Herbert S. Wilf, 1967, John Wiley and Sons, pages 65-93.

An ill-conditioned set of equations is a set of equations that is either difficult or impossible to solve using the given floating point precision.

I was lucky to stumble on this particular reference.  While this book gives a standard implementation of Gaussian Elimination with partial pivoting, as is taught in Computer Science Linear Algebra courses, this algorithm also determines whether an accurate solution can be found.  This is done using both the matrix norms and a constant that is set based on the number of bits in the mantissa of a floating point number.

I've rewritten this algorithm several times.  I wrote this in Fortran, C++ using simple arrays, again in C++ using a sparse container classes, and finally in C# using a SparseArray and a Sparse2DMatrix.  The SparseArray and Sparse2DMatrix are in another codeproject article I posted earlier that also provides other higher-dimension sparse containers.

Back in the late 1970s, I ran this algorithm on a DEC-10 computer and solved 1000 equations with 1000 variables in about 30 seconds.  Today, with that original C code, a problem that size on a PC runs in the blink of an eye.  This code is slower because it's not C, but it is still very fast.

File List

• Program.cs                                               - The main program file.
• LinearEquationParser.cs                            - Parses the equations to populate a matrix and a vector and saves a list of the variable names.
• LinearEquationParserStatusInterpreter.cs  - Provides text messages based on parser status values.
• LinearEquationSolver.cs                            - Solve the matrix equations.
• Sparse2DMatrix.cs                                    - A sparse 2 dimensional matrix.
• ComparableTuple2.cs                               - Use by the sparse 2 dimensional matrix  to store indices.
• SparseArray.cs                                          - A sparse vector
• csEquationsSolver.ico                               - Stores several sizes of icons for the application.
• EquationsSolverForm.cs                           - The main form class that hosts controls.
• EquationsSolverForm.Designer.cs             - Form information
• EquationsSolverForm.resx                        - Form resources
• app.config                                               - Contains XML configuration data.
• csEquationSolver.csproj                           - The Visual Studio C# project file
• csEquationSolver.sln                                - The Visual Studio C# solution file 

Property Files

• AssemblyInfo.cs                                       - Stores text and a GUID for the .NET program assembly
• Resources.Designer.cs                              - Stores resources design information for the program.
• Resources.resx                                         - Stores resources for the program.
• Settings.Designer.cs                                 - Stores settings design information for the program.
• Settings.settings                                      - Stores settings for the program. 

About the Linear Equation Solver Class

A set of Linear equations are represented by the matrix equation:

aMatrix xVector = bVector 

The aMatrix and bVector are given, and the xVector is the solution.

The article makes the second terms, xVector and bVector matrices, so, after performing certain calculations on the aMatrix, the original algorithm could can solve multiple sets of equations with several different bVectors in a matrix efficiently.  I simplified algorithm to only solves a single set of equations by removing a loop in the final step of the algorithm.

3 X +  4 Y + 5 Z = 0
1 X - 10 Y + 1 Z = 0
1 X +  0 Y + 1 Z = 42.5   

The matrix form of these equations is:

| 3   4  5 | | X |   |   0  |
| 1  10  1 | | Y | = |   0  |
| 1   0  1 | | Z |   | 42.5 |

The aMatrix is the square matrix on the left.  The bVector is on the right. 

The xVector, which contains the variable names, which are the unknowns, is in the middle.

To solve these equations, call the Solver method of the LinearEquationSolver class.  The class signature is:

public static LinearEquationSolverStatus Solve(int numberOfEquations, 
                                               Sparse2DMatrix<int, int, double> aMatrix,
                                               SparseArray<int, double> bVector,
                                               SparseArray<int, double> xVector)

Note the different order of the arguments from the equation above.  The xVector, which will store the solution, is the last argument.  The number of equations is the size of one dimension of the square matrix.

The program will also indicate if a set of equations is 'singular' to working accuracy.   A singular set of equations has no single solution because two or more equations are merely a multiple of the other equation, such as:

X + Y = 7
2X + 2Y = 36

Even  if the second equation was, "2X + 2Y = 14", so it was consistent with the first equation, there is no single solution to the two equations, and the program would report that the equations were singular to working accuracy.

An Important Parameter For Determining If Equations Are Ill-Conditioned

The LinearEquationSolver class has a constant that is set based on the number of bits in the mantissa of a double precision floating point number.  If you port the linear equation solver to another platform, then be sure to adjust this constant.  The LinearEquationSolver code contains the following regarding this issue:

// The original implementation was on a computer where the floating
// point mantissa was 39 bits.  For that system, the value below
// was set to 2.92E-11, which is just slightly larger than
// 1/(2^35), which is 2.91E-11.  For my Intel system, the mantissa
// of a double precision floating point number is 48 bits, so
// the value is set to slightly greater than 1/(2^44).  1/(s^44)
// evaluates to 5.68E-14, so the value 5.69E-14 is used here.
public static readonly double s_smallFloatingPointValue = 5.69E-14; 

The Solver routine in file EquationsSolverForm.cs

The Solver method is the primary method in the program.  This is called when the user clicks on the "Solve" submenu of the "Operations" menu to solve the set of equations in the rich-text box.  The solution is written into the rich-text box, so trying to solve again without deleting the solution text will result in an error message.

There are three steps in the Solve method.  First a LinearEquationParser.Parse method is called to fill in the aMatrix and bVector, and then the LinearEquationSolver.Solve method is called to solve the equations.  Finally the solution data is output into the rich text control or an error message is displayed.

See file EquationsSolverForm.cs for the rest of the form code.

    private void Solve()
    {
        mainToolStripStatusLabel.Text = Properties.Resources.IDS_SOLVING_EQUATIONS;

        Sparse2DMatrix<int, int, double> aMatrix = new Sparse2DMatrix<int, int, double>();
        SparseArray<int, double> bVector = new SparseArray<int, double>();
        SparseArray<string, int> variableNameIndexMap = new SparseArray<string, int>();
        int numberOfEquations = 0;

        LinearEquationParser parser = new LinearEquationParser();
        LinearEquationParserStatus parserStatus = LinearEquationParserStatus.Success;

        foreach (string inputLine in equationsRichTextBox.Lines)
        {
            parserStatus = parser.Parse(inputLine,
                                        aMatrix,
                                        bVector,
                                        variableNameIndexMap,
                                        ref numberOfEquations);

            if (parserStatus != LinearEquationParserStatus.Success)
            {
                break;
            }
        }

        // Assume success.
        string mainStatusBarText = Properties.Resources.IDS_EQUATIONS_SOLVED;

        // Did an error occur?
        if (parserStatus == LinearEquationParserStatus.Success)
        {
            // Are there the same number of equations as variables?
            if (numberOfEquations == variableNameIndexMap.Count)
            {
                // Create a solution vector.
                SparseArray<int, double> xVector = new SparseArray<int, double>();

                // Solve the simultaneous equations.
                LinearEquationSolverStatus solverStatus =
                    LinearEquationSolver.Solve(numberOfEquations,
                                               aMatrix,
                                               bVector,
                                               xVector);

                if (solverStatus == LinearEquationSolverStatus.Success)
                {
                    string solutionString = "";

                    foreach (KeyValuePair<string, int> pair in variableNameIndexMap)
                    {
                        solutionString += string.Format("{0} = {1}", pair.Key, xVector[pair.Value]);
                        solutionString += "\n";
                    }

                    equationsRichTextBox.Text += "\n" + solutionString;
                }
                else if (solverStatus == LinearEquationSolverStatus.IllConditioned)
                {
                    mainStatusBarText = Properties.Resources.IDS_ILL_CONDITIONED_SYSTEM_OF_EQUATIONS;
                }
                else if (solverStatus == LinearEquationSolverStatus.Singular)
                {
                    mainStatusBarText = Properties.Resources.IDS_SINGULAR_SYSTEM_OF_EQUATIONS;
                }
            }
            else if (numberOfEquations < variableNameIndexMap.Count)
            {
                mainStatusBarText = string.Format(Properties.Resources.IDS_TOO_FEW_EQUATIONS,
                                                  numberOfEquations, variableNameIndexMap.Count);
            }
            else if (numberOfEquations > variableNameIndexMap.Count)
            {
                mainStatusBarText = string.Format(Properties.Resources.IDS_TOO_MANY_EQUATIONS,
                                                  numberOfEquations, variableNameIndexMap.Count);
            }
        }
        else
        {
            // An error occurred. Report the error in the status bar.
            mainStatusBarText = LinearEquationParserStatusInterpreter.GetStatusString(parserStatus);
        }

        mainToolStripStatusLabel.Text = mainStatusBarText;
    }
} 

The LinearEquationSolver Class in file LinearEquationSolver.cs

This method implements Gaussian Elimination with partial pivoting, and then does an iterative refining of the solution vector by computing residuals.  For more detail, consult the reference I listed in the Background section of this article above.

//=======================================================================
// Copyright (C) 2010-2013 William Hallahan
//
// Permission is hereby granted, free of charge, to any person
// obtaining a copy of this software and associated documentation
// files (the "Software"), to deal in the Software without restriction,
// including without limitation the rights to use, copy, modify, merge,
// publish, distribute, sublicense, and/or sell copies of the Software,
// and to permit persons to whom the Software is furnished to do so,
// subject to the following conditions:
//
// The above copyright notice and this permission notice shall be
// included in all copies or substantial portions of the Software.
//
// THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND,
// EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES
// OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
// NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT
// HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY,
// WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
// FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR
// OTHER DEALINGS IN THE SOFTWARE.
//=======================================================================

//======================================================================
//  File: LinearEquationSolver.cpp
//  Author: Bill Hallahan
//  Date: April 13, 2010
//======================================================================

using System;
using System.Text;
using SparseCollections;
using Mathematics;

namespace Mathematics
{
    enum LinearEquationSolverStatus
    {
        Success,
        IllConditioned,
        Singular,
    };

    /// <summary>
    /// This class solves systems of linear equations.
    /// </summary>
    class LinearEquationSolver
    {
        // The original implementation was on a computer where the floating
        // point mantissa was 39 bits.  For that system, the value below
        // was set to 2.92E-11, which is just slightly larger than
        // 1/(2^35), which is 2.91E-11.  For my Intel system, the mantissa
        // of a double precision floating point number is 48 bits, so
        // the value is set to slightly greater than 1/(2^44).  1/(s^44)
        // evaluates to 5.68E-14, so the value 5.69E-14 is used here.
        public static readonly double s_smallFloatingPointValue = 5.69E-14;

        /// <summary>
        /// This function solves simultaneous equations in matrix form.
        /// The equations are represented by the matrix equation:
        /// 
        ///     aMatrix xVector = bVector
        ///
        /// The algorithm is from the book:
        /// "Mathematical Methods For Digital Computers" Volume 2
        /// Edited by Anthony Ralston and Herbert S. Wilf, 1967,
        /// John Wiley and Sons, pages 65-93.
        /// "The solution of ill-conditioned linear equations"
        /// by J. H. Wilkinson.
        /// </summary>
        /// <param name="numberOfEquations">The number of equations</param>
        /// <param name="aMatrix">A square matrix</param>
        /// <param name="bVector">A vector that contains the right hand side of the matrix equations shown below.</param>
        /// <param name="xVector">A vector to contain the solution of the matrix equations.</param>
        /// <returns>
        /// This function returns an enumerated value of type Status_T
        /// that is the value LinearEquationSolverStatus.Singular if the
        /// coefficient matrix is singular to working accuracy. A value of
        /// LinearEquationSolverStatus.IllConditioned is returned if the
        /// coefficient matrix is singular to working accuracy, i.e. the
        /// floating point arithmetic does not have enough precision to
        /// guarantee convergence to an accurate solution.
        /// The value LinearEquationSolverStatus.Success is returned
        /// if the solution vector was calculated successfully.
        /// </returns>
        public static LinearEquationSolverStatus Solve(int numberOfEquations,
                                                       Sparse2DMatrix<int, int, double> aMatrix,
                                                       SparseArray<int, double> bVector,
                                                       SparseArray<int, double> xVector)
        {
            //----------------------------------------------------------
            // Matrix a_matrix is copied into working matrix aMatrixCopy.
            //----------------------------------------------------------

            Sparse2DMatrix<int, int, double> aMatrixCopy = new Sparse2DMatrix<int, int, double>(aMatrix);

            //----------------------------------------------------------
            // The maximum value rowMaximumVector[i], i = 0 to n - 1
            // is stored
            //----------------------------------------------------------

            SparseArray<int, double> rowMaximumVector = new SparseArray<int, double>();

            int i = 0;
            for (i = 0; i < numberOfEquations; i++)
            {
                double temp = 0.0;

                for (int j = 0; j < numberOfEquations; j++)
                {
                    double test = Math.Abs(aMatrix[i, j]);
                    
                    if (test > temp)
                    {
                        temp = test;
                    }
                }

                rowMaximumVector[i] = temp;

                //----------------------------------------------------------
                // Test for singular matrix.
                //----------------------------------------------------------

                if (temp == 0.0)
                {
                    return LinearEquationSolverStatus.Singular;
                }
            }

            //----------------------------------------------------------
            // The r'th column of "l", the r'th pivotal position r', and
            // the r'th row of "u" are determined.
            //----------------------------------------------------------

            SparseArray<int, int> pivotRowArray = new SparseArray<int, int>();

            for (int r = 0; r < numberOfEquations; r++)
            {
                double maximumValue = 0.0;
                int rowMaximumValueIndex = r;

                //----------------------------------------------------------
                // The l[i][r], i = r to n - 1 are determined.
                // l[i][r] is a lower triangular matrix. It is calculated
                // using the variable temp and copied into matrix
                // "aMatrixCopy". The variable "maximumValue" contains
                // the largest Math.Abs(l[i][r] / pivotRowArray[i]) and
                // rowMaximumValueIndex stores the "i" which corresponds
                // to the value in variable maximumValue.
                //----------------------------------------------------------

                double temp;

                for (i = r; i < numberOfEquations; i++)
                {
                    temp = aMatrixCopy[i, r];

                    for (int j = 0; j < r; j++)
                    {
                        temp = temp - aMatrixCopy[i, j] * aMatrixCopy[j, r];
                    }

                    aMatrixCopy[i, r] = temp;

                    double test = Math.Abs(temp / rowMaximumVector[i]);

                    if (test > maximumValue)
                    {
                        maximumValue = test;
                        rowMaximumValueIndex = i;
                    }
                }

                //----------------------------------------------------------
                // Test for matrix which is singular to working precision.
                //----------------------------------------------------------

                if (maximumValue == 0.0)
                {
                    return LinearEquationSolverStatus.IllConditioned;
                }

                //----------------------------------------------------------
                // "rowMaximumValueIndex" = r' and "pivotRowArray[r]"
                // is the pivotal row.
                //----------------------------------------------------------

                rowMaximumVector[rowMaximumValueIndex] = rowMaximumVector[r];
                pivotRowArray[r] = rowMaximumValueIndex;

                //----------------------------------------------------------
                // Rows "r" and "pivotRowArray[r]" are exchanged.
                //----------------------------------------------------------

                for (i = 0; i < numberOfEquations; i++)
                {
                    temp = aMatrixCopy[r, i];
                    aMatrixCopy[r, i] = aMatrixCopy[rowMaximumValueIndex, i];
                    aMatrixCopy[rowMaximumValueIndex, i] = temp;
                }

                //----------------------------------------------------------
                // The u[r][i], i = r + 1 to n - 1 are determined.
                // "u[r][i]" is an upper triangular matrix. It is copied
                // into aMatrixCopy.
                //----------------------------------------------------------

                for (i = r + 1; i < numberOfEquations; i++)
                {
                    temp = aMatrixCopy[r, i];

                    for (int j = 0; j < r; j++)
                    {
                        temp = temp - aMatrixCopy[r, j] * aMatrixCopy[j, i];
                    }

                    aMatrixCopy[r, i] = temp / aMatrixCopy[r, r];
                }
            }

            //----------------------------------------------------------
            // The first solution vector is set equal to the null vector
            // and the first residuals are set equal to the equation
            // constant vector.
            //----------------------------------------------------------

            SparseArray<int, double> residualVector = new SparseArray<int, double>();

            for (i  = 0; i < numberOfEquations; i++)
            {
                xVector[i] = 0.0;
                residualVector[i] = bVector[i];
            }

            //----------------------------------------------------------
            // The iteration counter is initialized.
            //----------------------------------------------------------

            int iteration = 0;
            bool notConvergedFlag = true;

            do
            {
                //----------------------------------------------------------
                // The forward substitution is performed and the solution
                // of l y = p r is calculated where p r is the current
                // residual after interchanges.
                //----------------------------------------------------------

                for (i = 0; i < numberOfEquations; i++)
                {
                    int pivotRowIndex = pivotRowArray[i];
                    double temp = residualVector[pivotRowIndex];
                    residualVector[pivotRowIndex] = residualVector[i];

                    for (int j = 0; j < i; j++)
                    {
                        temp = temp - aMatrixCopy[i, j] * residualVector[j];
                    }

                    residualVector[i] = temp / aMatrixCopy[i, i];
                }

                //----------------------------------------------------------
                // The back substitution is performed and the solution of
                // u e = y is calculated. The current correction is stored
                // in variable residualVector.
                //----------------------------------------------------------

                for (i = numberOfEquations - 1; i >= 0; i--)
                {
                    double temp = residualVector[i];

                    for (int j = i + 1; j < numberOfEquations; j++)
                    {
                        temp = temp - aMatrixCopy[i, j] * residualVector[j];
                    }

                    residualVector[i] = temp;
                }

                //----------------------------------------------------------
                // The norm of the error in the residuals and the norm of
                // the present solution vector are calculated.
                //----------------------------------------------------------

                double normOfX = 0.0;
                double normOfError = 0.0;

                for (i = 0; i < numberOfEquations; i++)
                {
                    double test = Math.Abs(xVector[i]);

                    if (test > normOfX)
                    {
                        normOfX = test;
                    }

                    test = Math.Abs(residualVector[i]);

                    if (test > normOfError)
                    {
                        normOfError = test;
                    }
                }

                //----------------------------------------------------------
                // If iteration is zero then skip this section because
                // no correction exists on the first iteration.
                //----------------------------------------------------------

                if (iteration != 0)
                {
                    //------------------------------------------------------
                    // Test for matrix which is singular to working
                    // precision.
                    //------------------------------------------------------

                    if ((iteration == 1) && (normOfError / normOfX > 0.5))
                    {
                        return LinearEquationSolverStatus.IllConditioned;
                    }

                    //------------------------------------------------------
                    // Check to see if "normOfError" / "normOfX" is greater
                    // than 2 ^ (1 - t), where "t" is the number of bits
                    // in the mantissa of a double precision number. If
                    // this is not true then the last correction is almost
                    // negligible and "notConvergedFlag" is set to false.
                    //------------------------------------------------------

                    notConvergedFlag = normOfError / normOfX >= s_smallFloatingPointValue;

    #if DEBUGCODE
                    double normRatioForDebug = normOfError / normOfX;
    #endif
                }

                //----------------------------------------------------------
                // The corrections (residuals) are added to the
                // solution vector.
                //----------------------------------------------------------

                for (i = 0; i < numberOfEquations; i++)
                {
                    xVector[i] = xVector[i] + residualVector[i];
                }

                //----------------------------------------------------------
                // The new residuals corresponding to the solution vector
                // are calculated.
                //----------------------------------------------------------

                for (i = 0; i < numberOfEquations; i++)
                {
                    double temp = bVector[i];

                    for (int j = 0; j < numberOfEquations; j++)
                    {
                        temp = temp - aMatrix[i, j] * xVector[j];
                    }

                    residualVector[i] = temp;
                }

                //----------------------------------------------------------
                // The iteration counter is incremented and the flag
                // "notConvergedFlag" is tested. If notConvergedFlag is false
                // then the solution vector has converged to sufficient
                // accuracy.
                //----------------------------------------------------------

                iteration++;
            }
            while (notConvergedFlag);

            return LinearEquationSolverStatus.Success;
        }
    }
}

 The  (crude) LinearEquationParser class in file LinearEquationParser.cs

//=======================================================================
// Copyright (C) 2010-2013 William Hallahan
//
// Permission is hereby granted, free of charge, to any person
// obtaining a copy of this software and associated documentation
// files (the "Software"), to deal in the Software without restriction,
// including without limitation the rights to use, copy, modify, merge,
// publish, distribute, sublicense, and/or sell copies of the Software,
// and to permit persons to whom the Software is furnished to do so,
// subject to the following conditions:
//
// The above copyright notice and this permission notice shall be
// included in all copies or substantial portions of the Software.
//
// THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND,
// EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES
// OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
// NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT
// HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY,
// WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
// FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR
// OTHER DEALINGS IN THE SOFTWARE.
//=======================================================================

//======================================================================
// Class File: LinearEquationParser.cs
// Author: Bill Hallahan
// Date: April 13, 2010
//======================================================================

using System;
using System.Text;
using SparseCollections;

namespace Mathematics
{
    public enum LinearEquationParserStatus
    {
        Success,
        SuccessNoEquation,
        ErrorIllegalEquation,
        ErrorNoEqualSign,
        ErrorMultipleEqualSigns,
        ErrorNoTermBeforeEqualSign,
        ErrorNoTermAfterEqualSign,
        ErrorNoTermEncountered,
        ErrorNoVariableInEquation,
        ErrorMultipleDecimalPoints,
        ErrorTooManyDigits,
        ErrorMissingExponent,
        ErrorIllegalExponent,
    }

    internal enum LinearEquationParserState
    {
        ParseTerm,
        ParseOperator
    };

    /// <summary>
    /// This class provides a parser for strings that contain a system
    /// of linear equations that constructs the matrix equations needed
    /// to solve the system of equations.
    /// </summary>
    public class LinearEquationParser
    {
        private static readonly int m_maximumNumberLength = 20;

        private int m_startPosition;
        private int m_equationIndex;
        private LinearEquationParserState m_parserState;
        private bool m_negativeOperatorFlag;
        private bool m_equalSignInEquationFlag;
        private bool m_atLeastOneVariableInEquationFlag;
        private bool m_termBeforeEqualSignExistsFlag;
        private bool m_termAfterEqualSignExistsFlag;


        /// <summary>
        /// This property returns the last status value of the parser.
        /// </summary>
        /// <returns>A value of type LinearEquationParserStatus</returns>
        public LinearEquationParserStatus LastStatusValue
        {
            get;
            set;
        }

        /// <summary>
        /// This property gets the position in the input line where the last
        /// error occurred.  This should only be invoked if the Parser() method
        /// returns an error status value.
        /// </summary>
        /// <returns>The position in the input line where an error occurred</returns>
        public int ErrorPosition
        {
            get;
            set;
        }

        /// <summary>
        /// Constructor
        /// </summary>
        public LinearEquationParser()
        {
            Reset();
        }


        /// <summary>
        /// Destructor
        /// </summary>
        ~LinearEquationParser()
        {
        }

        /// <summary>
        /// This function parses line that contains all or part of a simple
        /// linear equation. The equation contains terms separated by operators.
        /// The term can be a number, a variable, or a number and a variable.
        /// A term cannot be split between lines input to the parser method.
        /// The operators are either the plus character '+', the minus
        /// character '-', or the equal sign character '='.  Numbers can have
        /// up to 15 digits, a decimal point, and an exponent of a power
        /// of 10 that follows the '^' character.
        /// </summary>
        /// <param name="inputLine">The input line of text to be parsed</param>
        /// <param name="aMatrix">The A matrix for the simultaneous equations.
        /// This is updated as each line of input is parsed.
        /// </param>
        /// <param name="bVector">The B vector for the simultaneous equations.
        /// This is updated as each line of input is parsed.</param>
        /// <param name="variableNameIndexMap">A map that stores the integer
        /// index for a variable using the variable name as a key.</param>
        /// <param name="numberOfEquations">A reference to an integer that
        /// will contain the  number of equations when this method exits.
        /// </param>
        /// <returns>An enum of type LinearEquationParserStatus</returns>
        public LinearEquationParserStatus Parse(string inputLine,
                                                Sparse2DMatrix<int, int, double> aMatrix,
                                                SparseArray<int, double> bVector,
                                                SparseArray<string, int> variableNameIndexMap,
                                                ref int numberOfEquations)
        {
            //------------------------------------------------------------------
            // Trim any space characters from the end of the line.
            //------------------------------------------------------------------

            inputLine.TrimEnd(null);

            //------------------------------------------------------------------
            // Assume success status.
            //------------------------------------------------------------------

            int positionIndex = 0;
            SetLastStatusValue(LinearEquationParserStatus.Success, positionIndex);

            //------------------------------------------------------------------
            // Skip whitespace characters
            //------------------------------------------------------------------

            SkipSpaces(inputLine, ref positionIndex);

            //------------------------------------------------------------------
            // Save the position of the first non-whitespace character. If
            // the first term is not found at this position then set the
            // error status to report that it is likely that the last
            // equation was not properly terminated.
            //------------------------------------------------------------------

            m_startPosition = positionIndex;

            //------------------------------------------------------------------
            // Separate the input string into tokens.
            //
            // Variables contains the letters A through Z and the underscore
            // '_' character.
            //
            // Operators include plus '+', minus '-', and times '*'.
            //
            // Delimiters include the equals sign '='.
            //
            // Numbers include the digits 0 through 9, the decimal point
            // (period character) '.', an optional exponent character which
            // is the letter '^', and up to two digits for the optional exponent.
            //
            // Check for sequences of terms and operators.
            //
            // Term:
            //   <Space> <Sign> Number <Space>
            //   <Space> <Sign> Variable <Space>
            //   <Space> <Sign> Number Variable <Space>
            //
            // Operator:
            //   <Space> Plus <Space>
            //   <Space> Minus <Space>
            //   <Space> Equals <Space>
            //
            //--------------------------------------------------------------

            bool operatorFoundLast = false;

            while (positionIndex < inputLine.Length)
            {
                if (m_parserState == LinearEquationParserState.ParseTerm)
                {
                    //------------------------------------------------------
                    // Skip whitespace characters
                    //------------------------------------------------------

                    SkipSpaces(inputLine, ref positionIndex);

                    if (positionIndex < inputLine.Length)
                    {
                        if (GetTerm(inputLine,
                                    ref positionIndex,
                                    aMatrix,
                                    bVector,
                                    variableNameIndexMap))
                        {
                            m_parserState = LinearEquationParserState.ParseOperator;
                            operatorFoundLast = false;
                        }
                        else
                        {
                            if (LastStatusValue == LinearEquationParserStatus.Success)
                            {
                                SetLastStatusValue(LinearEquationParserStatus.ErrorIllegalEquation,
                                                   positionIndex);
                            }

                            break;
                        }
                    }
                    else
                    {
                        break;
                    }
                }
                else if (m_parserState == LinearEquationParserState.ParseOperator)
                {
                    //------------------------------------------------------
                    // Skip whitespace characters
                    //------------------------------------------------------

                    SkipSpaces(inputLine, ref positionIndex);

                    if (positionIndex < inputLine.Length)
                    {
                        //------------------------------------------------------
                        // Check for plus sign, minus sign, or an equal sign.
                        //------------------------------------------------------

                        if (GetOperator(inputLine, ref positionIndex))
                        {
                            m_parserState = LinearEquationParserState.ParseTerm;
                            operatorFoundLast = true;
                        }
                        else
                        {
                            if (LastStatusValue != LinearEquationParserStatus.Success)
                            {
                                if (positionIndex == m_startPosition)
                                {
                                    SetLastStatusValue(LinearEquationParserStatus.ErrorIllegalEquation,
                                                       positionIndex);
                                }
                            }

                            break;
                        }
                    }
                }
            }

            // If an operator was found at 
            if ((positionIndex >= inputLine.Length) && (positionIndex > 0) && (!operatorFoundLast))
            {
                ResetForNewEquation();
                numberOfEquations = m_equationIndex;
            }

            return LastStatusValue;
        }

        /// <summary>
        /// This function resets the parser to its initial state for parsing
        /// a new set of simultaneous linear equations.
        /// </summary>
        void Reset()
        {
            m_startPosition = 0;
            ErrorPosition = 0;
            LastStatusValue =  LinearEquationParserStatus.Success;
            m_negativeOperatorFlag = false;
            m_equalSignInEquationFlag = false;
            m_atLeastOneVariableInEquationFlag = false;
            m_termBeforeEqualSignExistsFlag = false;
            m_termAfterEqualSignExistsFlag = false;
            m_parserState = LinearEquationParserState.ParseTerm;
            m_equationIndex = 0;
        }

        /// <summary>
        /// This function calculate the status value for an incomplete equation.
        /// This should be called if the IsCompleteEquation() method returns false.
        /// </summary>
        /// <returns>An enum value of type 'LinearEquationParserStatus'</returns>
        private LinearEquationParserStatus GetEquationStatus()
        {
            LinearEquationParserStatus status = LinearEquationParserStatus.Success;

            if ((!m_equalSignInEquationFlag)
                && (!m_termBeforeEqualSignExistsFlag)
                && (!m_termAfterEqualSignExistsFlag)
                && (!m_atLeastOneVariableInEquationFlag))
            {
                status = LinearEquationParserStatus.SuccessNoEquation;
            }
            else if (!m_equalSignInEquationFlag)
            {
                status = LinearEquationParserStatus.ErrorNoEqualSign;
            }
            else if (!m_termBeforeEqualSignExistsFlag)
            {
                status = LinearEquationParserStatus.ErrorNoTermBeforeEqualSign;
            }
            else if (!m_termAfterEqualSignExistsFlag)
            {
                status = LinearEquationParserStatus.ErrorNoTermAfterEqualSign;
            }
            else if (!m_atLeastOneVariableInEquationFlag)
            {
                status = LinearEquationParserStatus.ErrorNoVariableInEquation;
            }
            else
            {
                status = LinearEquationParserStatus.Success;
            }

            return status;
        }


        /// <summary>
        /// This function resets the parser to process a new equation.
        /// </summary>
        private void ResetForNewEquation()
        {
            m_startPosition = 0;
            m_negativeOperatorFlag = false;
            m_equalSignInEquationFlag = false;
            m_atLeastOneVariableInEquationFlag = false;
            m_termBeforeEqualSignExistsFlag = false;
            m_termAfterEqualSignExistsFlag = false;
            m_parserState = LinearEquationParserState.ParseTerm;
            m_equationIndex++;
        }

        /// <summary>
        /// This method gets a term in the simultaneous equation. The term
        /// can be a number, a variable, or a number and a variable. A term
        /// cannot be split between lines input to this method.
        /// </summary>
        /// <param name="inputLine">The input line to be parsed</param>
        /// <param name="positionIndex">The current parse position in the input string.</param>
        /// <param name="aMatrix">The A matrix for the simultaneous equations.
        /// This is updated as each line of input is parsed.
        /// </param>
        /// <param name="bVector">The B vector for the simultaneous equations.
        /// This is updated as each line of input is parsed.</param>
        /// <param name="variableNameIndexMap">A map that stores the integer
        /// index for a variable using the variable name as a key.</param>
        /// <returns>This method returns the value 'true' if and only if a term is found.
        /// </returns>
        private bool GetTerm(string inputLine,
                             ref int positionIndex,
                             Sparse2DMatrix<int, int, double> aMatrix,
                             SparseArray<int, double> bVector,
                             SparseArray<string, int> variableNameIndexMap)
        {
            //------------------------------------------------------------------
            // A term is one of the following three patterns.
            //
            // <Space> <Sign> Number <Space>
            // <Space> <Sign> Variable <Space>
            // <Space> <Sign> Number Variable <Space>
            //
            // Check for a plus or a minus sign at the start of a term.
            //------------------------------------------------------------------

            bool numberIsNegativeFlag = false;

            GetSign(inputLine,
                    ref positionIndex,
                    ref numberIsNegativeFlag);

            //------------------------------------------------------------------
            // Skip whitespace characters
            //------------------------------------------------------------------

            SkipSpaces(inputLine, ref positionIndex);

            //------------------------------------------------------------------
            // Check to see if this is a number or a variable.
            //------------------------------------------------------------------

            string numberString = "";

            bool haveNumberFlag = GetNumber(inputLine,
                                            ref positionIndex,
                                            ref numberString);

            //------------------------------------------------------------------
            // If an error occurred then abort.
            //------------------------------------------------------------------

            if (LastStatusValue != LinearEquationParserStatus.Success)
            {
                return false;
            }

            //------------------------------------------------------------------
            // If there was a number encountered then test to see if the
            // number has an exponent.
            //------------------------------------------------------------------

            if (haveNumberFlag)
            {
                if (positionIndex < inputLine.Length)
                {
                    //----------------------------------------------------------
                    // Does the number have an exponent?
                    //----------------------------------------------------------

                    if (inputLine[positionIndex] == '^')
                    {
                        positionIndex++;

                        //------------------------------------------------------
                        // Does the exponent have a sign.
                        //------------------------------------------------------

                        bool negativeExponentFlag = false;

                        GetSign(inputLine,
                                ref positionIndex,
                                ref negativeExponentFlag);

                        //------------------------------------------------------
                        // Get the exponent digits.
                        //------------------------------------------------------

                        string exponentString = "";

                        if (GetNumber(inputLine,
                                      ref positionIndex,
                                      ref exponentString))
                        {
                            //--------------------------------------------------
                            // Is the exponent a valid exponent.
                            //--------------------------------------------------

                            int exponentLength = exponentString.Length;

                            if (exponentLength <= 2)
                            {
                                bool exponent_error_flag = false;

                                for (int i = 0; i < exponentLength; ++i)
                                {
                                    if (!Char.IsDigit(exponentString[i]))
                                    {
                                        exponent_error_flag = true;
                                    }
                                }

                                if (!exponent_error_flag)
                                {
                                    numberString += 'E';

                                    if (negativeExponentFlag)
                                    {
                                        numberString += '-';
                                    }

                                    numberString += exponentString;
                                }
                                else
                                {
                                    SetLastStatusValue(LinearEquationParserStatus.ErrorIllegalExponent,
                                                       positionIndex);
                                    return false;
                                }
                            }
                            else
                            {
                                SetLastStatusValue(LinearEquationParserStatus.ErrorIllegalExponent,
                                                   positionIndex);
                                return false;
                            }
                        }
                        else
                        {
                            SetLastStatusValue(LinearEquationParserStatus.ErrorMissingExponent,
                                               positionIndex);
                            return false;
                        }
                    }
                }
            }

            //------------------------------------------------------------------
            // Skip whitespace characters
            //------------------------------------------------------------------

            SkipSpaces(inputLine, ref positionIndex);

            string variableName = "";

            bool haveVariableNameFlag = GetVariableName(inputLine,
                                                        ref positionIndex,
                                                        ref variableName);

            //------------------------------------------------------------------
            // Calculate the sign of the value. The sign is negated
            // if the equals sign has been encountered.
            //------------------------------------------------------------------

            bool negativeFlag =
                m_equalSignInEquationFlag ^ m_negativeOperatorFlag ^ numberIsNegativeFlag;

            double value = 0.0;

            if (haveNumberFlag)
            {
                value = Convert.ToDouble(numberString);

                if (negativeFlag)
                {
                    value = -value;
                }
            }
            else
            {
                value = 1.0;

                if (negativeFlag)
                {
                    value = -value;
                }
            }

            //------------------------------------------------------------------
            // If a variable was encountered then add to the aMatrix.
            //------------------------------------------------------------------

            bool haveTermFlag = false;

            if (haveVariableNameFlag)
            {
                //--------------------------------------------------------------
                // If either a number or a variable is found then a term was
                // found.
                //--------------------------------------------------------------

                haveTermFlag = true;

                //--------------------------------------------------------------
                // Each equation must have at least one variable.
                // Record that a variable was encountered in this equation.
                //--------------------------------------------------------------

                m_atLeastOneVariableInEquationFlag = true;

                //--------------------------------------------------------------
                // If this variable has not been encountered before then add
                // the variable to the variableNameIndexMap.
                //--------------------------------------------------------------

                int variableNameIndex = 0;

                if (!variableNameIndexMap.TryGetValue(variableName, out variableNameIndex))
                {
                    // This is a new variable. Add it to the map.
                    variableNameIndex = variableNameIndexMap.Count;
                    variableNameIndexMap[variableName] = variableNameIndex;
                }

                aMatrix[m_equationIndex, variableNameIndex] =
                    aMatrix[m_equationIndex, variableNameIndex] + value;
            }
            else if (haveNumberFlag)
            {
                //--------------------------------------------------------------
                // If either a number or a variable is found then a term was
                // found.
                //--------------------------------------------------------------
                
                haveTermFlag = true;

                //--------------------------------------------------------------
                // Put the value in the B vector.
                //--------------------------------------------------------------

                bVector[m_equationIndex] = bVector[m_equationIndex] - value;
            }
            else
            {
                haveTermFlag = false;
                SetLastStatusValue(LinearEquationParserStatus.ErrorNoTermEncountered,
                                   positionIndex);
                return false;
            }

            //------------------------------------------------------------------
            // There must be at least one term on each side of the equal sign.
            //------------------------------------------------------------------

            if (haveTermFlag)
            {
                if (m_equalSignInEquationFlag)
                {
                    m_termAfterEqualSignExistsFlag = true;
                }
                else
                {
                    m_termBeforeEqualSignExistsFlag = true;
                }
            }

            //------------------------------------------------------------------
            // Skip whitespace characters
            //------------------------------------------------------------------

            SkipSpaces(inputLine, ref positionIndex);

            return haveTermFlag;
        }

        /// <summary>
        /// This function parses a plus sign character or a minus sign character.
        /// </summary>
        /// <param name="inputLine">The input string to be parsed</param>
        /// <param name="positionIndex">A reference to the current parse position
        /// in the input string</param>
        /// <param name="negativeFlag">A reference to a boolean variable that is
        /// set to the value 'true' if and only if a minus sign is encountered.</param>
        /// <returns></returns>
        private bool GetSign(string inputLine,
                             ref int positionIndex,
                             ref bool negativeFlag)
        {
            //------------------------------------------------------------------
            // Check for a plus or a minus sign.
            //------------------------------------------------------------------

            bool haveSignFlag = false;
            negativeFlag = false;

            if (positionIndex < inputLine.Length)
            {
                char c = inputLine[positionIndex];

                if (c == '+')
                {
                    haveSignFlag = true;
                    positionIndex ++;
                }
                else if (c == '-')
                {
                    haveSignFlag = true;
                    negativeFlag = true;
                    positionIndex ++;
                }
            }

            return haveSignFlag;
        }

        /// <summary>
        /// This function parses a number string.
        /// </summary>
        /// <param name="inputLine">The input string to be parsed</param>
        /// <param name="positionIndex">A reference to the current parse position
        /// in the input string</param>
        /// <param name="numberString">A reference to a number string.</param>
        /// <returns>Returns the value 'true' if and only if a number is found.</returns>
        private bool GetNumber(string inputLine,
                               ref int positionIndex,
                               ref string numberString)
        {
            int decimalPointCount = 0;
            int digitLength = 0;
            bool haveNumberFlag = false;
            bool continueFlag = positionIndex < inputLine.Length;

            while (continueFlag)
            {
                Char c = inputLine[positionIndex];

                continueFlag = (c == '.');

                if (Char.IsDigit(c))
                {
                    if (++digitLength > m_maximumNumberLength)
                    {
                        SetLastStatusValue(LinearEquationParserStatus.ErrorTooManyDigits,
                                           positionIndex);
                        return false;
                    }

                    haveNumberFlag = true;
                    numberString += c;
                    positionIndex++;
                    continueFlag = positionIndex < inputLine.Length;
                }
                else
                {
                    continueFlag = c == '.';

                    if (continueFlag)
                    {
                        if (++decimalPointCount > 1)
                        {
                            SetLastStatusValue(LinearEquationParserStatus.ErrorMultipleDecimalPoints,
                                               positionIndex);
                            return false;
                        }

                        numberString += c;
                        positionIndex++;
                        continueFlag = positionIndex < inputLine.Length;
                    }
                }
            }

            if (numberString.Length > m_maximumNumberLength)
            {
                SetLastStatusValue(LinearEquationParserStatus.ErrorTooManyDigits,
                                   positionIndex);
                return false;
            }

            return haveNumberFlag;
        }

        /// <summary>
        /// This function parses a variable name string.
        /// </summary>
        /// <param name="inputLine">The input string to be parsed</param>
        /// <param name="positionIndex">A reference to the current parse position
        /// in the input string</param>
        /// <param name="variableName">A reference to a variable name string.</param>
        /// <returns>Returns the value 'true' if and only if a variable name is found.</returns>
        private bool GetVariableName(string inputLine,
                                     ref int positionIndex,
                                     ref string variableName)
        {
            bool haveVariableNameFlag = false;
            bool continueFlag = positionIndex < inputLine.Length;

            while (continueFlag)
            {
                Char c = inputLine[positionIndex];
                
                continueFlag = (Char.IsLetter(c) || c == '_');
                
                if (continueFlag)
                {
                    haveVariableNameFlag = true;
                    variableName += c;
                    positionIndex++;
                    continueFlag = positionIndex < inputLine.Length;
                }
            }
            
            return haveVariableNameFlag;
        }

        /// <summary>
        /// This function parses an operator string.
        /// </summary>
        /// <param name="inputLine">The input string to be parsed</param>
        /// <param name="positionIndex">A reference to the current parse position
        /// in the input string</param>
        /// <param name="numberString">A reference to a number string.</param>
        /// <returns>Returns the value 'true' if and only if an operator symbol is found.</returns>
        private bool GetOperator(string inputLine, ref int positionIndex)
        {
            //------------------------------------------------------------------
            // Skip whitespace characters
            //------------------------------------------------------------------
            
            SkipSpaces(inputLine, ref positionIndex);

            //------------------------------------------------------------------
            // Check for an equals sign.
            //------------------------------------------------------------------

            m_negativeOperatorFlag = false;
            bool haveEqualSignFlag = false;

            if (positionIndex < inputLine.Length)
            {
                if (inputLine[positionIndex] == '=')
                {
                    if (!m_equalSignInEquationFlag)
                    {
                        m_equalSignInEquationFlag = true;
                        haveEqualSignFlag = true;
                        positionIndex++;
                    }
                    else
                    {
                        SetLastStatusValue(LinearEquationParserStatus.ErrorMultipleEqualSigns,
                                           positionIndex);
                        return false;
                    }
                }
            }

            bool haveSignFlag = GetSign(inputLine,
                                        ref positionIndex,
                                        ref m_negativeOperatorFlag);

            return haveSignFlag || haveEqualSignFlag;
        }

        /// <summary>
        /// This method skips spaces in the input string.
        /// </summary>
        /// <param name="inputLine">The input string to be parsed</param>
        /// <param name="positionIndex">A reference to the current parse position
        /// in the input string</param>
        private void SkipSpaces(string inputLine, ref int positionIndex)
        {
            bool continueFlag = positionIndex < inputLine.Length;
            
            while (continueFlag)
            {
                char c = inputLine[positionIndex];
                
                continueFlag = Char.IsWhiteSpace(c);
                
                if (continueFlag)
                {
                    positionIndex++;
                    continueFlag = positionIndex < inputLine.Length;
                }
            }
        }

        /// <summary>
        /// This method sets the status value and saves the current parse position.
        /// </summary>
        /// <param name="status">The status value</param>
        /// <param name="positionIndex">The current parse position in the input
        /// string</param>
        private void SetLastStatusValue(LinearEquationParserStatus status,
                                        int positionIndex)
        {
            LastStatusValue = status;
            ErrorPosition = positionIndex;
        }
    }
}

 Known Issues

• The printing code is not complete.  The program can print in portrait mode, but many of the other print settings are not yet hooked up.  As I improve the printing code, I will upload the new code.
• The parser is crude, but the purpose of this program is to both to provide a simple equation solver and to provide the LinearEquationSolver class, and associated classes, for use in other applications.  I might improve the parser someday to be a more general formula parser, but for now it meets my needs. 
• The Operations/Solve menu item was made with the intent to add more features to the program.  I am conflicted as to whether a non-extensible toolbar button would be better.  I welcome ideas on this.
• The code needs more comments.  I will be improving the code and uploading the code for this article.  Other than printing, I do not expect major changes in functionality, just improvements to the code.   Check back for updates.

Points of Interest

I wrote this in 2010, originally using Visual Studio 2005.  I'm using Visual Studio 2008 now.  While the user interface (UI) is very simple for this application, I'm still struck by how easy it was to create.  The Form designer in Visual Studio made producing the UI very simple, particularly when compared to C++, whether using regular Windows programming or MFC.

History

• Initial post
• Updated the Sparse2DMatrix.cs file to remove uneeded code.  Fixed an error in the Introduction that implied semicolons can be used for input.  They cannnot be used.   Added that underscores can be used in variable names and gave an example with multi-character variable names.
• I added an image to the article.