Introduction
In data mining, Apriori is a classic algorithm for learning association rules. Apriori is designed to operate on databases containing transactions (for example, collections of items bought by customers, or details of a website frequentation).
Other algorithms are designed for finding association rules in data having no transactions (Winepi and Minepi), or having no timestamps (DNA sequencing).
Overview
The whole point of the algorithm (and data mining, in general) is to extract useful information from large amounts of data. For example, the information that a customer who purchases a keyboard also tends to buy a mouse at the same time is acquired from the association rule below:
Support: The percentage of task-relevant data transactions for which the pattern is true.
Support (Keyboard -> Mouse) = 
Confidence: The measure of certainty or trustworthiness associated with each discovered pattern.
Confidence (Keyboard -> Mouse) = 
The algorithm aims to find the rules which satisfy both a minimum support threshold and a minimum confidence threshold (Strong Rules).
- Item: article in the basket.
- Itemset: a group of items purchased together in a single transaction.
How Apriori Works
- Find all frequent itemsets:
- Get frequent items:
- Items whose occurrence in database is greater than or equal to the min.support threshold.
- Get frequent itemsets:
- Generate candidates from frequent items.
- Prune the results to find the frequent itemsets.
- Generate strong association rules from frequent itemsets
- Rules which satisfy the min.support and min.confidence threshold.
High Level Design

Low Level Design

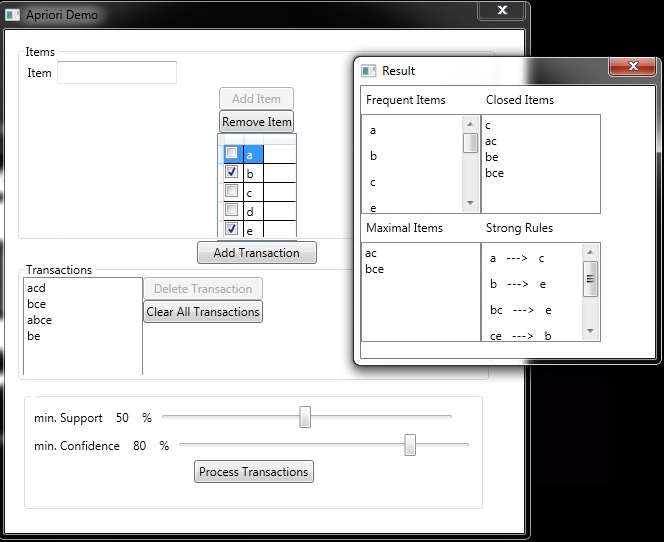
Example
A database has five transactions. Let the min sup = 50% and min con f = 80%.

Solution
Step 1: Find all Frequent Itemsets

Frequent Itemsets
{A} {B} {C} {E} {A C} {B C} {B E} {C E} {B C E}
Step 2: Generate strong association rules from the frequent itemsets

Lattice
Closed Itemset: support of all parents are not equal to the support of the itemset.
Maximal Itemset: all parents of that itemset must be infrequent.
Keep in mind:


Itemset {c} is closed as support of parents (supersets) {A C}:2, {B C}:2, {C D}:1, {C E}:2 not equal support of {c}:3.
And the same for {A C}, {B E} & {B C E}.
Itemset {A C} is maximal as all parents (supersets) {A B C}, {A C D}, {A C E} are infrequent.
And the same for {B C E}.
