Introduction
Back in 2008 when the global financial crisis was raging and the industry I worked in (Financial Services) was cutting software development costs (i.e. laying people off), I asked myself the question "What can one do to insulate themselves from the loss of their one single source of income?".
The only answers I could come up with were:
- Become so good at what I do that it would be inconceivable even in a poor job market for companies to not want to hire me.
- Build something that could work unattended and generate a second source of income.
So in an attempt to satisfy both these requirements I undertook the challenge 'build a software system that will play and win at on line poker unattended by the owner' aka PokerBot or as some might say 'a fools errand'.
Two pair, but mix with alcohol and it'll seem like a fullhouse!
Online poker seemed to me like a good arena because:
- All transactions are online and could be fully automated, meaning I don't have to take delivery of some physical commodity and worry about the related logistics.
- The participants in the market are overwhelmingly human and as we all know humans are fallable.
- The size of the market is large with many tens of thousands of players across numerous casinos.
I am not the first person to investigate or open source the code and will likely not be the last to attempt such a feat. But at the time, all the others seemed to be using C, C++ or a mixture of these with VB6. I wanted to start from scratch to help satisfy requirement 1, using C# so that if I didn't achieve requirement 2 then I could at least maintain it or reuse some or all of the code elsewhere.
Whilst I've still not achieved either 1 (it's a never ending process) or 2 (I now make more money consulting than I would do from poker), over several years I did manage to create a winning play-money bot that can execute user configurable strategies.
There have been a number of articles posted recently (Paulo Zemek 1, 2 Peter Loew) concerning evolutionary and genetic algorithmns which have rekindled my interest in a similar problem I confronted back then. As far as I know, it is one of the few applications of such an approach that you will find on codeproject that doesn't come straight from a book.
Characterising the problem
A game of Texas Hold'em has 4 distinct phases:
- Preflop - The dealer deals 2 cards to each player. The players then perform a round of betting and all survivors proceed to the next phase.
- Flop - The dealer deals 3 communal cards and again the players perform a round of betting
- Turn - 1 card is dealt communally and another round of betting occurs
- River - 1 more card is dealt communally and the final betting round occurs
Cards are dealt either privately (aka the hole) or publically as part of a communal pool (aka the board) and the position of the dealer increments after each game (aka hand).
A betting round is defined as (in order from the dealer), each player sequentially given the options:
- Fold - Exit the game and lose all the money they have staked so far
- Check - If the stake required (aka amount to Call) is zero then pass to the next player in the sequence
- Call - Bet the required amount to continue to the next phase
- Raise - Increase the stake required for all players to continue to the next phase by X amount
The betting round will continue until each non-folding player has staked an equal amount of money in that particular phase.
Once the betting round completes, all staked money is added to a communal Pot and the game continues to the next phase.
We can summisze that the action each player performs should (at the very least) depend on:
- The total money they have aka (their bank roll or stack)
- The amount they have staked so far
- The amount they need to bet in order to proceed to the next phase
- And most importantly their view of how strong their hand is.
So if we are to devise an automated 'Strategy' then it must be able to:
- Respond to events during the lifetime of the game.
- Respond differently depending on the current state of the game
- Be capable of making different strategic decisions for different game phases
- Be able to re-evaluate a decision as a game phase evolves.
This implies that we might devise a strategy that would depend on 2 degrees of freedom, the number of phases in the game (preflop, flop, turn, river) and the possible actions that a player might use (check\fold, call, raise).
From this we could create a generic strategy that involves 4x3=12 variables whose optimal values we don't yet know.
For example, imagine that the current game phase is pre-flop and we've been dealt hole cards whose relative strength we can evaluate in some way. It naturally follows that the action that our strategy should recommend should follow the pseudo code:
Case P(win) < Y0
Then Check if we can, otherwise Fold
Case Y1 > P(win) >= Y0
Then Call if our bankroll allows, otherwise Fold
Case P(win) >= Y1
Then Raise if our bankroll allows otherwise evaluate if we can call, check or fold
Where, P(win) is the probability we will win and Yn are some threshold values corresponding the actions available.
Whilst this is simplistic, this is reasonable starting point for understanding what the attached code is trying to achieve.
NB. In reality P(win) will be conditional (remember the Mont Hall problem?) on the current number of players and cards dealt, the amount we Raise should also vary and should be limited by the Kelly Criterion.
Anatomy of a Robot
Any real-time automated decisioning system will rely on 4 components:
- Datasource which continuously drives and updates...
- A representation of the current state aka Domain Model
- The Decision Engine which knows about the current state and contains a set of rules which when satisfied will then trigger...
- Actions that can be Executed either to the origin of the source or some other subsystem
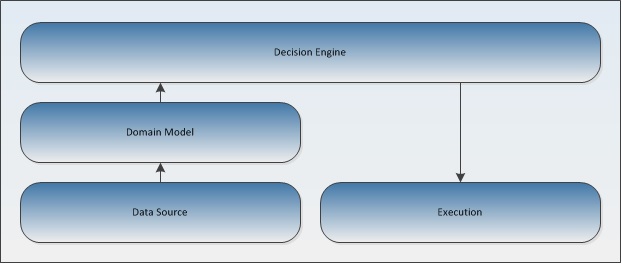
The general architecture of an automated decisioning system
Discussing datasouring and execution is beyond the scope of this article, but we will see later how the simulation mocks both.
The Domain Model
Naturally, the domain model represents the current state of the poker game. It is designed to be driven by one or more driving threads that will provide text updates to the system. As such, most of the elements of the game are based on a VisualEntity class that raises events when it's text changes. These events bubble up through the model so that an observer may register it's interest in a prticular occurance. In our case we are interested in knowing when it's our player's turn to interact with the game.
Importantly Game raises the OnInteractionRequired event, using a Memory stream to take a complete value-copy of it's current state. If we were in mutlithreaded-land it would be very important to lock access to the model and then take a snapshot of state. We don't want to be in a possition where the state we are currently making decisions on is subject to race conditions from any driving threads.
The Decision Engine
1. Orchestrator
The observer of Game events is the Orchestrator and just like a conductor in an orchestra will decide and co-ordinate the various instruments and their muscians, our Orchestrator decides which strategies to use and what subsequent actions to apply.
2. Strategies
Once the Orchestrator confirms that an event has occurred that requires it to perform an action, it then asks the current strategy what action it recommends to perform.
In this case, we have defined a base class called Strategy with an abastract method to be implemented for each particular phase of the game life cycle. Our derived MstStrategy does a number of things:
- Determines what options have been displayed to the player.
- Uses an evaluator (detailed below) to calculate it's current win probability
- Based on the win probability climbs the ladder of thresholds defined by the MeanStratifiedThreshold in order and picks out the most aggressive action it can perform.
Mean, implies that we are using the mean player expectation as a base (e.g. if their are 10 players in the game then the mean chance of winning should be 10%), for deciding if a hand is worth spending money on i.e. Callable.
A Threshold, in this case implies that in order to perform an action the expectation of winning must be above a certain value.
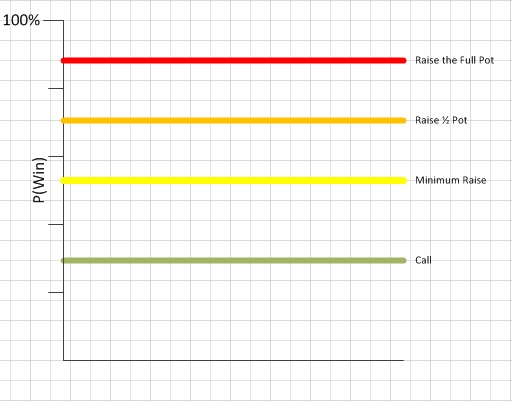
How our thresholds map to our probability of winning
For example with 5 players in total and the Callable threshold is 1.2 x the Mean
=> 1.2 x 20% = 24%
So if our win expectation is greater than 24% then the strategy will Call.
The remaining probability (i.e 100% - Mean%), is then divided equally between all other distinct options hence being Stratified. Again each threshold is a multiple of the mean +/- modifier.
In the MstStrategy we have split the raise option into Minimum raise, Half pot raise and Full raise. For the first two if they are greater than the player's stack then the Strategy should recomend a Check or Fold, but for the Full raise it recomends the player go All-In.
3. Evaluators
AllInEquity is a class that wraps a C++ implementation of an All-In Equity calculator. Derived from poker-source and the poker-eval library and originally written by James Devlin my wrapper allows the .NET user to specify their hand, the board and the number of other players in the game to calculate their expected win percentage should all players go All-In.
The BadBeat class is provided in order to check whether either the current player or an opponent has a high chance of having a straight or flush. When running in real world conditions, I often found that opponents would stay in a low staked game and achieve either of those hands on the river. To protect against this scenario BadBeat protection downgrades the suggested action to Check or Fold.
Natural Selection
We have a generic strategy which 'plays by the numbers'. It depends on the current known state of the game but is also dependent on a number of thresholds whose optimal values we don't yet know.
How can we solve this problem?
We could probably use calculus to analytically solve what probably amounts to a boundary value problem. However, we could also use a more numerical 'brute force' approach to make an approximation.
I chose the 2nd approach because my math ability is not sufficiently advanced enough to even state the equations let alone know in advance if they can be solved! Maybe the University of Alberta, Computer Poker Research Group have?
Simulating Texas Holdem
If we could simulate a poker game, fill it with robotic players (each with variants of our generic strategy), run it as fast as possible and let the robots fight it out to be the winner.
If we could also record which strategy variants won, the details of their strategy and replace losing robots with new ones (with different thresholds) then perhaps
If we ran it long enough patterns in the data might begin to emerge.
Assuming all of the above holds true then this presents us with the opportunity to calibrate the strategy and find the optimal values we would need to make the strongest pokerbot we can.
As the attached code was developed on and off between jobs and in my spare time it's state is what you might call 'the opposite of SOLID' and could certainly do with some more work to make it understandable to others. But lets assume that we only want to run it once and don't really care too much about re-use so here are the main points of interest...
The Program class and it's supporting methods simulate an ongoing game of Hold'em.
The main loop implements a never ending poker table, loading a representation of the visual state of a casino window and initialising the domain model.
It then generates 6 players, to fill the table's seats and selects a distinct strategy for each.
To make the algorithm more efficient we would like to weight the selection of new strategies such that thresholds that won before (or ones that are close to), are more likely to be used. That way useless threshold values will be discarded earlier and our simulation might more quickly 'zero in' on the optimal strategy.
I achieve this in the GetPartialPivot() function by selecting upto 3 variants who've lost the least and filling the remaining seats with some of the 'least used'.
var ranked = dc.MeanStratifiedThresholds
.Where(x => x.Used > 0 & x.Won > 0)
.OrderBy(x => x.Used - x.Won).ToArray();
MeanStratifiedThreshold[] top = null;
if (ranked.Count() >= 3)
top = ranked.Take(3).ToArray();
else if (ranked.Count() == 2)
top = ranked.Take(2).ToArray();
else if (ranked.Count() == 1)
top = ranked.Take(1).ToArray();
Each player is initialised with an observing Orchestrator and their Strategy variant, while the simulation itself observes the Orchestrator and updates the model.
The next loop in the nest simulates a poker hand until all but 1 player runs out of money. The player is declared the winner and the database is updated accordingly.
For each hand, the deck is shuffled randomly
public void Shuffle()
{
current.Clear();
Random r = new Random((int)DateTime.Now.Ticks);
while (current.Count < 52)
{
int index = r.Next(52);
var cardToInsert = cards[index];
if (!current.Contains(cardToInsert))
current.Enqueue(cardToInsert);
}
}
Cards are dequeued from the deck and dealt to players and the 2 players next to the dealer bet the Blinds.
The betting round loops until either, only one player is left in, all players are all-in or the amount left to call is zero. Each player is shown his options and a decision is triggered by setting his name to a count down (just like in a real on-line casino), before checking whether the round should complete.
var currentSeat = GetSeat(seatIndex);
if (currentSeat.HasHoleCards & 0.0M < currentSeat.Player.PLayerDetail.Stack)
{
noofPlayersNotAllIn = 0;
amountLeftToCall = FindCallValue(theGame, currentSeat);
foreach (var player in theGame.PlayersInGame)
if (player.Stack != 0.0M)
noofPlayersNotAllIn++;
if (noofPlayersNotAllIn <= 1 & amountLeftToCall <= 0.0M)
break;
ShowOptions(theGame, currentSeat);
string playerName = currentSeat.Player.Name.Text;
Console.Write(string.Format("{0}:\t", playerName));
currentSeat.Player.Name.Text = string.Format("Time {0} secs", timeTrigger);
currentSeat.Player.Name.Text = playerName;
}
Through, Preflop, Flop, Turn and River each phase is completed if enough players choose to stake money. Then at the end of the hand, for the players left in, the simulation determines the winner:
private static Seat EvaluateWinner()
{
PokerEquity.Evaluator ev = new PokerEquity.Evaluator();
string board = theGame.Hand.TableCards;
var res = new Dictionary<Seat, ulong>();
foreach(Seat s in theGame.Table.Seats.Where (x =>x.HasHoleCards))
{
ulong val = ev.Evaluate(s.HoleCards.Text, board);
res.Add(s, val);
}
var ordered = res.OrderBy( x => x.Value);
var winner = ordered.Last();
return winner.Key;
}
Before repeating the process again and again and again with the weak players dying off and the strong continuing to play...
Running the code
Once you've expanded the the zip file, PokerEvol.sln should load and compile in Visual Studio 2012 Express and greater.
Things to note:
- There is a post build event that copies Poker.Equity.dll into the run directory
- Poker.Equity.dll is a C++ library built in debug mode, so please only build your solution in the same mode.
You will also need to create a database in order to persist individual game results and store the strategy variants. Download SQL Express if you need and create a Strategy database then use the script StrategyDb_Create.sql I provide to create the tables.
Next, prime the database with initial data by running PokerEvo.exe -setup
Execute the program with no arguments and the experiment will run the simulator until you hit CTRL+C.
Here, 3 players reached the Flop but 2 felt their hands were strong enough to go all-in. Seems Player.9640 was wrong :(
Fast forward 1 week...
Over the next few hours the database will be populated with data as the simulation returns results after every game is completed. Patterns in the data will begin to emerge over time and you can stop or pause the simulation without causing a fatal issue with the experiment.
Originally I ran this for a week however if you don't want to wait a long time doing it yourself, here are my results.
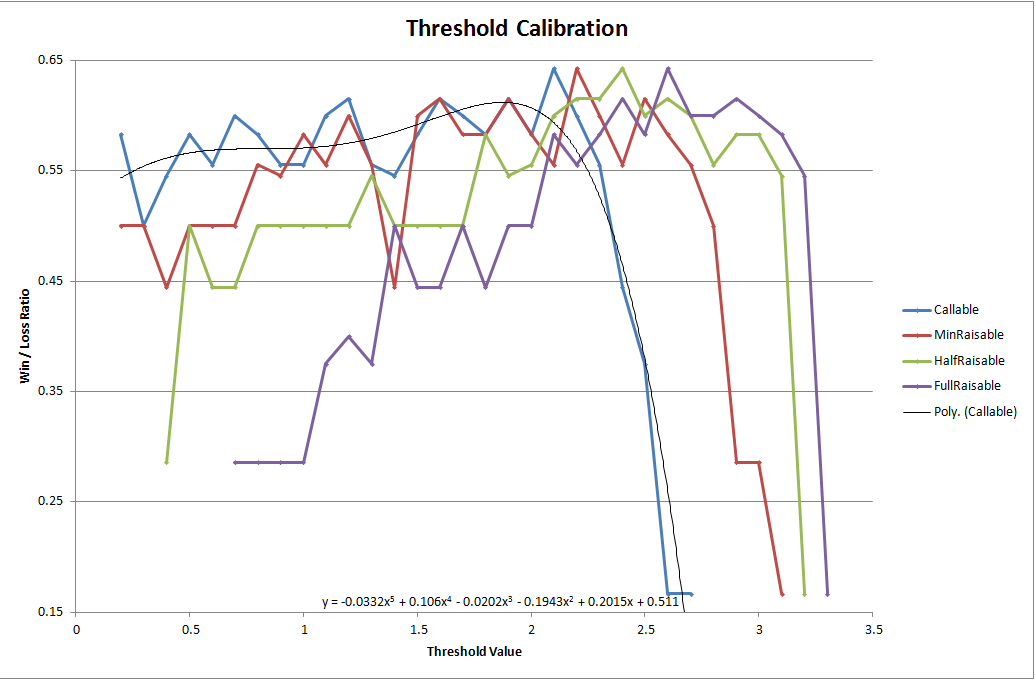
There is one marginal winner, representing the peaks of each of our plots:
| Id | Callable | MinRaisable | HalfRaisable | FullRaisable | Win/Loss Ratio | |
| 40837 | 2.1 | 2.2 | 2.4 | 2.6 | 0.642857142857143 | |
As we might have expected, as we increase each threshold value then our Win/Loss ratio gently rises to a peak before dropping off sharply. Hence, the tighter your strategy the more likely your pokerbot is to be the last man standing. However play too tightly and you'll lose your money in the ante.
Here's how I generated the graph above:
Add a View to the database with the following query:
SELECT TOP (100) PERCENT Id, Callable, FullRaisable, HalfRaisable, MinRaisable, Used, Won, CAST(Won AS float) / CAST(Used AS float) AS WinLossRatio
FROM dbo.MeanStratifiedThreshold AS m
WHERE (Used > 0) AND (Won > 0)
Then for each threshold add another View of the form:
SELECT Callable, Max(WinLossRatio)
FROM dbo.MstWinLossRatio
GROUP BY Callable
Then simply import the results into Excel and generate the plots.
Conclusions
Given a generic 'by the numbers' poker strategy, we were able to simulate a poker table long and often enough for an evolutionary process to take place. As 'less fit' strategies lost hands and money to the 'fitter' strategies they tended to die off earlier to be replaced with new variants that would also battle against the survivors.
We chose to vary our threshold values by one decimal point and within a constrained range, meaning we were able to pre-populate a table with each strategy variant. So our algorithm doesn't seem Genetic in nature, however we were able to use natural selection and weighting to mimic an evolutionary process.
As poker is a game of winner 'takes all' as well as chance then we should note that even an optimal stratagy will lose some games. Consequently the simulation needs to run long enough for us is to select the ones that have the highest win\loss percentage, but also ensure that we've given each a fair chance.
Other sources of error currently include:
- Split pots, which are not currently catered for
- Rounding differences as chips tend to be integers rather than decimals
Finally, (whilst not the aim of this article), what would happen if we used the results against real players?
Probably bad things so do NOT attempt to use! MST is just one type of strategy that could be improved upon in many ways. It does not cater for behavioral strategies encountered when playing against real players:- bluffing in particular.
Addendum
Did you run the simulation? Why not post your results below.
Did you like/hate the article? I like reading feedback and am happy to make changes so please vote and comment.
I've also been nominated for 'Best Database' article for June, so feel free to head that way and vote.
Cheers!
History
#1 Basic article and code for publication
#2 Added diagrams, pictures and reformated code examples, modified instructions as per feedback
#3 Added results and analysis of 1 week of computations including instructions
