Introduction
In 2003, Alex Fr wrote an excellent article that explains how to perform SIMD (single instruction, multiple data) processing with Intel's Streaming SIMD Extensions (SSE). SSE is a set of instructions supported by Intel processors that perform high-speed operations on large chunks of data.
In 2008, Intel introduced a new set of high-performance instructions called Advanced Vector Extensions (AVX). They perform many of the same operations as SSE instructions, but operate on larger chunks of data at higher speed. Recently, Intel has released additional instructions in the AVX2 and AVX512 sets. This article focuses on accessing AVX and AVX2 instructions through special C functions called intrinsic functions.
Instead of presenting the entire set of AVX/AVX2 intrinsics, this article focuses on math computation. In particular, the goal is to multiply complex numbers. To perform this operation with AVX/AVX2, three types of intrinsics are needed:
- Initialization intrinsics
- Arithmetic intrinsics
- Permute/shuffle intrinsics
This article discusses the intrinsics in each category and explains how they're used in code. The end of the article shows how to integrate these intrinsics to multiply complex numbers.
It's important to understand the difference between a processor instruction and an intrinsic function. An AVX instruction is an assembly command that performs an indivisible operation. For example, the AVX instruction vaddps adds two operands and places the result in a third.
To perform the operation in C/C++, the intrinsic function _mm256_add_ps() maps directly to vaddps, combining the performance of assembly with the convenience of a high-level function. An intrinsic function doesn't necessarily map to a single instruction, but AVX/AVX2 intrinsics provide reliably high performance compared to other C/C++ functions.
1. Preliminary Requirements
To understand the content of this article, you need a basic familiarity with C and SIMD processing. To execute the code, you need a CPU that supports AVX or AVX/AVX2. Here are the CPUs that support AVX:
- Intel's Sandy Bridge/Sandy Bridge E/Ivy Bridge/Ivy Bridge E
- Intel's Haswell/Haswell E/Broadwell/Broadwell E
- AMD's Bulldozer/Piledriver/Steamroller/Excavator
Every CPU that supports AVX2 also supports AVX. Here are the devices:
- Intel's Haswell/Haswell E/Broadwell/Broadwell E
- AMD's Excavator
Most of the functions discussed in this article are provided by AVX. But a few are AVX2-specific. To distinguish between them, I've preceded the names of AVX2 intrinsics with (2) in the tables throughout this article.
2. Overview of Vector Programming
AVX instructions improve an application's performance by processing large chunks of values at the same time instead of processing the values individually. These chunks of values are called vectors, and AVX vectors can contain up to 256 bits of data. Common AVX vectors contain four doubles (4 x 64 bits = 256), eight floats (8 x 32 bits = 256), or eight ints (8 x 32 bits = 256).
An example will demonstrate the power of AVX/AVX2 processing. Suppose a function needs to multiply eight floats of one array by eight floats of a second array and add the result to a third array. Without vectors, the function might look like this:
multiply_and_add(const float* a, const float* b, const float* c, float* d) {
for(int i=0; i<8; i++) {
d[i] = a[i] * b[i];
d[i] = d[i] + c[i];
}
}
Here's what the function looks like with AVX2:
__m256 multiply_and_add(__m256 a, __m256 b, __m256 c) {
return _mm256_fmadd_ps(a, b, c);
}
This AVX2 intrinsic function _mm256_fmadd_ps processes twenty-four floats, but it doesn't map to a single instruction. Instead, it executes three instructions: vfmadd132ps, vfmadd213ps, and vfmadd231ps. Despite this, it executes quickly and it's much faster than looping through the individual elements.
Despite the power of Intel's intrinsics, they make many programmers nervous. This is usually for two reasons. First, the data types have strange names like __m256. Second, the functions have strange names like _mm256_fmadd_ps. Therefore, before I discuss the intrinsic functions in detail, I want to discuss Intel's data types and naming conventions.
3. Fundamentals of AVX Programming
Most of this article focuses on the math-related intrinsic functions provided by AVX and AVX2. But before looking at the functions, it's important to understand three points:
- Data types
- Function naming conventions
- Compiling AVX applications
This section touches on each of these points and provides a simple application that subtracts one vector from another.
3.1 Data Types
A few intrinsics accept traditional data types like ints or floats, but most operate on data types that are specific to AVX and AVX2. There are six main vector types and Table 1 lists each of them.
Table 1: AVX/AVX2 Data Types
| Data Type | Description |
__m128 | 128-bit vector containing 4 floats |
__m128d | 128-bit vector containing 2 doubles |
__m128i | 128-bit vector containing integers |
__m256 | 256-bit vector containing 8 floats |
__m256d | 256-bit vector containing 4 doubles |
__m256i | 256-bit vector containing integers |
Each type starts with two underscores, an m, and the width of the vector in bits. AVX512 supports 512-bit vector types that start with _m512, but AVX/AVX2 vectors don't go beyond 256 bits.
If a vector type ends in d, it contains doubles, and if it doesn't have a suffix, it contains floats. It might look like _m128i and _m256i vectors must contain ints, but this isn't the case. An integer vector type can contain any type of integer, from chars to shorts to unsigned long longs. That is, an _m256i may contain 32 chars, 16 shorts, 8 ints, or 4 longs. These integers can be signed or unsigned.
3.2 Function Naming Conventions
The names of AVX/AVX2 intrinsics can be confusing at first, but the naming convention is really straightforward. Once you understand it, you'll be able to judge approximately what a function does by looking at its name. A generic AVX/AVX2 intrinsic function is given as follows:
_mm<bit_width>_<name>_<data_type>
The parts of this format are given as follows:
<bit_width> identifies the size of the vector returned by the function. For 128-bit vectors, this is empty. For 256-bit vectors, this is set to 256.<name> describes the operation performed by the intrinsic<data_type> identifies the data type of the function's primary arguments
This last part, <data_type>, is a little complicated. It identifies the content of the input values, and can be set to any of the following values:
ps - vectors contain floats (ps stands for packed single-precision)pd - vectors contain doubles (pd stands for packed double-precision)epi8/epi16/epi32/epi64 - vectors contain 8-bit/16-bit/32-bit/64-bit signed integersepu8/epu16/epu32/epu64 - vectors contain 8-bit/16-bit/32-bit/64-bit unsigned integerssi128/si256 - unspecified 128-bit vector or 256-bit vectorm128/m128i/m128d/m256/m256i/m256d - identifies input vector types when they're different than the type of the returned vector
As an example, consider _mm256_srlv_epi64. Even if you don't know what srlv means, the _mm256 prefix tells you the function returns a 256-bit vector and the _epi64 tells you that the arguments contain 64-bit signed integers.
As a second example, consider _mm_testnzc_ps. The _mm implies that the function returns a 128-bit vector. The _ps at the end implies that the argument vectors contain floats.
AVX data types start with two underscores and an m. Functions start with an underscore and two ms. I tend to get this confused, so I came up with a way to remember the difference: a data type represents memory and a function represents a multimedia operation. That's the best I can do.
3.3 Building AVX Applications
To build an application that uses AVX intrinsics, you don't need to link any libraries. But you need to include the immintrin.h header file. This header includes other headers that map AVX/AVX2 functions to instructions.
The code in hello_avx.c shows what a basic AVX application looks like:
#include <immintrin.h>
#include <stdio.h>
int main() {
__m256 evens = _mm256_set_ps(2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0);
__m256 odds = _mm256_set_ps(1.0, 3.0, 5.0, 7.0, 9.0, 11.0, 13.0, 15.0);
__m256 result = _mm256_sub_ps(evens, odds);
float* f = (float*)&result;
printf("%f %f %f %f %f %f %f %f\n",
f[0], f[1], f[2], f[3], f[4], f[5], f[6], f[7]);
return 0;
}
To build the application, you need to tell the compiler that the architecture supports AVX. The flag depends on the compiler, and gcc requires the -mavx flag. Therefore, the hello_avx.c source file can be compiled with the following command:
gcc -mavx -o hello_avx hello_avx.c
In this example, all the functions start with _mm256 and end with _ps, so I hope it's clear that all the operations involve 256-bit vectors containing floats. I also hope it's clear that each element in the resulting vector equals 1.0. If you run the application, you'll see that this is the case.
4. Initialization Intrinsics
Before you can operate on AVX vectors, you need to fill the vectors with data. Therefore, the first set of intrinsics discussed in this article initialize vectors with data. There are two ways of doing this: initializing vectors with scalar values and initializing vectors with data loaded from memory.
4.1 Initialization with Scalar Values
AVX provides intrinsic functions that combine one or more values into a 256-bit vector. Table 2 lists their names and provides a description of each.
There are similar intrinsics that initialize 128-bit vectors, but those are provided by SSE, not AVX. The only difference in the functions' names is that _mm256_ is replaced with _mm_.
Table 2: Initialization Intrinsics
| Function | Description |
_mm256_setzero_ps/pd | Returns a floating-point vector filled with zeros |
_mm256_setzero_si256 | Returns an integer vector whose bytes
are set to zero |
_mm256_set1_ps/pd | Fill a vector with a floating-point value |
_mm256_set1_epi8/epi16
_mm256_set1_epi32/epi64 | Fill a vector with an integer |
_mm256_set_ps/pd | Initialize a vector with eight floats (ps)
or four doubles (pd)
|
| _mm256_set_epi8/epi16
_mm256_set_epi32/epi64
| Initialize a vector with integers |
_mm256_set_m128/m128d/
_mm256_set_m128i | Initialize a 256-bit vector with
two 128-bit vectors
|
_mm256_setr_ps/pd | Initialize a vector with eight floats (ps)
or four doubles (pd) in reverse order |
_mm256_setr_epi8/epi16
_mm256_setr_epi32/epi64 | Initialize a vector with integers in reverse order |
The first functions in the table are the easiest to understand. _m256_setzero_ps returns an __m256 vector containing eight floats set to zero. Similarly, _m256_setzero_si256 returns an __m256i vector whose bytes are set to zero. As an example, the following line of code creates a 256-bit vector that contains four doubles set to zero:
_m256d dbl_vector = _m256_setzero_pd();
The functions whose names contain set1 accept a single value and repeat it throughout the vector. For example, the following line of code creates an __m256i whose sixteen short values are set to 47:
_m256i short_vector = _m256_set1_pd();
The rest of the functions in Table 2 contain _set_ or _setr_. These functions accept a series of values, one for each element of the vector. These values are placed in the returned vector, and the order important to understand. The following function call returns a vector containing eight ints whose values range from 1 to 8:
_m256i int_vector = _m256_set_epi32(1, 2, 3, 4, 5, 6, 7, 8);
You might expect the values to be stored in the order in which they're given. But Intel's architecture is little-endian, so the least-significant value (8), is stored first and the most-significant value (1) is stored last.
You can verify this by casting int_vector to an int pointer and printing the stored values. This is shown with the following code:
__m256i int_vector = _mm256_set_epi32(1, 2, 3, 4, 5, 6, 7, 8);
int *ptr = (int*)&int_vector;
printf("%d %d %d %d %d %d %d %d\n", ptr[0], ptr[1], ptr[2], ptr[3], ptr[4], ptr[5], ptr[6], ptr[7]);
--> 8 7 6 5 4 3 2 1
If you want the values to be stored in the given order, you can create vectors with one of the _setr_ functions, where r presumably stands for reverse. The following code shows how this works:
__m256i int_vector = _mm256_setr_epi32(1, 2, 3, 4, 5, 6, 7, 8);
int *ptr = (int*)&int_vector;
printf("%d %d %d %d %d %d %d %d\n", ptr[0], ptr[1], ptr[2], ptr[3], ptr[4], ptr[5], ptr[6], ptr[7]);
--> 1 2 3 4 5 6 7 8
It's interesting to note that neither AVX nor AVX2 provide intrinsics that initialize vectors with unsigned integers. However, they provide functions that operate on vectors with unsigned integers.
4.2 Loading Data from Memory
A common usage of AVX/AVX2 is to load data from memory into vectors, process the vectors, and store the results back to memory. The first step is accomplished with the intrinsic functions listed in Table 3. The last two functions are preceded with (2) because they're provided by AVX2, not AVX.
Table 3: Vector Load Intrinsics
| Data Type | Description |
_mm256_load_ps/pd | Loads a floating-point vector from an
aligned memory address |
_mm256_load_si256 | Loads an integer vector from an aligned
memory address |
_mm256_loadu_ps/pd | Loads a floating-point vector from an
unaligned memory address |
_mm256_loadu_si256 | Loads an integer vector from an unaligned
memory address |
_mm_maskload_ps/pd
_mm256_maskload_ps/pd | Load portions of a 128-bit/256-bit
floating-point vector according to a mask |
(2)_mm_maskload_epi32/64
(2)_mm256_maskload_epi32/64 | Load portions of a 128-bit/256-bit
integer vector according to a mask |
When loading data into vectors, memory alignment becomes particularly important. Each _mm256_load_* intrinsic accepts a memory address that must be aligned on a 32-byte boundary. That is, the address must be divisible by 32. The following code shows how this can be used in practice:
float* aligned_floats = (float*)aligned_alloc(32, 64 * sizeof(float));
... Initialize data ...
__m256 vec = _mm256_load_ps(aligned_floats);
Any attempt to load unaligned data with _m256_load_* produces a segmentation fault. If the data isn't aligned at a 32-bit boundary, the _m256_loadu_* functions should be used instead. This is shown with the following code:
float* unaligned_floats = (float*)malloc(64 * sizeof(float));
... Initialize data ...
__m256 vec = _mm256_loadu_ps(unaligned_floats);
Suppose you want to process a float array using AVX vectors, but the length of the array is 11, which isn't divisible by 8. In this case, the last five floats of the second __m256 vector need to be set to zero so they don't affect the computation. This selective loading can be accomplished with the _maskload_ functions at the bottom of Table 3.
Each _maskload_ function accepts two arguments: a memory address and an integer vector with the same number of elements as the returned vector. For each element in the integer vector whose highest bit is one, the corresponding element in the returned vector is read from memory. If the highest bit in the integer vector is zero, the corresponding element in the returned vector is set to zero.
An example will clarify how these functions are used. The code in mask_load.c reads eight ints into a vector, and the last three should be set to zero. The function to use is _mm256_maskload_epi32, and its second argument should be a __m256i mask vector. This mask vector contains five ints whose highest bit equals 1 and three ints whose highest bit is zero. Here's what the code looks like:
#include <immintrin.h>
#include <stdio.h>
int main() {
int i;
int int_array[8] = {100, 200, 300, 400, 500, 600, 700, 800};
__m256i mask = _mm256_setr_epi32(-20, -72, -48, -9, -100, 3, 5, 8);
__m256i result = _mm256_maskload_epi32(int_array, mask);
int* res = (int*)&result;
printf("%d %d %d %d %d %d %d %d\n",
res[0], res[1], res[2], res[3], res[4], res[5], res[6], res[7]);
return 0;
}
If you run this application on a system that supports AVX2, it will print the following result:
100 200 300 400 500 0 0 0
There are three points I'd like to mention:
- The code sets the mask vector's content with a
_setr_ function instead of _set_ because it orders the vector's elements as they're delivered to the function. - The highest bit of a negative integer is always 1. This is why the mask vector contains five negative numbers and three positive numbers.
- The
_mm256_maskload_epi32 function is provided by AVX2, not AVX. Therefore, to compile this code with gcc, the -mavx2 flag must be used instead of -mavx.
In addition to the functions listed in Table 3, AVX2 provides gather functions that load indexed data from memory.
5. Arithmetic Intrinsics
Math is the primary reason for AVX's existence, and the fundamental operations are addition, subtraction, multiplication, and division. This section presents the intrinsics that perform these operations, and also looks at the new fused multiply-and-add functions provided by AVX2.
5.1 Addition and Subtraction
Table 4 lists the AVX/AVX2 intrinsics that perform addition and subtraction. Most of them operate on vectors containing integers because of the concern with saturation.
Table 4: Addition and Subtraction Intrinsics
| Data Type | Description |
_mm256_add_ps/pd | Add two floating-point vectors |
_mm256_sub_ps/pd | Subtract two floating-point vectors |
(2)_mm256_add_epi8/16/32/64 | Add two integer vectors |
(2)_mm236_sub_epi8/16/32/64 | Subtract two integer vectors |
(2)_mm256_adds_epi8/16
(2)_mm256_adds_epu8/16 | Add two integer vectors with saturation |
(2)_mm256_subs_epi8/16
(2)_mm256_subs_epu8/16 | Subtract two integer vectors with saturation
|
_mm256_hadd_ps/pd | Add two floating-point vectors horizontally |
_mm256_hsub_ps/pd | Subtract two floating-point vectors horizontally |
(2)_mm256_hadd_epi16/32 | Add two integer vectors horizontally |
(2)_mm256_hsub_epi16/32 | Subtract two integer vectors horizontally |
(2)_mm256_hadds_epi16 | Add two vectors containing shorts horizontally with saturation |
(2)_mm256_hsubs_epi16 | Subtract two vectors containing shorts horizontally with saturation |
_mm256_addsub_ps/pd | Add and subtract two floating-point vectors |
When adding or subtracting integer vectors, it's important to see the difference between the _add_/_sub_ functions and the _adds_/_subs_ functions. The extra s stands for saturation, which is produced when the result requires more memory than the vector can store. Functions that take saturation into account clamp the result to the minimum/maximum value that can be stored. Functions without saturation ignore the memory issue when saturation occurs.
For example, suppose a vector contains signed bytes, so the maximum value for each element is 127 (0x7F). If an operation adds 98 to 85, the mathematical sum is 183 (0xB7).
- If the values are added with
_mm256_add_epi8, the saturation will be ignored and the stored result will be -73 (0xB7). - If the values are added with
_mm256_adds_epi8, the result will be clamped to the maximum value, 127 (0x7F).
As another example, consider two vectors that contain signed short integers. The minimum value is -32,768. If you compute -18,000 - 19,000, the mathematical result is -37,000 (0xFFFF6F78 as a 32-bit integer).
- If the values are subtracted with
_mm256_sub_epi16, the saturation will be ignored and the stored result will be 28,536 (0x6F78). - If the values are subtracted with
_mm256_subs_epi16, the result will be clamped to the minimum value, -32,768 (0x8000).
The _hadd_/_hsub_ functions perform addition and subtraction horizontally. That is, instead of adding or subtracting elements of different vectors, they add or subtract adjacent elements within each vector. The results are stored in an interleaved fashion. Figure 1 shows how this works for _mm256_hadd_pd, which horizontally adds double vectors A and B:
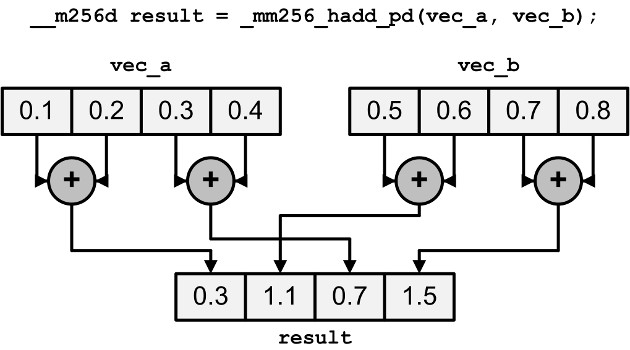
Figure 1: Horizontal Addition of Two Vectors
This may seem strange to add and subtract elements horizontally, but these operations are helpful when multiplying complex numbers. This is explained later in this article.
The last function in Table 4, _mm256_addsub_ps/pd, alternately subtracts and adds elements of two floating-point vectors. That is, even elements are subtracted and odd elements are added. For example, if vec_a contains (0.1, 0.2, 0.3, 0.4) and vec_b contains (0.5, 0.6, 0.7, 0.8), _mm256_addsub_pd(vec_a, vec_b) equals (-0.4, 0.8, -0.4, 1.2).
5.2 Multiplication and Division
Table 5 lists the AVX/AVX2 intrinsics that perform multiplication and division. As with addition and subtraction, there are special intrinsics for operating on integers.
Table 5: Multiplication and Division Intrinsics
| Data Type | Description |
_mm256_mul_ps/pd | Multiply two floating-point vectors |
(2)_mm256_mul_epi32/
(2)_mm256_mul_epu32 | Multiply the lowest four elements of vectors containing 32-bit integers |
(2)_mm256_mullo_epi16/32 | Multiply integers and store low halves |
(2)_mm256_mulhi_epi16/
(2)_mm256_mulhi_epu16 | Multiply integers and store high halves
|
(2)_mm256_mulhrs_epi16 | Multiply 16-bit elements to form 32-bit elements |
_mm256_div_ps/pd | Divide two floating-point vectors |
If two N-bit numbers are multiplied on a computer, the result can take up 2N bits. For this reason, only the four low elements of the _mm256_mul_epi32 and _mm256_mul_epu32 intrinsics are multiplied together, and the result is a vector containing four long integers. Figure 2 shows how this works:

Figure 2: Multiplying Low Elements of Integer Vectors
The _mullo_ functions are similar to the integer _mul_ functions, but instead of multiplying low elements, they multiply every element of both vectors store only the low half of each product. Figure 3 shows what this looks like:
Figure 3: Multiplying Integers and Storing Low Halves
The _mm256_mulhi_epi16 and _mm256_mulhi_epu16 intrinsics are similar, but they store the high halves of the integer products.
5.3 Fused Multiply and Add (FMA)
As mentioned earlier, the result of multiplying two N-bit numbers can occupy 2N bits. Therefore, when you multiply two floating-point values, a and b, the result is really round(a * b), where round(x) returns the floating-point value closest to x. This loss of accuracy increases as further operations are performed.
AVX2 provides instructions that fuse multiplication and addition together. That is, instead of returning round(round(a * b) + c), they return round(a * b + c). As a result, these instructions provide greater speed and accuracy than performing multiplication and addition separately.
Table 6 lists the FMA intrinsics provided by AVX2 and includes a description of each. Every instruction in the table accepts three input vectors, and I've referred to them as a, b, and c.
Table 6: FMA Intrinsics
| Data Type | Description |
(2)_mm_fmadd_ps/pd/
(2)_mm256_fmadd_ps/pd | Multiply two vectors and add the product to a third (res = a * b + c) |
(2)_mm_fmsub_ps/pd/
(2)_mm256_fmsub_ps/pd | Multiply two vectors and subtract a vector from the product (res = a * b - c)
|
(2)_mm_fmadd_ss/sd | Multiply and add the lowest element in the vectors (res[0] = a[0] * b[0] + c[0]) |
(2)_mm_fmsub_ss/sd | Multiply and subtract the lowest element in the vectors (res[0] = a[0] * b[0] - c[0]) |
(2)_mm_fnmadd_ps/pd
(2)_mm256_fnmadd_ps/pd | Multiply two vectors and add the negated product to a third (res = -(a * b) + c)
|
(2)_mm_fnmsub_ps/pd/
(2)_mm256_fnmsub_ps/pd | Multiply two vectors and add the negated product to a third (res = -(a * b) - c) |
(2)_mm_fnmadd_ss/sd | Multiply the two lowest elements and add the negated product to the lowest element of the third vector (res[0] = -(a[0] * b[0]) + c[0]) |
(2)_mm_fnmsub_ss/sd | Multiply the lowest elements and subtract the lowest element of the third vector from the negated product (res[0] = -(a[0] * b[0]) - c[0]) |
(2)_mm_fmaddsub_ps/pd/
(2)_mm256_fmaddsub_ps/pd | Multiply two vectors and alternately add and subtract from the product (res = a * b - c) |
(2)_mm_fmsubadd_ps/pd/
(2)_mmf256_fmsubadd_ps/pd | Multiply two vectors and alternately subtract and add from the product (res = a * b - c) |
If an intrinsic's name ends with _ps or _pd, every element of the input vectors is included in the operation. If an intrinsic's name ends with _ss or _sd, only the lowest element is included. The rest of the elements in the output vector are set equal to the elements of the first input vector. For example, suppose vec_a = (1.0, 2.0), vec_b = (5.0, 10.0), and vec_c = (7.0, 14.0). In this case, _mm_fmadd_sd(vec_a, vec_b, vec_c) returns (12.0, 2.0) because (1.0 * 5.0) + 7.0 = 12.0 and 2.0 is the second element of vec_a.
It's important to see the difference between the _fmadd_/_fmsub_ and _fnmadd_/_fnmsub_ intrinsics. The latter functions negate the product of the first two input vectors before adding or subtracting the third input vector.
The _fmaddsub_ and _fmsubadd_ intrinsics alternate between adding and subtracting elements of the third vector. The _fmaddsub_ intrinsics add odd elements and subtract even elements. The _fmsubadd_ intrinsics subtract odd elements and add even elements. The code in fmatest.c shows how the _mm256_fmaddsub_pd intrinsic can be used in practice.
#include <immintrin.h>
#include <stdio.h>
int main() {
__m256d veca = _mm256_setr_pd(6.0, 6.0, 6.0, 6.0);
__m256d vecb = _mm256_setr_pd(2.0, 2.0, 2.0, 2.0);
__m256d vecc = _mm256_setr_pd(7.0, 7.0, 7.0, 7.0);
__m256d result = _mm256_fmaddsub_pd(veca, vecb, vecc);
double* res = (double*)&result;
printf("%lf %lf %lf %lf\n", res[0], res[1], res[2], res[3]);
return 0;
}
When this code is compiled and executed on a processor that supports AVX2, the printed results are as follows:
5.000000 19.000000 5.000000 19.000000
The FMA instructions are provided by AVX2, so you might think the -mavx2 flag is needed for building the application with gcc. But I've found that the -mfma flag is required instead. Otherwise, I get strange compile errors.
6. Permuting and Shuffling
Many applications must rearrange vector elements to ensure that operations are performed properly. AVX/AVX2 provides a number of intrinsic functions for this purpose, and two major categories are the _permute_ functions and the _shuffle_ functions. This section presents both types of intrinsics.
6.1 Permuting
AVX provides functions that return a vector containing the rearranged elements of a vector. Table 7 lists these permute functions and provides a description of each.
Table 7: Permute Intrinsics
| Data Type | Description |
_mm_permute_ps/pd/
_mm256_permute_ps/pd | Select elements from the input vector based on an 8-bit control value |
(2)_mm256_permute4x64_pd/
(2)_mm256_permute4x64_epi64 | Select 64-bit elements from the input vector based on an 8-bit control value |
_mm256_permute2f128_ps/pd | Select 128-bit chunks from two input vectors based on an 8-bit control value
|
_mm256_permute2f128_si256 | Select 128-bit chunks from two input vectors based on an 8-bit control value |
_mm_permutevar_ps/pd
_mm256_permutevar_ps/pd | Select elements from the input vector based on bits in an integer vector
|
(2)_mm256_permutevar8x32_ps/
(2)_mm256_permutevar8x32_epi32 | Select 32-bit elements (floats and ints) using indices in an integer vector |
The _permute_ intrinsics accept two arguments: an input vector and an 8-bit control value. The bits of the control value determine which of the input vector's elements is inserted into the output. For _mm256_permute_ps, each pair of control bits determines an upper and lower output element by selecting one of the upper or lower elements in the input vector. This is complicated, so I hope Figure 4 will make the operation a little clearer:

Figure 4: Operation of the Permute Intrinsic Function
As shown in the figure, values of the input vector may be repeated multiple times in the output. Other input values may not be selected at all.
In _mm256_permute_pd, the low four bits of the control value select between adjacent pairs of doubles. _mm256_permute4x4_pd is similar, but uses all of the control bits to select which 64-bit element is placed in the output. In the _permute2f128_ intrinsics, the control value selects 128-bit chunks from the two input vectors instead of selecting elements from one input vector.
The _permutevar_ intrinsics perform the same operation as the _permute_ intrinsics. But instead of using 8-bit control values to select elements, they rely on integer vectors with the same size as the input vector. For example, the input vector of _mm256_permute_ps is a _mm256, so the integer vector is an _mm256i. The high bits of the integer vector perform selection in the same way as the bits of the 8-bit control values of the _permute_ intrinsics.
6.2 Shuffling
Like the _permute_ intrinsics, the _shuffle_ intrinsics select elements from one or two input vectors and place them in the output vector. Table 8 lists the functions and provides a description of each.
Table 8: Shuffle Intrinsics
| Data Type | Description |
_mm256_shuffle_ps/pd | Select floating-point elements according to an 8-bit value
|
_mm256_shuffle_epi8/
_mm256_shuffle_epi32 | Select integer elements according to an
8-bit value |
(2)_mm256_shufflelo_epi16/
(2)_mm256_shufflehi_epi16 | Select 128-bit chunks from two input vectors based on an 8-bit control value
|
All _shuffle_ intrinsics operate on 256-bit vectors. In each case, the last argument is an 8-bit value that determines which input elements should be placed in the output vector.
For _mm256_shuffle_ps, only the high four bits of the control value are used. If the input vectors contain ints or floats, all the control bits are used. For _mm256_shuffle_ps, the first two pairs of bits select elements from the first vector and the second two pairs of bits select elements from the second vector. Figure 5 illustrates how this works:

Figure 5: Operation of the Shuffle Intrinsic Function
To shuffle 16-bit values, AVX2 provides _mm256_shufflelo_epi16 and _mm256_shufflehi_epi16. As with _mm256_shuffle_ps, the control value is split into four pairs of bits that select from eight elements. But for _mm256_shufflelo_epi16, the eight elements are taken from the eight low 16-bit values. For _mm256_shufflehi_epi16, the eight elements are taken from the eight high 16-bit values.
7. Complex Multiplication
Complex multiplication is a time-consuming operation that must be performed repeatedly in signal processing applications. I won't go deeply into the theory, but every complex number can be expressed as a + bi, where a and b are floating-point values and i is the square-root of -1. a is called the real part and b is called the imaginary part. If (a + bi) and (c + di) are multiplied, the product equals (ac - bd) + (ad + bc)i.
Complex numbers can be stored in interleaved fashion, which means each real part is followed by the imaginary part. Suppose vec1 is a __m256d that stores two complex numbers, (a + bi) and (x + yi), and vec2 is a __m256d that stores (c + di) and (z + wi). Figure 6 illustrates how the values are stored. As shown, the prod vector stores the two products: (ac - bd) + (ad + bc)i and (xz - yw) + (xw + yz)i.

Figure 6: Complex Multiplication Using Vectors
I don't know the fastest way to compute complex products with AVX/AVX2. But I've devised a method that has given me good results. It consists of five steps:
- Multiply
vec1 and vec2 and store the result in vec3. - Switch the real/imaginary values of
vec2. - Negate the imaginary values of
vec2. - Multiply
vec1 and vec2 and store the result in vec4. - Use horizontal subtraction on
vec3 and vec4 to produce the answer in vec1.
The code in complex_mult.c shows how this can be performed using AVX intrinsics:
#include <immintrin.h>
#include <stdio.h>
int main() {
__m256d vec1 = _mm256_setr_pd(4.0, 5.0, 13.0, 6.0);
__m256d vec2 = _mm256_setr_pd(9.0, 3.0, 6.0, 7.0);
__m256d neg = _mm256_setr_pd(1.0, -1.0, 1.0, -1.0);
__m256d vec3 = _mm256_mul_pd(vec1, vec2);
vec2 = _mm256_permute_pd(vec2, 0x5);
vec2 = _mm256_mul_pd(vec2, neg);
__m256d vec4 = _mm256_mul_pd(vec1, vec2);
vec1 = _mm256_hsub_pd(vec3, vec4);
double* res = (double*)&vec1;
printf("%lf %lf %lf %lf\n", res[0], res[1], res[2], res[3]);
return 0;
}
This code operates on double vectors, but the method can easily be extended to support float vectors.
Using the Code
The AVX_examples.zip archive contains the four source files mentioned in this article. I haven't provided any makefiles, but the code can be compiled with the following commands:
gcc -mavx -o hello_avx hello_avx.cgcc -mavx2 -o mask_load mask_load.cgcc -mfma -o fmatest fmatest.cgcc -mavx -o complex_mult complex_mult.c
Of course, the applications will only execute properly if the processor supports AVX or AVX/AVX2.
Points of Interest
Many developers may avoid learning AVX/AVX2 in the hope that the compiler will perform autovectorization. Autovectorization is a great feature, but if you understand the intrinsics, you can rearrange your algorithm to take better advantage of SIMD processing. By inserting AVX/AVX2 intrinsics, I have dramatically improved the processing speed of my signal processing applications.
History
2/20 - Fixed formatting and image links
4/2 - Fixed a couple typographical errors
