Introduction
This information will allow you to determine the direction that an object ("Chaser") must move so that it is able to intercept a target object ("Runner"). It assumes that you know the positions of both objects in 2D space. It assumes that you know the speed at which your Chaser can move. It assumes that you know the current speed and direction of the Runner.
Both the Chaser and the Runner are abstracted to points on a plane. This suffices for many simulation and video game scenarios. The collision between the game objects will occur slightly earlier than this algorithm predicts if the game objects' bounding volume is used for collision detection.
Background
In most video games, it suffices to approximate real-world physical phenomena. For instance, since computers operate in a discrete manner (one instruction after another), what happens in the time between instructions must be approximated for a great many things. Sometimes games work better by skipping the physics altogether, simply allowing an object's speed to instantly change from 0 to maxSpeed without any interest in the physics of force and inertia. This suspension of physics is perfect for many games- Imagine if PacMan had to slow down every time he made a turn.
In this article, I'll describe a process for finding an interception point assuming that inertia and acceleration are being approximated or ignored, and that the game can re-compute this interception point regularly (every game frame if needed). The algorithm is 100% accurate (not an approximation) if our game can put physics aside, allowing the direction and speed of the Chaser to be set instantly (no acceleration over time).
There is an article here that gives a very thorough methodology for doing a similar thing. I was interested in a much simpler approach, useful in video games.
This approach makes heavy use of vectors, described in great detail in many other articles. I will provide the basis needed to understand how 2D vectors are used within the framework of this article.
The code is implemented in C#, but (hopefully) easily translated to other languages.
Some 2D Vector Math
Note- I acknowledge here that vectors have many different uses, can represent many different things, can be expressed in many different forms, yadda yadda yadda. I would like to streamline this text by omitting further acknowledgement of all the possible different ways Vectors can be used or implemented.
Since this article relies heavily on simple 2-dimensional vectors, I will review the topic and provide clarification on the notations used herein. A vector in two dimensions will be composed of two elements- x and y. These are real numbers, but will be represented by floating-point values when used in the included software.
A Scalar is a quantity that only has magnitude, not direction. Scalar values are represented typically by primitive types- int's, float's, etc. A scalar is "just a number"- nothing special about it. I will use double-precision floating point numbers to represent scalars.
A Vector is a quantity that has both direction and magnitude. By performing operations on the x and y elements of a vector, one can derive both the vector's direction and its magnitude. X and y are scalar values that together make up a vector. It is important to note that the semantics of x and y assume a Cartesian coordinate system. It is every bit as viable to use a polar coordinate system where one element represents length and the other element represents direction. I will derive polar coordinates from the stored Cartesian coordinates.
Vectors will be represented with capitalized and bolded variables (e.g. V). Scalars will be represented with lowercase bolded variables (e.g. s). The x and y components of vector V will be denoted by V.x and V.y.
Vectors can be of two semantic types- Position (Point) Vectors and Velocity Vectors. Both are represented identically, as a pair of values x and y. A Position Vector represents a vector from the origin (0,0) to a point on the plane. This corresponds directly to the basic understanding of a position having (x,y) coordinates.
A Velocity Vector represents a direction and a speed. It is not located at any "place" on a 2D plane. It can, however, represent the difference between two point vectors quite easily. A Velocity Vector represents how far, and in what direction, a Point will move in one unit of time. The magnitude of a Velocity Vector represents the speed component of the velocity. A Velocity Vector's unit vector represents the direction component of the velocity.
The only difference between a 2D Velocity Vector and a 2D Position Vector is semantic. How one uses the vector determines what it is. This is contrasted with the notion that a vector has some intrinsic identifying feature which determines if it is a Position or a Velocity vector. It does not.
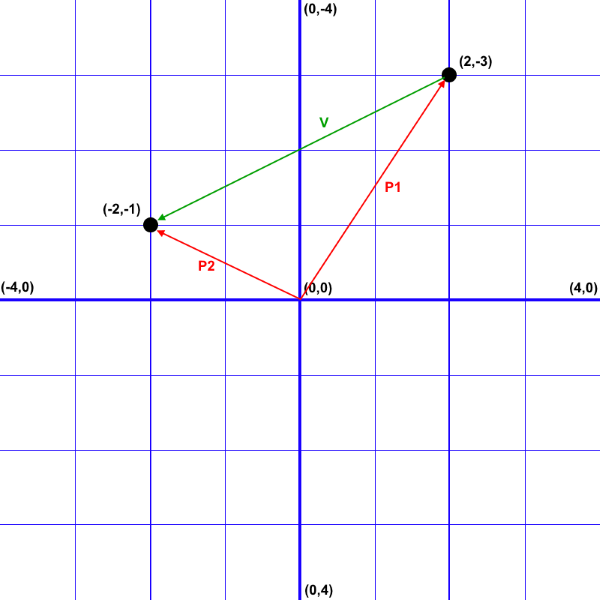
This graphic shows two Position Vectors P1 and P2 along with a Velocity Vector V. An English Language translation of this picture: If a game object is at point P1, and it is moving with velocity V, and one unit of time passes, the game object will be at point P2.

In the picture, P1 has value (2,-3) and P2 has value (-2,-1). V has value (-4,2). Also, V = P2 - P1. This is read as the vector from P1 to P2. The ordering of these two terms is important. Also note that it may feel "backward" to some people that the "to" point gets the "from" point subtracted from it.
Vectors have many similar arithmetic operations to scalars, and most of them are intuitive. I'll show the ones used in this algorithm:
| Operation | Notation | Algorithm |
| Addition | R = P + Q | $R.x = P.x + Q.x$
$R.y = P.y + Q.y$
|
| Subtraction | R = P - Q | $R.x = P.x - Q.x$
$R.y = P.y - Q.y$
|
| Scalar Multiplication | R = cP | $R.x = cP.x$
$R.y = cP.y$
|
| Magnitude ("Length")
| m = |P| | $m=\sqrt{P.x^2 + P.y^2}$
|
| Normal ("Unit Vector") | R = normalize(P) | $R=\frac{1}{|P|}P$
|
| Dot Product | dot = P · Q | $P\cdot Q = P.xQ.x + P.yQ.y$
|
The first three operations (Addition, Subtraction, and Scalar Multiplication) are straight-forward. I won't discuss them here.
The magnitude operation represents the length of a vector. The formula is identical to the formula for determining the Euclidean distance between two points. The magnitude of a Velocity Vector is the speed component of the velocity. The magnitude of a Position Vector is how far away from the origin the point is. The magnitude of the difference between two Position Vectors is the distance between the two positions.
The normal of a vector is equal to the scalar multiplication of the vector and the reciprocal of the vector's magnitude. This is also called a unit vector, because the length of the normal vector will always be 1 unit (whatever your "unit" is- inches, pixels, miles, etc) The normal represents the direction of a Velocity Vector, just as the magnitude represents the speed of a Velocity Vector. Computing the normal of a Position Vector is not very useful, but computing the normal of the difference between two Position Vectors can be extremely useful.
The Dot Product
The last operation, the dot product, is sometimes the most difficult to grasp. The dot product has a direct relationship to the cosine of the angle between two vectors. In the graphic below, let A and B represent two vectors- Please pretend that there are arrows pointing away from the point denoted by ϴ:

In the picture, A and B share a common point at the symbol ϴ. This makes the explanation easier, but it is not a requirement. For the explanation, A and B represent vectors away from a common point. ϴ represents the angle formed between these two vectors. The dot product of A and B is related to the cosine of the angle ϴ:
$\begin{aligned}A\cdot B=|A||B|\cos\Theta \end{aligned}$
This is a very important relationship, because it leads directly to:
$\begin{aligned}\cos\Theta=\frac{A\cdot B}{|A||B|}\end{aligned}$
... and also ...
$\begin{aligned}\Theta=\cos^{-1}\frac{A\cdot B}{|A||B|}\end{aligned}$
Given two vectors, it is easy to find the angle between them. The last equation is interesting, but unnecessary for our Chaser and Runner. This problem only requires the cosine of the angle.
One interesting note about the dot product is that it allows the computation of the cosine of the angle between two vectors without calling a trigonometric function. Computing a dot product is much faster than computing a cosine. Even if you're writing Assembly Language on a Haswell (circa. ~2013) processor, the FMUL and FSQRT instructions will take 1 clock cycle, while FDIV takes 1 or 2. FCOS alone, however, takes 110 clock cycles. Even if you incorporate latency, the FCOS is still much slower. Reference: Agner Fog's work. Granted, this is a bit orthogonal to the article, but I thought it was interesting.
A brief review of the Law of Cosines
The core component of this algorithm is the Law of Cosines. In the picture above, if A, B and C are treated as the lengths of the sides of the triangle, the Law of Cosines states:
$\begin{aligned}C^2= A^2 + B^2 - 2AB\cos\Theta \end{aligned}$
The graphic is somewhat ambiguous about what A, B and C are. When the graphic is described in the context of the dot product of vectors A, B and C, the context is different than when it is described in terms of trigonometry. If the Law of Cosines is re-stated to use A, B and C in the same way they were used in the dot product description, the Law of Cosines turns into this:
$\begin{aligned}|C|^2= |A|^2 + |B|^2 - 2|A||B|\cos\Theta \end{aligned}$
Remembering the definition of the dot product from above:
$\begin{aligned}A\cdot B=|A||B|\cos\Theta \end{aligned}$
It is evident that the dot product \(|A||B|\cos\Theta\) is equal to the last term of the updated Law of Cosines, giving a new equation:
$\begin{aligned}|C|^2= |A|^2 + |B|^2 - 2(A\cdot B) \end{aligned}$
This yields a Law of Cosines without any trigonometric function calls.
One final review topic- Quadratic equations
A quadratic equation takes the form:
$\begin{aligned}ax^2+bx+c=0\end{aligned}$
where x is the unknown value. To solve the quadratic equation in terms of x, we can use the quadratic formula:
$\begin{aligned}x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\end{aligned}$
If the quadratic equation has a real (non-complex) solution(s), the quadratic formula will provide real value(s) for x.
At this point, I should have enough information to re-describe our Chaser and Runner problem using Vectors and the Law of Cosines.
2D vs 3D
In this simple scenario, the Chaser and the Runner will both be represented by points in a 2D plane. The concepts described here can be converted to a 3D space in a reasonably straight-forward manner because the entirety of the process occurs within a plane. By considering the Chaser, the Runner, and a third point equal to the Runner's position plus some non-zero multiple of its velocity vector, all in 3D space, you have the three unique points necessary for defining any plane in 3D space.
From this, applying a transformation matrix to all coordinates will yield the necessary conversion between 3D and 2D. That's not the topic of this article, however.
The Math Behind the Code
Setting up the problem
I chose "Chaser" and "Runner" because, as I was solving this problem, I kept thinking about "Coyote" and "Roadrunner". Its somewhat common knowledge that the Coyote never really can catch the Roadrunner, but I pretended that he could.
So, imagine the Chaser (Coyote) sees the Runner (Roadrunner). Chaser can tell how fast Runner is as well as the direction Runner is traveling. Chaser also knows how fast he himself can run. By placing himself at the right position, even if Chaser is slower than Runner, there may still be a direction that Chaser can move in order to intercept Runner.
First, lets describe the variables known before using this algorithm. As you can see, I applied my special copyright aversion technique to the picture.

PC = The location of the Chaser, as a Position Vector (x and y coordinates)
PR = The location of the Runner, as a Position Vector
SC = The speed (a scalar) of the Chaser (not shown yet)
VR = The Velocity Vector (speed and direction) of the Runner
From these given inputs, some other basic information can be easily calculated:

SR = The speed (a scalar) of the Runner, equal to the magnitude of VR (not shown)
d = The starting distance between the Chaser and Runner
D = The vector from the Runner to the Chaser
It is apparent in the previous picture that a triangle has emerged. The newly added side is for a vector D, which is equal to PC - PR. Also shown is the length of one side of the triangle labeled "d". This is simply the distance between the Runner and the Chaser. It can be described as the magnitude of vector D, which can be written as either |D| or |PC - PR|.
The pictures have not yet shown either the Runner's or the Chaser's speed. This is because speed needs more context before it can be shown graphically.
But what about the other two lines that look like they form the triangle? What about their lengths?

Note: In this picture, the symbols inside the triangle all denote scalar values (distance or angle), while the symbols outside the triangle denote vectors (Position or Velocity).
There are three new elements in this picture. First is the angle ϴ. ϴ is the angle between vectors D and VR. Remembering our dot product, we know that:
$\begin{aligned}\cos\Theta = \frac{D\cdot V_R}{|D||V_R|}=\frac{D\cdot V_R}{ds_R}\end{aligned}$
It is not completely useful right now, but remember this for later. cos(ϴ) is now defined in terms of values that are already known.
The speed components that were suspiciously absent from the previous pictures have been added to this picture. The length of the vector between PC and PI will be the Chaser's speed sC multiplied by t. t is the amount of time it will take to intersect. t is an unknown- it will be what we "solve for" in a future step. At this point, we simply know that it will take some time t for the interception to occur. This provides the length of the second side of the triangle.
Since we're assuming that there's an interception, and that interception will happen at point PI at some time t in the future, we know that we must take the Runner's speed sR and multiply it by the same time t to give us the distance that the Runner will have to travel before it reaches PI. This provides the length of the last side of the triangle.
Remember, the goal of this algorithm is to calculate the following values:
VC = The Velocity Vector of the Chaser (We know its speed, we need its direction)
PI = The point of interception between the Chaser and Runner
t = The time it will take for interception
.. if its even possible for the two to intercept!
In this section, it is assumed that the Chaser will successfully intercept the Runner. After the math is described, I will explain how to know when the interception cannot happen. This can be for a few different reasons- The Chaser's speed is 0, the Chaser is too slow and already behind, etc. It is easy to detect exactly why a Chaser cannot intercept a Runner.
We have all the setup and information we need to solve the problem!
Applying what is known
The real unknown in the problem is the variable t, the time it will take for the interception to occur. If we know t, then we know everything else in the above picture. PI equals both PC + VCt and PR + VRt . When PR + VRt is known, VC can be found easily enough by setting the two equations equal to each other and solving for VC.
Lets start out by reviewing the inputs to our algorithm. There are no calculations necessary for these values- they are provided:
| Variable | Calculation | Description |
| PC | Given | The current location of the Chaser |
| PR | Given | The current location of the Runner |
| SC | Given | The speed that the Chaser is able to attain |
| VR | Given | The current speed and direction of the Runner |
There are some very basic values calculated directly from these given values:
| Variable | Calculation | Description |
| D | $P_C-P_R$
| A vector from the Runner to the Chaser |
| d | $|D|$
| The distance between the Chaser and the Runner |
| SR | $|V_R|$
| The speed of the runner |
| cos(ϴ) | $\frac{D\cdot V_R}{ds_R}$
| Don't need the actual angle- only the cosine of it |
All of the important stuff is now defined. Next, the Law of Cosines needs to be used on the triangle whose sides are of lengths SCt, SRt and d. Remembering the Law of Cosines:
$\begin{aligned}C^2= A^2 + B^2 - 2AB\cos\Theta \end{aligned}$
Looking at the picture, it should be evident that A, B and C are assigned as follows:
$C=s_Ct$
$B=s_Rt$
$A=d$
... expand those variables into the Law of Cosines equation:
$(s_Ct)^2= (s_Rt)^2+d^2-2ds_Rt\cos \Theta$
... then expand the squares:
$s_C^2t^2= s_R^2t^2+d^2-2ds_Rt\cos \Theta$
... using simple Algebra, the coefficients of t can be moved around to form this equation:
$(s_C^2-s_R^2)t^2+2ds_R\cos\Theta t-d^2=0$
... which is clearly a quadratic equation, as described previously in this article as:
$\begin{aligned}ax^2+bx+c=0\end{aligned}$
... where, in this case, the variables a, b and c take on the following values:
$a=s_C^2-s_R^2$
$b=2ds_R\cos\Theta$
$c=-d^2$
$x=t$
Looking at the "b" component, refer back to the calculation for cos(ϴ) shown above. I'll re-write the "b" component using these two formulae:
$\cos\Theta=\frac{D\cdot V_R}{ds_R}$
$b=2ds_R\cos\Theta$
$b=2ds_R\frac{D\cdot V_R}{ds_R}$
... cancel out the denominator ...
$b=2(D\cdot V_R)$
Its important to note that all of these values are both scalar and they are known at this point. When these values are plugged into the quadratic formula, we get values for t that tell us exactly when the interception will happen.
$\begin{aligned}t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\end{aligned}$
$a=s_C^2-s_R^2$
$b=2(D\cdot V_R)$
$c=-d^2$
Once we know when interception happens, we can apply this time t to the Velocity Vector of the Runner to obtain the point of interception.
$P_I=P_R+V_Rt$
With PI known, we can work with sC and the vector between PI and PC to obtain VC:
$P_I=P_C+V_Ct$
$V_C=\frac{P_I-P_C}{t}$
All three interesting values are now calculated: The Direction that the Chaser needs to run, the Point of Interception between the Chaser and the Runner, and the Time it will take to intercept. The problem is solved, mostly. What about the edge cases, and what happens when interception is not possible?
Interpreting the results of the Quadratic Formula
The Quadratic Formula can return two values for t, as there are two possible correct values for t that satisfy a quadratic equation. Further, it is possible that the equation has no real-valued solutions.
When this part of the quadratic formula
$b^2-4ac$
is negative, the equation has no real-valued solutions. This implies immediately that the Chaser cannot intercept the Runner given the information provided.
Similarly, when both possible values for t are negative, this also means that the only possible chance the Chaser has to intercept the Runner is to go back in time and intercept the Runner in the past. Both t values being negative implies no chance at interception, because we are not pretending that time travel is viable.
When one value of t is negative, and the other positive, then the positive value of t is the one used to determine PI. The negative value is ignored- it represents the notion that the Chaser has to go backward in time to intercept the Runner.
When both values for t are positive, use the smaller of the two values to compute PI. It is assumed that the Chaser wants to intercept sooner rather than later. This is visualized by the following drawing:

Since the Chaser is assumed to have a constant speed, it can intercept the Runner in two places. Note: If the Chaser were allowed to select an arbitrarily slower speed, then the interception could occur anywhere between the two arrows shown in the picture.
Edge Cases where the Law of Cosines and/or the Quadratic Formula doesn't work
Edge Case #1: The Chaser has already caught the Runner (PC ≈ PR)
This is easy- The interception point is PC (or PR), the time is 0, and the velocity vector for the Chaser is (0,0)
Edge Case #2: The Chaser's speed is 0
When the Chaser can't move, obviously interception cannot occur (assuming we checked Edge Case #1 first)
Edge Case #3: The Runner's speed is 0
When the Runner can't move, then the calculations degenerate into these simple equations:
$P_I=P_R$
$t=\frac{d}{s_R}$
$V_C=-s_R\frac{D}{d}$
Edge Case #4: The Runner's Speed equals the Chaser's Speed
If the speed of the Chaser equals that of the Runner, there is no longer a quadratic equation because the "a" value becomes zero. When this happens, a linear equation emerges, and the quadratic formula can not be used (it will try to divide by zero). The quadratic solver I have in this software detects this and replaces the quadratic formula with
$t_1=t_2=-\frac{c}{b}$
when it detects that "a==0". The algorithm implementation depends on this automatic substitution and does not explicitly check for equal speeds.
The math and theory part of this article is now complete. Next comes the software.
The algorithm as a C# method
To jump right into it, here is the C# code for the algortihm itself. Its written such that the reader should be able to tell what's going on without necessarily knowing all of the supporting and helper classes, properties and methods. It was also written to follow the steps performed in the previous section of this article by weaving the "edge cases" and the "assume interception" case together in a manner that makes sense:
private void SetResults()
{
if (m_calculationPerformed)
return;
ClearResults();
m_calculationPerformed = true;
if (!HasValidInputs)
return;
if (ChaserPosition.AreSame( RunnerPosition ))
{
m_interceptionPossible = true;
m_interceptionPosition = ChaserPosition;
m_timeToInterception = 0;
m_chaserVelocity = SVector2d.Zero;
return;
}
if (ChaserSpeed <= 0)
return;
SVector2d vectorFromRunner = ChaserPosition - RunnerPosition;
double distanceToRunner = vectorFromRunner.Length;
double runnerSpeed = RunnerVelocity.Length;
if (runnerSpeed.IsClose( 0 ))
{
m_timeToInterception = distanceToRunner / ChaserSpeed;
m_interceptionPosition = RunnerPosition;
}
else
{
double a = ChaserSpeed * ChaserSpeed - runnerSpeed * runnerSpeed;
double b = 2 * vectorFromRunner.Dot( RunnerVelocity );
double c = -distanceToRunner * distanceToRunner;
double t1, t2;
if (!CMath.QuadraticSolver( a, b, c, out t1, out t2 ))
{
return;
}
if (t1 < 0 && t2 < 0)
{
return;
}
if (t1 > 0 && t2 > 0)
m_timeToInterception = Math.Min( t1, t2 );
else
m_timeToInterception = Math.Max( t1, t2 );
m_interceptionPosition = RunnerPosition + RunnerVelocity * m_timeToInterception;
}
m_chaserVelocity = (m_interceptionPosition - ChaserPosition) / m_timeToInterception;
m_interceptionPossible = true;
}
The method attempts to prove that interception cannot occur at various points. When this is proven, the routine returns immediately. I apologize to those purist readers who insist that there should be exactly one exit point for every method- I don't always agree with you, but I respect your opinion.
Things to note about the class that has this method in it:
- The class has four read/write properties, one for each of the input values
ChaserPosition, ChaserSpeed, RunnerPosition, and RunnerVelocity - The class has three read-only properties for the main outputs:
ChaserVelocity, TimeToInterception, and InterceptionPoint. Accessing any of these values trigger a re-compute of the data iff any of the input data has changed - The class has a read-only property
InterceptionPossible that denotes whether or not interception is even possible for the given inputs. - The class has a read-only property
HasValidInputs that is TRUE when all of the input values have been set to valid values. By default, they have invalid values and the application is required to set them all. - All properties are immutable ValueTypes. If they weren't, this usage pattern would not work.
Things to note about the vector class:
- It is an immutable ValueType
- It has an arithmetic usage pattern (e.g. P + Q) as well as a Fluent usage pattern (e.g. P.AddTo( Q ) )
- It supports "invalid values" by setting either X or Y to NaN (or to either Infinity).
There is another helper class called CMath which, among other things, contains:
- Testing for "close" double-precision values. If you don't like my version of what "close" is, please feel free to change the value to something that suits you.
- A Quadratic Equation solver
Using the class
In the following example, the use of the class containing the Interception algorithm looks like this:
var intercept = new CInterceptCalculator2d()
{
ChaserPosition = coyote.Position,
ChaserSpeed = coyote.Speed,
RunnerPosition = roadrunner.Position,
RunnerVelocity = roadrunner.Velocity
};
if (!intercept.InterceptionPossible)
Console.Writeline( "The coyote is too slow to intercept the roadrunner" );
coyote.Velocity = intercept.ChaserVelocity;
The class CInterceptCalculator2d maintains an internal state that detects every time one of its input properties is changes. When one of the output properties is queried, it will check to see if any input has changed since the last calculation, and re-calculate if necessary. The application is not required to call any special method to perform the calculation- Just query an output value once all of the input values have been set and the correct answer will be provided.
If the inputs have not all been set, the output values will equal SVector2d.NotAVector. The following could be used to detect this case:
var intercept = new CInterceptCalculator2d()
{
ChaserPosition = coyote.Position,
ChaserSpeed = coyote.Speed,
RunnerVelocity = roadrunner.Velocity
};
assert( ! intercept.ChaserVelocity.IsAVector )
assert( intercept.InterceptionPoint == SVector2d.NotAVector )
The Simulator- Contents of the ZIP file
Attached to this article is a simulator which visualizes the use of the interception algorithm. This is a Windows Forms application. When run, the user will see a "pigeon" (a white dot) running across the top of the screen. He will also see a "gun" (a red dot) with a gun-barrel (a red line). The barrel will always be pointed at where the bullet (a green dot) needs to be fired in order to hit the moving pigeon.
The user will be able to drag the gun around the screen to see how this affects the angle of the gun barrel. When the user presses the 'F' key, the bullet will be fired from the gun, traveling in a straight line until it hits the pigeon. If the pigeon changes direction while the bullet is in flight, the bullet will obviously miss the pigeon.
CInterceptCalculator.cs
This is the main intercept calculator object.
SVector2d.cs
This file contains the entirety of my vector class. There is stuff in here not immediately used by this application, but hopefully you will find something interesting in here.
CMath.cs
A collection of helper and convenience methods I have written over the years. Mainly provides the quadratic formula and the "IsClose" functionality to this application.
CMovableObject.cs, CCircle.cs, CRectangle.cs
These are the movable objects used by the simulation. The rectangle isn't used in this simulation.
FInterceptSimulation.cs
This is the main Windows Form that contains the simulation. There is no MVC pattern here- Its a simple test program to show the functionality of the interception algorithm.
If any of the code in these files is unclear to you, please feel free to ask and I'll be happy to answer your questions.
Points of Interest
I wrote the substance of this article for a class I was asked to develop on video game artificial intelligence. This was one of the topics for the class. I had never really thought about what goes into interception before- I had always thought it was an easy problem to solve (of course "easy" being the ambiguous word here...)
While none of the individual concepts presented in this article are "hard" in any way, putting it all together was a fun exercise. Since then, I have used this topic as a guest instructor for another video game development class, and have now polished it up for consumption by the CodeProject audience.
