
Introduction
The Fast Fourier Transform (FFT) allows users to view the spectrum content of an audio signal. The FFT code presented here was written by Don Cross, his homepage appears to have subsequently been taken down. Rather than explain the mathematical theory of the FFT, I will attempt to explain its usefulness as it relates to audio signals.
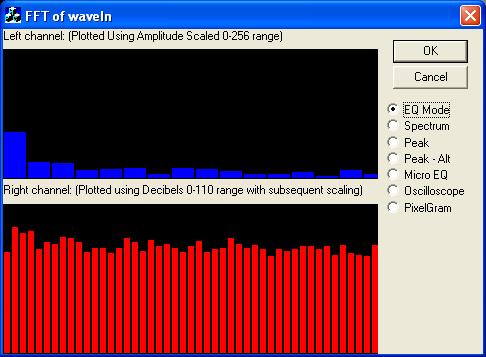
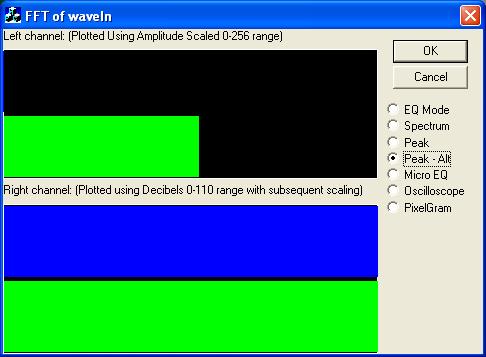
The FFT allows users to obtain the spectral makeup of an audio signal, obtain the decibels of its various frequencies, or obtain the intensity of its various frequencies. Spectral viewers (shown in the image above), Equalizers, or VU-Meters may all use the FFT in order to display their results. The difference between them then depends upon one of a couple of equations that take the real and imaginary components of the FFT, and return either the intensity or decibel levels to be used in the graphed result. The following code takes both the real and imaginary components of the FFT result, and returns the intensity and decibels.
inline double GetFrequencyIntensity(double re, double im)
{
return sqrt((re*re)+(im*im));
}
#define mag_sqrd(re,im) (re*re+im*im)
#define Decibels(re,im) ((re == 0 && im == 0) ? (0) :
10.0 * log10(double(mag_sqrd(re,im))))
#define Amplitude(re,im,len) (GetFrequencyIntensity(re,im)/(len))
#define AmplitudeScaled(re,im,len,scale) ((int)Amplitude(re,im,len)%scale)
The FFT uses the audio signal as its real component, and uses a NULL pointer for its imaginary component indicating that the imaginary data does not exist. Upon its return, the FFT will return both the real and imaginary data components based upon the data given as the real component. The is mirrored with the return samples so that 0-FFT_LEN/2 contains the data, and FFT_LEN/2 to FFT_LEN contains a reverse of the data. This mistake was corrected in my code. The code that performs the FFT follows:
DWORD nCount = 0;
for (DWORD dw = 0; dw < FFT_LEN; dw++)
{
{
finleft[nCount] = (double)((short*)pwh->lpData)[dw++];
finright[nCount++] = (double)((short*)pwh->lpData)[dw];
}
}
fft_double(FFT_LEN/2,0,finleft,NULL,fout,foutimg);
float re,im,fmax=-99999.9f,fmin=99999.9f;
for(int i=1;i < FFT_LEN/4-1;i++)
{
re = fout[i];
im = foutimg[i];
fdraw[i]=AmplitudeScaled(re,im,FFT_LEN/2,256);
if (fdraw[i] > fmax)
{
fmax = fdraw[i];
}
if (fdraw[i] < fmin)
{
fmin = fdraw[i];
}
}
int nAvg, nBars=16, nCur = 0;
for(int i=1;i < FFT_LEN/4;i++)
{
nAvg = 0;
for (int n=0; n < nBars; n++)
{
nAvg += (int)fdraw[i];
}
nAvg /= nBars;
TRACE("Average for Bar#%d is %d\n",nCur++,nAvg);
i+=nBars-1;
}
DataHolder* pDataHolder = (DataHolder*)lpData;
CFrequencyGraph* pPeak = (CFrequencyGraph*)pDataHolder->pData;
if (::IsWindow(pPeak->GetSafeHwnd()))
{
pPeak->SetYRange(0,256);
pPeak->Update(FFT_LEN/4,fdraw);
}
fmax=-99999.9f,fmin=99999.9f;
fft_double(FFT_LEN/2,0,finright,NULL,fout,foutimg);
fdraw[0] = fdraw[FFT_LEN/4] = 0;
for(i=1;i < FFT_LEN/4-1;i++)
{
re = fout[i];
im = foutimg[i];
fdraw[i] = Decibels(re,im);
if (fdraw[i] > fmax)
{
fmax = fdraw[i];
}
if (fdraw[i] < fmin)
{
fmin = fdraw[i];
}
}
CFrequencyGraph* pPeak2 = (CFrequencyGraph*)pDataHolder->pData2;
if (::IsWindow(pPeak2->GetSafeHwnd()))
{
pPeak2->SetNumberOfSteps(50);
pPeak2->SetYRange((int)fmin,(int)fmax);
pPeak2->Update(FFT_LEN/4,fdraw);
}
This code is contained in a callback function that is called every time the waveIn functions return with updated audio signal data. The code that actually performs the FFT looks like:
void fft_double (unsigned int p_nSamples, bool p_bInverseTransform,
double *p_lpRealIn, double *p_lpImagIn,
double *p_lpRealOut, double *p_lpImagOut)
{
if(!p_lpRealIn || !p_lpRealOut || !p_lpImagOut) return;
unsigned int NumBits;
unsigned int i, j, k, n;
unsigned int BlockSize, BlockEnd;
double angle_numerator = 2.0 * PI;
double tr, ti;
if( !IsPowerOfTwo(p_nSamples) )
{
return;
}
if( p_bInverseTransform ) angle_numerator = -angle_numerator;
NumBits = NumberOfBitsNeeded ( p_nSamples );
for( i=0; i < p_nSamples; i++ )
{
j = ReverseBits ( i, NumBits );
p_lpRealOut[j] = p_lpRealIn[i];
p_lpImagOut[j] = (p_lpImagIn == NULL) ? 0.0 : p_lpImagIn[i];
}
BlockEnd = 1;
for( BlockSize = 2; BlockSize <= p_nSamples; BlockSize <<= 1 )
{
double delta_angle = angle_numerator / (double)BlockSize;
double sm2 = sin ( -2 * delta_angle );
double sm1 = sin ( -delta_angle );
double cm2 = cos ( -2 * delta_angle );
double cm1 = cos ( -delta_angle );
double w = 2 * cm1;
double ar[3], ai[3];
for( i=0; i < p_nSamples; i += BlockSize )
{
ar[2] = cm2;
ar[1] = cm1;
ai[2] = sm2;
ai[1] = sm1;
for ( j=i, n=0; n < BlockEnd; j++, n++ )
{
ar[0] = w*ar[1] - ar[2];
ar[2] = ar[1];
ar[1] = ar[0];
ai[0] = w*ai[1] - ai[2];
ai[2] = ai[1];
ai[1] = ai[0];
k = j + BlockEnd;
tr = ar[0]*p_lpRealOut[k] - ai[0]*p_lpImagOut[k];
ti = ar[0]*p_lpImagOut[k] + ai[0]*p_lpRealOut[k];
p_lpRealOut[k] = p_lpRealOut[j] - tr;
p_lpImagOut[k] = p_lpImagOut[j] - ti;
p_lpRealOut[j] += tr;
p_lpImagOut[j] += ti;
}
}
BlockEnd = BlockSize;
}
if( p_bInverseTransform )
{
double denom = (double)p_nSamples;
for ( i=0; i < p_nSamples; i++ )
{
p_lpRealOut[i] /= denom;
p_lpImagOut[i] /= denom;
}
}
}
And it requires the following supporting functions:
bool IsPowerOfTwo( unsigned int p_nX )
{
if( p_nX < 2 ) return false;
if( p_nX & (p_nX-1) ) return false;
return true;
}
unsigned int NumberOfBitsNeeded( unsigned int p_nSamples )
{
int i;
if( p_nSamples < 2 )
{
return 0;
}
for ( i=0; ; i++ )
{
if( p_nSamples & (1 << i) ) return i;
}
}
unsigned int ReverseBits(unsigned int p_nIndex, unsigned int p_nBits)
{
unsigned int i, rev;
for(i=rev=0; i < p_nBits; i++)
{
rev = (rev << 1) | (p_nIndex & 1);
p_nIndex >>= 1;
}
return rev;
}
double Index_to_frequency(unsigned int p_nBaseFreq,
unsigned int p_nSamples, unsigned int p_nIndex)
{
if(p_nIndex >= p_nSamples)
{
return 0.0;
}
else if(p_nIndex <= p_nSamples/2)
{
return ( (double)p_nIndex /
(double)p_nSamples * p_nBaseFreq );
}
else
{
return ( -(double)(p_nSamples-p_nIndex) /
(double)p_nSamples * p_nBaseFreq );
}
}
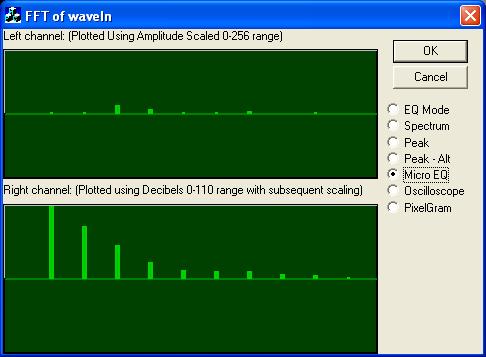
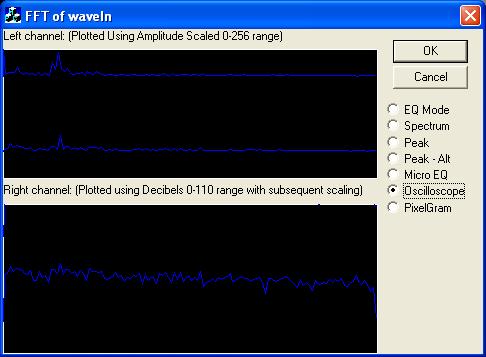
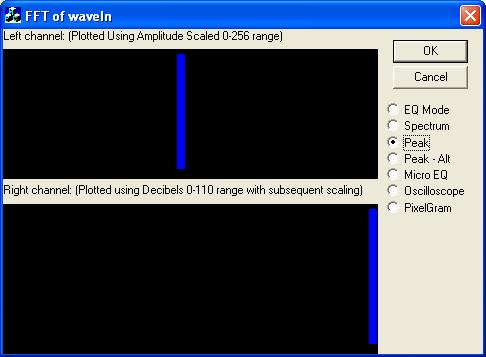
The included sample class, CFrequencyGraph, will draw a sample EQ, peak meter, and spectral graph using the frequency intensity. Hopefully, this serves as a decent introduction to the uses and basics of the Fast Fourier Transform for audio signals. Other functions of the FFT include using it in combination with a Beat Detection Algorithm to detect beats in an audio signal. Another page with useful FFT information is located at FFT Spectrum Analyser.
This article uses waveIn* functions to retrieve the soundcard's data from the playing source. Therefore, you must manually open your soundcard properties and change the recording source to use mono/stereo mix or waveIn as the selected recording line. Also, if you set the playback wave option to false, this will override the recording options and no sound will appear. For information about doing an inverse FFT for transforming frequencies into an audio signal, please do a Google search on "Inverse FFT" or "IFFT".
History
- Version 1.3: Fixed Spectrum drawing, Changed Pixelgram color, changed Process routine to match new Recording parameters.
- Version 1.2: Fixed many drawing bugs, changed to use amplitude scaled and decibels.
