More Texas Holdem Analysis in C#: Part 2

Keith Rule

4.93/5 (32 votes)

20 May 2008LGPL327 min read

2.9K

Using C# to do sophisticated analysis of Texas Holdem

Download source - 1.34 MB

Introduction

In Part 1 of this article, you will find the following topics covered:

Pocket Query Language - This offers a straightforward set of methods that allow you experiment with different pocket hand combinations without rewriting your code.
Outs and draw methods - Determining outs and draws is key to analyzing a situation. This section discusses techniques for doing just that.

In this article, we will cover the following topics.

Monte Carlo analysis - Sometimes quick estimates are good enough. Monte Carlo analysis makes it possible to make high quality estimates in a very short time.
Multi-player hand analysis - More often than not, you are playing against multiple players. Here's how to calculate win odds against multiple players in a reasonable amount of time.
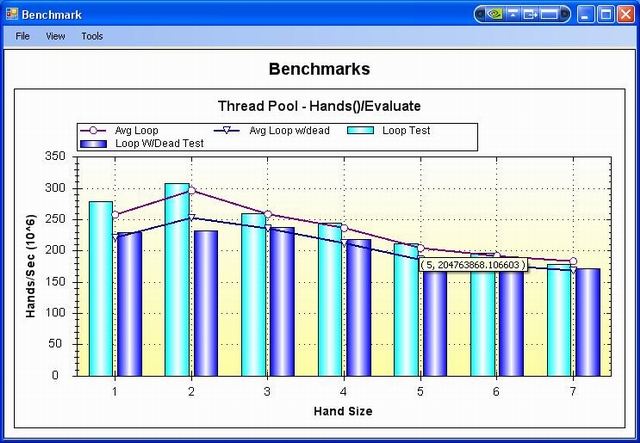
Multiple core support - The speed-ups are nearly linear when adding cores. Notice that the benchmark image above shows over 204 million hands/second calculated on a dual Quad Core system.

Monte Carlo analysis

Monte Carlo analysis can be used in analyzing poker hands. There are many reasons people choose to use Monte Carlo Analysis. In poker, the most common reason is to get a quick answer for something that otherwise would take a prohibitively long time to calculate. I resisted using Monte Carlo analysis for quite some time. I clung to my wish that a sufficiently fast Poker Hand Evaluator Library would eliminate the need for woo-woo techniques like this. To convince myself of the value of Monte Carlo analysis, I had to work through the analysis of win odds for one or more players. The following two sections go through my logic for accepting Monte Carlo analysis. Hopefully you will see the value of it and how easy it is to do.

Calculating win odds

Consider the following code. It calculates the win odds for a player being dealt AKs against a random opponent.

This program takes about 299 seconds (nearly 5 minutes) on my laptop to calculate with no board cards. That means the code is evaluating 14,084,025 hands/sec and a total of 2,097,572,400 (yes, billions) of hand match-ups. With three cards on the board, it takes 0.263 seconds and a total of 1,070,190 hand match-ups.

When there are cards on the board, this function is very usable. However, if you are calculating hole card win probabilities with this, then the algorithm is far too slow to be usable.

using System;
using System.Collections.Generic;
using HoldemHand;

namespace ConsoleApplication1
{
    class Program
    {
        static void Main(string[] args)
        {
            // This code calculates the probablity of As Ks winning against
            // another random hand.            
            ulong pocketmask = Hand.ParseHand("As Ks");  // Hole hand  
            ulong board = Hand.ParseHand("");            // No board cards yet
            long wins = 0, ties = 0, loses = 0, count = 0;  
                // Iterate through all possible opponent hole cards 
            foreach (ulong oppmask in Hand.Hands(0UL, board | pocketmask, 2))
            {
                // Iterate through all board cards      
                foreach (ulong boardmask in Hand.Hands(
                    board, pocketmask | oppmask, 5))
                {
                    // Evaluate the player and opponent hands and 
                    // tally the results    
                    uint pocketHandVal = 
                        Hand.Evaluate(pocketmask | boardmask, 7);
                    uint oppHandVal = Hand.Evaluate(oppmask | boardmask, 7);
                    if (pocketHandVal > oppHandVal)
                    {
                        wins++;
                    }
                    else if (pocketHandVal == oppHandVal)
                    {
                        ties++;
                    }
                    else
                    {
                        loses++;
                    }
                    count++;
                }
            }
            // Prints: Win 67.0446323092352%   
            Console.WriteLine("Win {0}%",
                (((double)wins) + ((double)ties) / 2.0) / (
                    (double)count) * 100.0);
        }
    }
}

I've gotten around problems like this in the past by pre-calculating the exact values and then using lookup tables. However, there many situations in Texas Holdem where the computation time required is very long and lookup tables aren't feasible, such as calculating odds win odds against multiple players. Because of this, other techniques need to be considered for some problems. That's why I first looked into Monte Carlo analysis.

Getting "good enough" results fast

I'm not a perfectionist and apparently neither are many of the successful professional Texas Holdem Players.

In Phil Gordon's Little Green Book -- a very good book, I might add -- he describes a very simple heuristic that can be calculated in your head and that gives the approximate odds of hitting your "outs." He calls this "the rule of 4 and 2." The way this heuristic works is that you count your outs. If you've just seen the flop and not the turn card, then multiply the outs by 4 and you will have the approximate percentage of hitting your outs. If you've seen the turn but not the river, you multiply the outs by 2 to get the approximate odds of hitting your outs.

These types of simple estimates are used by many of the professional players to help evaluate their situation. If an estimate is good enough for them, then it's probably good enough for the rest of us if used correctly. Monte Carlo Analysis is just a method for a computer to quickly estimate the odds in a specific situation.

Consider our previous example of calculating the win odds for AKs. It would take 299 seconds to iterate through all the possible situations and give us an exact answer. The following table was calculated using Monte Carlo analysis. The number on the left is the number of trials and the second number is the estimated win odds. The exact odds were 67.0446323092352%. The third column is the difference between the exact answer and the estimate answer. The fourth column is the time taken in seconds.

Trials	Wins	Difference	Duration
10	80.00%	12.9554	0.00005
50	68.00%	0.9554	0.00007
100	61.00%	6.0446	0.00009
500	68.90%	1.8554	0.00038
1000	67.10%	0.0554	0.00071
5000	68.32%	1.2754	0.00345
10000	67.15%	0.1004	0.00759
15000	66.52%	0.5246	0.01065
20000	67.96%	0.9104	0.01451
25000	66.84%	0.2006	0.01772
30000	67.00%	0.0480	0.02197
40000	67.05%	0.0029	0.02837
50000	67.16%	0.1184	0.03610
100000	67.19%	0.1449	0.07154
150000	66.98%	0.0663	0.10710
200000	66.96%	0.0856	0.15701
500000	66.94%	0.1018	0.36579
1000000	67.04%	0.0024	0.79401
2000000	67.04%	0.0025	1.43816
5000000	67.05%	0.0023	3.84238
10000000	67.03%	0.0110	7.76830
20000000	67.04%	0.0092	15.02408

Notice that at 0.00071 seconds (0.7 milliseconds) we have 2 good digits. At 0.02197 (22 milliseconds) we have about 3 good digits. At 0.79401 (794 milliseconds) we have 4 good digits. It's easy to see that we can get very good estimates in well less than a second. The following code was used to generate the previous table.

using System;
using System.Collections.Generic;
using System.Runtime.InteropServices;
using HoldemHand;

namespace WinOddsMonteCarlo
{    
    /// 
    /// This program shows the increase in accuracy of the Monte Carlo method
    /// when increasing the number of samples.
    /// 
    class Program    
    {        
        static void Main(string[] args)        
        {            
            // This code calculates the probablity of As Ks winning against
            // another random hand.            
            ulong pocketmask = Hand.ParseHand("As Ks"); // Hole hand      
            ulong board = Hand.ParseHand("");           // No board cards yet
            // Trial numbers 
            int[] trialsTable = {                
                10, 50, 100, 500, 1000, 5000, 10000, 15000, 20000, 
                25000, 30000, 40000, 50000, 100000, 150000, 200000,  
                500000, 1000000, 2000000, 5000000, 10000000, 20000000  
            };       
            // timer values  
            double start = 0.0;    
     
            Console.WriteLine("Trials,Wins,Difference,Duration");  
   
            foreach (int trials in trialsTable) 
            {    
                long wins = 0, ties = 0, count = 0;
                // Get start time  
                start = Hand.CurrentTime;   
                // Iterate through a series board cards  
                foreach (ulong boardmask in Hand.RandomHands(board, 
                    pocketmask, 5, trials)) 
                {
                    // Get a random opponent hand 
                    ulong oppmask = 
                        Hand.RandomHand(boardmask | pocketmask, 2);  
                    // Evaluate the player and opponent hands
                    uint pocketHandVal = 
                        Hand.Evaluate(pocketmask | boardmask, 7); 
                    uint oppHandVal = Hand.Evaluate(oppmask | boardmask, 7;
                    // Calculate Statistics 
                    if (pocketHandVal > oppHandVal) 
                    {
                        wins++;   
                    }  
                    else if (pocketHandVal == oppHandVal)
                    {  
                        ties++; 
                    }
                    count++;   
                }

                double duration = Hand.CurrentTime - start;
                // Correct answer is 67.0446323092352%   
                Console.WriteLine("{0},{1:0.00}%,{2:0.0000},{3:0.00000}",
                    trials, 
                    (((double)wins) + (
                    (double)ties) / 2.0) / ((double)count) *100.0, 
                    Math.Abs(67.0446323092352 - ((((double)wins) +
                    ((double)ties) / 2.0) / ((double)count) * 100)), 
                    duration);            
            }        
        }    
    }
}

Monte Carlo analysis helper methods

The following method is intentionally similar to the IEnumerable Hands(ulong shared, ulong dead, int ncards) method. One additional argument is added, which is the number of random hands that are to be iterated through by this enumerator.

public static IEnumerable RandomHands(
    ulong shared, ulong dead, int ncards, int trials)

This IEnumerable method allows the foreach command to iterate through random hands. The hands returned must meet the criterion specified. The number of hands specified in the last argument are returned.

public static IEnumerable RandomHands(
    ulong shared, ulong dead, int ncards, double duration)

This method is similar to the previous method. However, rather than specifying the number of trials, a time duration is specified. This allows a time budget to be specified for getting an answer. I have a mild preference to using this version of these methods.

Calculating win odds for multiple players

It's interesting to calculate odds against one player. However, more often than not, you are playing against multiple players. The following example shows how to calculate the win odds for the same situation with 1 through 9 players.

using System;
using HoldemHand;

// This example calculates the win odds for a player having "As Ks" against 
// 1-9 random players
namespace WinOddsMultipleOpponents
{
    class Program
    {
        // Expected output (approximate values)
        // 1: win 67.08%
        // 2: win 50.82%
        // 3: win 41.53%
        // 4: win 35.46%
        // 5: win 31.13%
        // 6: win 27.82%
        // 7: win 24.99%
        // 8: win 22.77%
        // 9: win 20.77%
        static void Main(string[] args)
        {
            const double time = 5.0;
            ulong pocket = Hand.ParseHand("As Ks");
            ulong board = Hand.ParseHand("");
            ulong dead = Hand.ParseHand("");

            for (int opponents = 1; opponents <= 9; opponents++)
            {
                Console.WriteLine("{0}: win {1:0.00}%", 
                    opponents, WinOddsMonteCarlo(
                    pocket, board, dead, opponents, time) * 100.0);
            }
        }

        // An example of how to calculate win odds for multiple players
        static double WinOddsMonteCarlo(
            ulong pocket, ulong board, ulong dead, int nopponents, 
            double duration)
        {
            System.Diagnostics.Debug.Assert(
                nopponents > 0 && nopponents <= 9);
            System.Diagnostics.Debug.Assert(
                duration > 0.0);
            System.Diagnostics.Debug.Assert(
                Hand.BitCount(pocket) == 2);
            System.Diagnostics.Debug.Assert(
                Hand.BitCount(board) >= 0 && Hand.BitCount(board) <= 5);

            // Keep track of stats
            double win = 0.0, count = 0.0;

            // Keep track of time
            double start = Hand.CurrentTime;

            // Loop for specified time duration
            while ((Hand.CurrentTime-start) < duration)
            {
                // Player and board info
                ulong boardmask = Hand.RandomHand(board, dead | pocket, 5);
                uint playerHandVal = Hand.Evaluate(pocket | boardmask);

                // Ensure that dead, board, and pocket cards are not
                // available to opponent hands.
                ulong deadmask = dead | boardmask | pocket;

                // Comparison Results
                bool greaterthan = true;
                bool greaterthanequal = true;

                // Get random opponent hand values
                for (int i = 0; i < nopponents; i++)
                {
                    // Get Opponent hand info
                    ulong oppmask = Hand.RandomHand(deadmask, 2);
                    uint oppHandVal = Hand.Evaluate(oppmask | boardmask);

                    // Remove these opponent cards from future opponents
                    deadmask |= oppmask;

                    // Determine compare status
                    if (playerHandVal < oppHandVal)
                    {
                        greaterthan = greaterthanequal = false;
                        break;
                    }
                    else if (playerHandVal <= oppHandVal)
                    {
                        greaterthan = false;
                    }
                }

                // Calculate stats
                if (greaterthan)
                    win += 1.0;
                else if (greaterthanequal)
                    win += 0.5;

                count += 1.0;
            }

            // Return stats
            return (count == 0.0 ? 0.0 : win/count);
        }
    }
}

The method WinOddsMonteCarlo does all of the hard work here. You will notice that the results for a single opponent appear to be accurate to 3 digits when compared against our previous calculation. I can't vouch for the digits of accuracy for opponent counts greater than 1 -- frankly, it takes too long to get answers -- but the values are very stable when plotted on the MultiOddsApp application. You'll find MultiOddsApp in the demo programs included in the downloadable project. Because of this, I believe that the results are reasonably accurate.

Calculating win odds for all pocket hands

A simple variation of the above program can be used to calculate the approximate win odds for each of the 169 possible starting pocket hands for 1-9 opponents. Note that I've include the resulting table that gives approximate odds for a representative example of every possible starting hand for 1 though 9 opponents. I haven't run across the equivalent information online and thought that might be interesting for some players.

using System;
using HoldemHand;

// This example calculates the win odds for a player having "As Ks" against 
// 1-9 random players. The results is comma separated so that 
// it can be imported
// into Excel using the .csv file type.
namespace WinOddsMultipleOpponentsTable
{
    class Program
    {
        static void Main(string[] args)
        {
            const double time = 5.0;
            ulong board = Hand.ParseHand("");
            ulong dead = Hand.ParseHand("");

            // Table Header
            Console.Write(",");
            for (int i = 1; i <= 9; i++)
            {
                Console.Write("{0},", i);
            }
            Console.WriteLine();

            // Iterates through one representative hand of each of the 
            // 169 possible
            // pocket hand types
            foreach (ulong pocket in PocketHands.Hands169())
            {
                // Show Pocker Hand
                Console.Write("\"{0}\",", Hand.MaskToString(pocket));

                // Calculate and Display the Approximate odds for 1-9 
                // opponents
                for (int opponents = 1; opponents <= 9; opponents++)
                {
                    Console.Write("{0}%,", WinOddsMonteCarlo(
                        pocket, board, dead, opponents, time) * 100.0);
                }
                Console.WriteLine();
            } 
        }

        // An example of how to calculate win odds for multiple players
        static double WinOddsMonteCarlo(ulong pocket, ulong board, ulong dead, 
            int nopponents, double duration)
        {
            System.Diagnostics.Debug.Assert(
                nopponents > 0 && nopponents <= 9);
            System.Diagnostics.Debug.Assert(duration > 0.0);
            System.Diagnostics.Debug.Assert(Hand.BitCount(pocket) == 2);
            System.Diagnostics.Debug.Assert(
                Hand.BitCount(board) >= 0 && Hand.BitCount(board) <= 5);

            // Keep track of stats
            double win = 0.0, count = 0.0;

            // Keep track of time
            double start = Hand.CurrentTime;

            // Loop for specified time duration
            while ((Hand.CurrentTime-start) < duration)
            {
                // Player and board info
                ulong boardmask = Hand.RandomHand(board, dead | pocket, 5);
                uint playerHandVal = Hand.Evaluate(pocket | boardmask);

                // Ensure that dead, board, and pocket cards are not
                // available to opponent hands.
                ulong deadmask = dead | boardmask | pocket;

                // Comparison Results
                bool greaterthan = true;
                bool greaterthanequal = true;

                // Get random opponent hand values
                for (int i = 0; i < nopponents; i++)
                {
                    // Get Opponent hand info
                    ulong oppmask = Hand.RandomHand(deadmask, 2);
                    uint oppHandVal = Hand.Evaluate(oppmask | boardmask);

                    // Remove these opponent cards from future opponents
                    deadmask |= oppmask;

                    // Determine compare status
                    if (playerHandVal < oppHandVal)
                    {
                        greaterthan = greaterthanequal = false;
                        break;
                    }
                    else if (playerHandVal <= oppHandVal)
                    {
                        greaterthan = false;
                    }
                }

                // Calculate stats
                if (greaterthan)
                    win += 1.0;
                else if (greaterthanequal)
                    win += 0.5;

                count += 1.0;
            }

            // Return stats
            return (count == 0.0 ? 0.0 : win/count);
        }
    }
}

The resulting output is below. This table gives the approximate odds of winning, given the specified pocket hand against the number of specified opponents. Each cell was given 30 seconds of calculation time, so the results are probably good to several digits. However, I haven't verified that for opponent numbers greater then 1.

Pocket Cards vs Approximate Win Odds Given Opponent Count
	1	2	3	4	5	6	7	8	9
As Ah	85.20%	73.50%	63.91%	55.91%	49.24%	43.59%	38.75%	34.66%	31.14%
Ks Kh	82.40%	68.93%	58.30%	49.88%	43.01%	37.46%	32.95%	29.24%	26.15%
Qs Qh	79.93%	64.98%	53.58%	44.79%	37.92%	32.58%	28.35%	24.98%	22.28%
Js Jh	77.46%	61.22%	49.25%	40.32%	33.63%	28.59%	24.70%	21.71%	19.40%
Ts Th	75.01%	57.63%	45.27%	36.41%	30.00%	25.27%	21.82%	19.17%	17.20%
9s 9h	72.06%	53.70%	41.21%	32.65%	26.70%	22.50%	19.47%	17.26%	15.61%
8s 8h	69.16%	50.01%	37.67%	29.56%	24.09%	20.38%	17.77%	15.91%	14.55%
7s 7h	66.23%	46.56%	34.48%	26.85%	21.96%	18.69%	16.44%	14.87%	13.70%
6s 6h	63.29%	43.29%	31.60%	24.59%	20.19%	17.36%	15.44%	14.09%	13.10%
5s 5h	60.32%	40.17%	29.01%	22.54%	18.63%	16.16%	14.50%	13.33%	12.43%
4s 4h	57.02%	36.88%	26.41%	20.69%	17.37%	15.34%	13.93%	12.98%	12.21%
3s 3h	53.69%	33.77%	24.12%	19.14%	16.35%	14.67%	13.56%	12.75%	12.08%
2s 2h	50.33%	30.82%	22.10%	17.86%	15.62%	14.24%	13.30%	12.59%	11.99%
As Ks	67.03%	50.82%	41.53%	35.50%	31.16%	27.80%	25.06%	22.73%	20.79%
As Kh	65.31%	48.29%	38.64%	32.41%	27.94%	24.48%	21.68%	19.33%	17.30%
As Qs	66.21%	49.50%	39.97%	33.81%	29.42%	26.09%	23.39%	21.19%	19.37%
As Qh	64.44%	46.89%	36.94%	30.56%	26.04%	22.59%	19.82%	17.56%	15.66%
As Js	65.37%	48.27%	38.56%	32.36%	27.98%	24.72%	22.12%	20.03%	18.30%
As Jh	63.56%	45.57%	35.40%	28.99%	24.46%	21.04%	18.39%	16.21%	14.43%
As Ts	64.59%	47.15%	37.35%	31.12%	26.84%	23.65%	21.16%	19.15%	17.48%
As Th	62.74%	44.38%	34.08%	27.62%	23.16%	19.85%	17.26%	15.20%	13.50%
As 9s	62.77%	44.64%	34.63%	28.45%	24.27%	21.18%	18.85%	17.02%	15.52%
As 9h	60.76%	41.65%	31.19%	24.70%	20.36%	17.19%	14.77%	12.86%	11.34%
As 8s	61.93%	43.62%	33.58%	27.48%	23.35%	20.39%	18.12%	16.35%	14.92%
As 8h	59.87%	40.53%	30.03%	23.64%	19.36%	16.30%	13.95%	12.13%	10.65%
As 7s	60.98%	42.47%	32.50%	26.52%	22.51%	19.68%	17.49%	15.81%	14.43%
As 7h	58.83%	39.32%	28.86%	22.60%	18.44%	15.47%	13.24%	11.51%	10.13%
As 6s	59.90%	41.25%	31.41%	25.58%	21.74%	19.01%	16.96%	15.35%	14.06%
As 6h	57.67%	37.99%	27.67%	21.56%	17.57%	14.75%	12.65%	11.02%	9.74%
As 5s	59.94%	41.52%	31.87%	26.13%	22.31%	19.61%	17.56%	15.96%	14.61%
As 5h	57.71%	38.26%	28.13%	22.14%	18.20%	15.37%	13.27%	11.62%	10.31%
As 4s	59.01%	40.63%	31.10%	25.50%	21.81%	19.19%	17.21%	15.64%	14.35%
As 4h	56.72%	37.29%	27.29%	21.43%	17.61%	14.91%	12.87%	11.30%	10.04%
As 3s	58.22%	39.73%	30.33%	24.89%	21.30%	18.77%	16.84%	15.34%	14.09%
As 3h	55.86%	36.33%	26.47%	20.75%	17.06%	14.46%	12.51%	10.97%	9.74%
As 2s	57.37%	38.86%	29.58%	24.20%	20.75%	18.27%	16.40%	14.91%	13.73%
As 2h	54.93%	35.37%	25.57%	19.99%	16.42%	13.90%	12.02%	10.52%	9.33%
Ks Qs	63.40%	47.19%	38.30%	32.58%	28.45%	25.24%	22.66%	20.51%	18.74%
Ks Qh	61.47%	44.48%	35.28%	29.39%	25.15%	21.84%	19.21%	17.02%	15.21%
Ks Js	62.58%	45.98%	36.94%	31.18%	27.08%	23.95%	21.45%	19.44%	17.76%
Ks Jh	60.58%	43.18%	33.82%	27.85%	23.62%	20.40%	17.85%	15.77%	14.05%
Ks Ts	61.81%	44.88%	35.73%	30.02%	25.95%	22.93%	20.54%	18.61%	17.01%
Ks Th	59.73%	42.02%	32.54%	26.57%	22.41%	19.25%	16.80%	14.83%	13.22%
Ks 9s	60.01%	42.38%	33.07%	27.35%	23.37%	20.47%	18.22%	16.43%	14.99%
Ks 9h	57.81%	39.34%	29.61%	23.63%	19.57%	16.57%	14.26%	12.44%	10.95%
Ks 8s	58.31%	40.25%	30.92%	25.29%	21.49%	18.77%	16.67%	15.04%	13.72%
Ks 8h	56.01%	37.03%	27.27%	21.43%	17.53%	14.71%	12.57%	10.91%	9.58%
Ks 7s	57.52%	39.39%	30.07%	24.51%	20.81%	18.15%	16.13%	14.56%	13.28%
Ks 7h	55.20%	36.07%	26.33%	20.59%	16.75%	14.00%	11.95%	10.35%	9.10%
Ks 6s	56.66%	38.39%	29.17%	23.71%	20.15%	17.61%	15.65%	14.15%	12.92%
Ks 6h	54.21%	35.02%	25.37%	19.72%	16.03%	13.39%	11.43%	9.90%	8.71%
Ks 5s	55.80%	37.51%	28.41%	23.11%	19.63%	17.14%	15.28%	13.84%	12.66%
Ks 5h	53.29%	34.05%	24.54%	19.02%	15.44%	12.92%	11.02%	9.57%	8.42%
Ks 4s	54.88%	36.64%	27.68%	22.53%	19.15%	16.78%	14.97%	13.58%	12.45%
Ks 4h	52.33%	33.10%	23.73%	18.37%	14.90%	12.47%	10.68%	9.28%	8.18%
Ks 3s	54.05%	35.83%	26.99%	21.99%	18.74%	16.44%	14.68%	13.33%	12.26%
Ks 3h	51.43%	32.20%	22.98%	17.77%	14.43%	12.09%	10.36%	9.03%	7.96%
Ks 2s	53.20%	35.01%	26.35%	21.45%	18.34%	16.10%	14.45%	13.13%	12.08%
Ks 2h	50.50%	31.34%	22.24%	17.20%	13.98%	11.75%	10.11%	8.79%	7.79%
Qs Js	60.26%	44.30%	35.80%	30.31%	26.35%	23.30%	20.90%	18.96%	17.36%
Qs Jh	58.11%	41.46%	32.69%	27.05%	22.98%	19.86%	17.43%	15.45%	13.83%
Qs Ts	59.46%	43.23%	34.65%	29.19%	25.26%	22.36%	20.04%	18.19%	16.69%
Qs Th	57.30%	40.31%	31.43%	25.81%	21.81%	18.78%	16.42%	14.58%	13.07%
Qs 9s	57.66%	40.74%	31.99%	26.54%	22.75%	19.94%	17.75%	16.04%	14.68%
Qs 9h	55.37%	37.67%	28.55%	22.92%	19.04%	16.14%	13.93%	12.21%	10.81%
Qs 8s	56.02%	38.66%	29.84%	24.52%	20.85%	18.21%	16.19%	14.60%	13.34%
Qs 8h	53.61%	35.41%	26.23%	20.74%	16.99%	14.29%	12.22%	10.64%	9.39%
Qs 7s	54.30%	36.57%	27.86%	22.66%	19.21%	16.71%	14.84%	13.41%	12.22%
Qs 7h	51.76%	33.15%	24.07%	18.74%	15.18%	12.64%	10.75%	9.32%	8.18%
Qs 6s	53.62%	35.86%	27.15%	22.05%	18.65%	16.24%	14.45%	13.03%	11.92%
Qs 6h	51.02%	32.37%	23.29%	18.05%	14.57%	12.11%	10.28%	8.89%	7.82%
Qs 5s	52.77%	34.98%	26.40%	21.44%	18.16%	15.84%	14.10%	12.75%	11.69%
Qs 5h	50.12%	31.44%	22.50%	17.34%	14.00%	11.67%	9.92%	8.59%	7.55%
Qs 4s	51.87%	34.15%	25.72%	20.86%	17.72%	15.47%	13.82%	12.49%	11.47%
Qs 4h	49.14%	30.49%	21.73%	16.73%	13.49%	11.25%	9.58%	8.30%	7.32%
Qs 3s	51.02%	33.34%	25.06%	20.33%	17.29%	15.15%	13.54%	12.29%	11.28%
Qs 3h	48.23%	29.64%	21.01%	16.14%	13.03%	10.87%	9.29%	8.07%	7.11%
Qs 2s	50.17%	32.55%	24.42%	19.82%	16.91%	14.84%	13.29%	12.08%	11.11%
Qs 2h	47.31%	28.76%	20.29%	15.59%	12.61%	10.53%	9.02%	7.86%	6.94%
Js Ts	57.52%	42.05%	33.98%	28.75%	24.98%	22.13%	19.88%	18.13%	16.70%
Js Th	55.23%	39.16%	30.80%	25.45%	21.61%	18.69%	16.43%	14.64%	13.23%
Js 9s	55.62%	39.60%	31.35%	26.15%	22.50%	19.77%	17.67%	16.03%	14.72%
Js 9h	53.23%	36.50%	27.99%	22.64%	18.87%	16.09%	13.97%	12.35%	11.05%
Js 8s	54.02%	37.51%	29.23%	24.15%	20.64%	18.07%	16.12%	14.60%	13.39%
Js 8h	51.51%	34.26%	25.68%	20.46%	16.87%	14.24%	12.29%	10.79%	9.59%
Js 7s	52.31%	35.50%	27.27%	22.29%	18.95%	16.54%	14.70%	13.30%	12.20%
Js 7h	49.67%	32.07%	23.53%	18.43%	15.03%	12.57%	10.75%	9.38%	8.29%
Js 6s	50.60%	33.49%	25.40%	20.62%	17.44%	15.18%	13.53%	12.22%	11.20%
Js 6h	47.82%	29.92%	21.53%	16.60%	13.38%	11.12%	9.45%	8.19%	7.21%
Js 5s	49.98%	32.87%	24.83%	20.13%	17.04%	14.86%	13.21%	11.96%	10.95%
Js 5h	47.16%	29.27%	20.88%	16.06%	12.92%	10.73%	9.11%	7.89%	6.94%
Js 4s	49.07%	32.04%	24.13%	19.60%	16.59%	14.49%	12.92%	11.70%	10.74%
Js 4h	46.19%	28.36%	20.16%	15.46%	12.43%	10.34%	8.80%	7.63%	6.72%
Js 3s	48.24%	31.27%	23.50%	19.08%	16.21%	14.18%	12.67%	11.49%	10.57%
Js 3h	45.29%	27.48%	19.44%	14.89%	11.98%	9.95%	8.50%	7.40%	6.53%
Js 2s	47.36%	30.47%	22.86%	18.59%	15.82%	13.89%	12.45%	11.32%	10.42%
Js 2h	44.35%	26.63%	18.72%	14.34%	11.56%	9.65%	8.24%	7.18%	6.35%
Ts 9s	54.04%	38.90%	31.10%	26.09%	22.54%	19.89%	17.83%	16.26%	15.02%
Ts 9h	51.54%	35.81%	27.80%	22.66%	19.04%	16.33%	14.28%	12.74%	11.48%
Ts 8s	52.33%	36.83%	29.02%	24.13%	20.73%	18.21%	16.33%	14.87%	13.70%
Ts 8h	49.72%	33.58%	25.54%	20.51%	17.04%	14.52%	12.64%	11.21%	10.07%
Ts 7s	50.62%	34.79%	27.04%	22.30%	19.04%	16.68%	14.93%	13.55%	12.50%
Ts 7h	47.91%	31.40%	23.39%	18.50%	15.21%	12.84%	11.10%	9.78%	8.74%
Ts 6s	48.95%	32.85%	25.17%	20.56%	17.49%	15.26%	13.66%	12.38%	11.37%
Ts 6h	46.09%	29.29%	21.35%	16.65%	13.53%	11.31%	9.70%	8.48%	7.54%
Ts 5s	47.22%	30.94%	23.40%	19.01%	16.12%	14.07%	12.57%	11.38%	10.45%
Ts 5h	44.28%	27.25%	19.46%	15.00%	12.03%	10.02%	8.53%	7.42%	6.56%
Ts 4s	46.53%	30.35%	22.91%	18.60%	15.75%	13.75%	12.26%	11.12%	10.21%
Ts 4h	43.50%	26.58%	18.90%	14.48%	11.64%	9.66%	8.23%	7.15%	6.30%
Ts 3s	45.68%	29.58%	22.28%	18.10%	15.36%	13.45%	12.03%	10.93%	10.06%
Ts 3h	42.58%	25.76%	18.21%	13.94%	11.19%	9.31%	7.93%	6.90%	6.11%
Ts 2s	44.84%	28.82%	21.66%	17.61%	14.99%	13.16%	11.79%	10.74%	9.89%
Ts 2h	41.65%	24.93%	17.52%	13.40%	10.77%	9.00%	7.67%	6.70%	5.94%
9s 8s	50.78%	36.13%	28.61%	23.79%	20.40%	17.95%	16.09%	14.66%	13.53%
9s 8h	48.10%	32.87%	25.16%	20.21%	16.78%	14.30%	12.46%	11.06%	9.99%
9s 7s	49.11%	34.24%	26.81%	22.17%	18.97%	16.68%	14.97%	13.67%	12.63%
9s 7h	46.30%	30.83%	23.20%	18.46%	15.22%	12.93%	11.25%	9.98%	9.00%
9s 6s	47.44%	32.33%	24.96%	20.50%	17.48%	15.36%	13.75%	12.53%	11.54%
9s 6h	44.49%	28.76%	21.22%	16.64%	13.60%	11.45%	9.91%	8.74%	7.85%
9s 5s	45.72%	30.43%	23.22%	18.91%	16.07%	14.05%	12.56%	11.41%	10.50%
9s 5h	42.71%	26.73%	19.32%	14.92%	12.06%	10.07%	8.64%	7.55%	6.73%
9s 4s	43.87%	28.55%	21.52%	17.43%	14.76%	12.88%	11.51%	10.45%	9.59%
9s 4h	40.69%	24.70%	17.47%	13.31%	10.63%	8.80%	7.48%	6.50%	5.75%
9s 3s	43.26%	28.00%	21.05%	17.04%	14.43%	12.61%	11.27%	10.21%	9.39%
9s 3h	40.01%	24.10%	16.95%	12.88%	10.27%	8.48%	7.23%	6.26%	5.52%
9s 2s	42.44%	27.27%	20.46%	16.57%	14.07%	12.34%	11.04%	10.05%	9.23%
9s 2h	39.11%	23.28%	16.28%	12.35%	9.86%	8.18%	6.96%	6.07%	5.36%
8s 7s	47.93%	33.96%	26.80%	22.22%	19.10%	16.84%	15.17%	13.90%	12.87%
8s 7h	45.06%	30.58%	23.22%	18.57%	15.39%	13.16%	11.54%	10.29%	9.35%
8s 6s	46.27%	32.13%	25.11%	20.73%	17.78%	15.71%	14.17%	12.96%	12.03%
8s 6h	43.24%	28.62%	21.39%	16.94%	13.98%	11.92%	10.45%	9.32%	8.44%
8s 5s	44.54%	30.25%	23.36%	19.18%	16.39%	14.46%	13.01%	11.90%	11.01%
8s 5h	41.42%	26.59%	19.52%	15.25%	12.47%	10.57%	9.21%	8.17%	7.36%
8s 4s	42.71%	28.39%	21.66%	17.66%	15.00%	13.18%	11.83%	10.79%	9.96%
8s 4h	39.45%	24.57%	17.64%	13.59%	10.99%	9.20%	7.93%	6.99%	6.24%
8s 3s	40.86%	26.55%	19.99%	16.21%	13.78%	12.06%	10.81%	9.86%	9.06%
8s 3h	37.48%	22.58%	15.86%	12.04%	9.59%	8.00%	6.84%	5.96%	5.30%
8s 2s	40.27%	26.00%	19.56%	15.85%	13.46%	11.82%	10.60%	9.64%	8.89%
8s 2h	36.84%	22.00%	15.36%	11.62%	9.27%	7.69%	6.58%	5.74%	5.09%
7s 6s	45.36%	32.12%	25.24%	20.92%	18.02%	15.99%	14.49%	13.33%	12.39%
7s 6h	42.32%	28.62%	21.59%	17.19%	14.28%	12.28%	10.82%	9.74%	8.91%
7s 5s	43.69%	30.32%	23.62%	19.54%	16.84%	14.95%	13.56%	12.47%	11.58%
7s 5h	40.52%	26.71%	19.83%	15.69%	12.99%	11.15%	9.82%	8.84%	8.07%
7s 4s	41.84%	28.46%	21.94%	18.03%	15.49%	13.70%	12.41%	11.39%	10.58%
7s 4h	38.58%	24.70%	18.02%	14.04%	11.50%	9.81%	8.59%	7.67%	6.95%
7s 3s	40.00%	26.59%	20.24%	16.53%	14.13%	12.51%	11.26%	10.30%	9.51%
7s 3h	36.61%	22.68%	16.17%	12.43%	10.06%	8.47%	7.35%	6.52%	5.85%
7s 2s	38.16%	24.78%	18.63%	15.15%	12.93%	11.39%	10.26%	9.37%	8.65%
7s 2h	34.59%	20.71%	14.45%	10.91%	8.76%	7.30%	6.28%	5.53%	4.92%
6s 5s	43.13%	30.48%	23.88%	19.84%	17.19%	15.34%	13.97%	12.90%	12.01%
6s 5h	39.93%	26.87%	20.14%	16.04%	13.41%	11.59%	10.30%	9.31%	8.55%
6s 4s	41.32%	28.71%	22.33%	18.48%	16.02%	14.27%	13.04%	12.01%	11.20%
6s 4h	38.02%	24.97%	18.46%	14.56%	12.10%	10.48%	9.28%	8.39%	7.68%
6s 3s	39.52%	26.88%	20.66%	17.02%	14.68%	13.07%	11.90%	10.94%	10.18%
6s 3h	36.09%	22.97%	16.64%	12.99%	10.68%	9.15%	8.07%	7.24%	6.60%
6s 2s	37.67%	25.02%	19.02%	15.57%	13.38%	11.88%	10.77%	9.89%	9.15%
6s 2h	34.07%	20.98%	14.86%	11.40%	9.28%	7.85%	6.86%	6.11%	5.51%
5s 4s	41.46%	29.24%	22.87%	19.08%	16.61%	14.91%	13.62%	12.63%	11.77%
5s 4h	38.17%	25.56%	19.05%	15.19%	12.77%	11.13%	9.95%	9.06%	8.34%
5s 3s	39.70%	27.50%	21.33%	17.76%	15.49%	13.87%	12.71%	11.76%	10.98%
5s 3h	36.26%	23.68%	17.39%	13.78%	11.55%	10.04%	8.96%	8.13%	7.46%
5s 2s	37.86%	25.65%	19.71%	16.29%	14.17%	12.69%	11.58%	10.69%	9.95%
5s 2h	34.30%	21.69%	15.62%	12.20%	10.13%	8.77%	7.76%	6.99%	6.40%
4s 3s	38.66%	26.63%	20.58%	17.10%	14.88%	13.32%	12.20%	11.26%	10.48%
4s 3h	35.16%	22.78%	16.57%	13.07%	10.91%	9.44%	8.42%	7.62%	6.99%
4s 2s	36.83%	24.90%	19.07%	15.80%	13.75%	12.34%	11.27%	10.42%	9.70%
4s 2h	33.20%	20.89%	14.96%	11.67%	9.68%	8.39%	7.43%	6.72%	6.14%
3s 2s	36.00%	24.07%	18.34%	15.15%	13.19%	11.83%	10.80%	9.96%	9.27%
3s 2h	32.32%	19.99%	14.16%	10.99%	9.09%	7.84%	6.92%	6.23%	5.65%

Using multiple cores

In the "Calculating win odds" section, we showed that the conventional method for "As Ks" takes about 5 minutes on my laptop computer. However, modifying the code to support multiple cores is straightforward and yields some spectacular results.

	Single Thread (s)	Multiple Thread (s)	Speedup (X)
Single Core (w/Hyperthreading)	225.16	202.38	1.11
Dual Core	163.69	80.89	2.02
Quad Core	198.45	47.46	4.18
Dual Quad Core	171.91	21.26	8.09

The following code was used to benchmark the "Multiple Threads" column in the previous table. This example uses a thread pool to keep all of the cores "active." This technique is fairly straightforward to implement and the result is a roughly linear increase in speed based on the number of cores. I believe that the following example is fairly self-explanatory, but here are some of the highlights.

CalculateOdds() – This is a method that is the equivalent of the inner loop in the "Calculating win odds" example.
Main():
- Determines the number of opponent hands that we will feed to CalculateOdds; creates storage for each thread pool result.
- Creates a thread pool entry for each opponent hand using BeginInvoke. The IAsyncResult is held for this entry and used later to wait for and collect the results.
- Uses EndInvoke to wait for the thread items to complete and collects the results.
- Takes the results and calculates the odds using the same equations as in the "Calculating win odds" example. Note that the returned result is exactly the same.

using System;
using System.Collections.Generic;
using System.Runtime.InteropServices;
using System.Threading;
using HoldemHand;

namespace WinOddsMultipleThreads
{    
    class Program    
    {        
        // Holds Calculated Results
        public struct Results
        {
            public long win, ties, count;
        }

        // Delegate used in threadpool
        delegate Results CalculateOddsDelegate(
            ulong pocket, ulong opp, ulong board, ulong dead);

        // Method called and inserted in the threadpool
        static Results CalculateOdds(
            ulong pocket, ulong opp, ulong board, ulong dead)
        {
            // Initialize local results
            Results results = new Results();
            results.win = results.ties = results.count = 0;

            // Loop through all possible boards and tally the results
            foreach (
                ulong boardmask in Hand.Hands(board, dead | opp | pocket, 5))
            {
                uint playerHandval = Hand.Evaluate(pocket | boardmask, 7);
                uint oppHandval = Hand.Evaluate(opp | boardmask, 7);

                if (playerHandval > oppHandval)
                    results.win++;
                else if (playerHandval == oppHandval)
                    results.ties++;
                results.count++;
            }

            // Return tally 
            return results;
        }
        
        // Converts a hand iteration specification into an array of hands.
        static ulong [] HandList(ulong shared, ulong dead, int ncards)
        {
            List result = new List();

            foreach (ulong mask in Hand.Hands(shared, dead, ncards))
            {
                result.Add(mask);
            }
            return result.ToArray();
        }

        
        static void Main(string[] args)        
        {
            // This code calculates the probablity of As Ks winning against
            // another random hand.            
            ulong pocketmask = Hand.ParseHand("As Ks"); // Hole hand
            ulong board = Hand.ParseHand("");           // No board cards yet
            long wins = 0, ties = 0, count = 0;         
                // Iterate through all possible opponent hole cards            
            ulong [] opphands = HandList(0UL, board | pocketmask, 2); 
                // Create Array of Opponent Hands
            
            // Create delegate
            CalculateOddsDelegate d = 
                new CalculateOddsDelegate(CalculateOdds);

            // Create results array
            IAsyncResult[] results = new IAsyncResult[opphands.Length];

            // start time
            double start = Hand.CurrentTime;

            // Put calculation requests into the threadpool
            for (int i = 0; i < opphands.Length; i++)
            {
                results[i] = d.BeginInvoke(
                    pocketmask, opphands[i], 0UL, 0UL, null, null);
            }

            // Collect results once the threads have completed
            for (int i = 0; i < opphands.Length; i++)
            {
                Results r = d.EndInvoke(results[i]);
                wins += r.win;
                ties += r.ties;
                count += r.count;
            }

            // Prints: Win 67.0446323092352%            
            Console.WriteLine("Win {0}%, Elapsed Time {1}",
                (((double)wins) + ((double)ties) / 2.0) / (
                (double)count) * 100.0,
                Hand.CurrentTime-start);
        }
    }
}

Demo programs

I've included several demo programs and examples in the downloadable project. This is a quick summary of each of the demo applications:

Benchmark

The benchmark program tests the responsiveness of several aspects of the hand evaluator. Here is a list of the benchmark choices:

Evaluate() - Attempts to measure just the evaluation speed for each of the 9 hand types.
EvaluateType() - Attempts to measure the hand type evaluation method. This method doesn't return a complete hand value, but just returns the hand type. This method is faster than full hand evaluation.
Inline Iterations - Measures iteration of multiple hands using hand-coded iterators rather than IEnumerable.
C# Iterations - Measures iteration of multiple hands using IEnumerable C# iterators. This method is slower, but more understandable.
Evaluate/Iterate - Measures both C# Iterations and Evaluate().
Thread Pool Evaluate/Iterate - Measures C# Iterations and Evaluate() but does it in a way that utilized up to 16 cores. This can be used to see the relative improvement of Evaluate/Iterate when split across cores.

Multi-Odds

This application is similar to Hand Odds, but allows the number of random opponents to be selected. This application does not allow the Pocket Query Language to be used as arguments to the Pocket Hand and Opponent Hand input. That is an effort deferred for the future.

Acknowledgements

Wesley Tansey - For a lot of help with functions determining different variations of outs.
Matt Baker - For many discussions on outs and for providing the DiscountedOuts functions.
Scott Turner - For using and providing feedback on enhancements.
poker-eval - The core to my evaluation engine.
ZedGraph - I've used ZedGraph in several of the examples that graph results.
Malcolm Crowe - Author of the lexer generator/parser generator tools for C# that I used for the Pocket Query Language.

Licensing

This code is licensed using LGPL. See the comments in the source for more information. I use this license because it is the license referenced by the poker-eval code, which I use as my core evaluation engine.

Disclaimer

I could easily have spent another 6 months editing and tweaking the code and examples. I decided that I had spent enough time on this and had a "critical mass" of features available. So, here is my current code, warts and all.

I don't claim to be a great poker player or even a good one, for that matter. To paraphrase: those who can do, those who can't code. I don't recommend taking any poker advice I may have given (or implied to have given) in this article without independent verification.

I'd also like to encourage feedback. Poker programmers appear to be a somewhat secretive lot, for good reason I'm sure. I've learned a lot from the feedback I've been given over the last year or so. Please keep it coming.

History

First released May 2007

License

This article, along with any associated source code and files, is licensed under The GNU Lesser General Public License (LGPLv3)