Simple Ray Tracing in C#

• Download source - 3.3 KB
• Download binaries

 

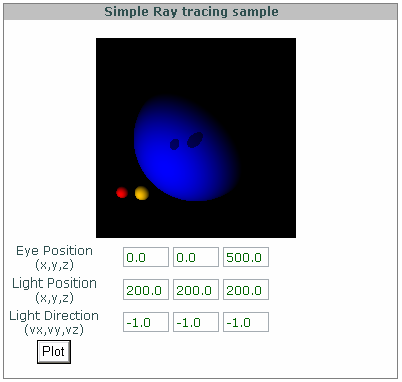
Introduction

This article demonstrates how to make a simple and very basic Ray Tracing with spheres; it can serve you as a base for implementing more complex algorithms. In a future article I will show how to improve this using image mapping.

Background

The Ray Tracing process is an approach to generate high quality computer graphics, as deeper the level of recursivity interaction with the 3D objects it has more photo realistic appearing.

The Ray Tracing Algorithm is implemented by calculating the intersection of 3D lines with the 3D objects in the model. The first point of the 3D line we define as the viewer position, the endpoint is located at the projection plane chosen. So for each discrete point at the projection plane an equation for the line is obtained and it is calculated all intersections with all objects selecting the intersection which are nearest to the viewer, so the color is plotted. Using this approach the implemented algorithm can handle opacity, light, shadows and so on.

 

Lines

3D lines equations can be represented in the form:

l = p + t * v

l = line

p = point in R³

t = scalar 

v = vector in R³

Or:

l_{(x,y,z) =} p_(x,y,z) + t * v_(x,y,z)

Where (p_x, p_y, p_z) are all the points lying in the 3D line, t is a scalar parameter, and (v_x, v_y, v_z) is a direction vector.

The above equation can also be obtained by the definition where a line can be defined by 2 points, so given two points P1 and P2 we have:

Point 1 P1(x1,y1,z1)

Point 2 P2(x2,y2,z2)

Vector v = P2-P1 = (x2-x1, y2-y1, z2-z1)

Replacing the vector v and p from the line equation l_{(x,y,z) =} p_(x,y,z) + t * v_(x,y,z) we have:

Line equation:

L(x) => x1 + t*(x2-x1)

L(y) => y1 + t*(y2-y1)

L(z) => z1 + t*(z2-z1)

So we can be sure that all (x,y,z) which satisfies the above equation belongs to the line defined by the points P1 and P2.

 

Spheres

Spheres can be represented in the form:

r2 = (x-cx)2+(y-cy)2+(z-cz)2

where

r is the sphere radius

(cx, cy, cz) is the center of the sphere

So we can be sure that all x,y,x points lie on the sphere surface.

Our objective now is to determine the intersection equation between a given line and a sphere it must be a set of (x,y,z) points which satisfies both equations. It is simple to imagine that a line versus a sphere intersection calculation can result in 0 intersections, 1 intersection (if tangent) or at most 2 intersections.

The Equations

In order to find if a line intersects a sphere and find the intersection, we do replace the x, y, and z from the line equation directly in the sphere equation.

So replacing x, y, and z we have:

Sphere equation r2 = (x-cx)2+(y-cy)2+(z-cz)2

Line equation

x = x1 + t*(x2-x1)

y = y1 + t*(y2-y1)

z = z1 + t*(z2-z1)

Replacing x,y and z gives:

r² = (x1 + t*(x2-x1)-cx)² + (y1 + t*(y2-y1) -cy)² + (z1+ t*(z2-z1)-cz)²

Let's create a variable for the vector:

vx = x2 - x1

vy = y2 - y1

vz = z2 - z1

So now we have:

r² = (x1-cx+t*vx)² + (y1-cy+t*vy)² + (z1-cz+t*vz)²

Let's replace (x1,y1,z1) with (px,py,pz) just to simplify...

(x1-cx+t*vx)² + (y1-cy+t*vy)² + (z1-cz+t*vz)² - r² = 0

Now we have a perfect 2nd-degree equation which can give us 0, 1 or 2 different solutions for 't' (and t gives us the intersection if there is):

a*t²+b*t+c = 0

a = (vx² + vy² + vz²)

b = 2.0 * (px * vx + py * vy + pz * vz - vx * cx - vy * cy - vz * cz)

c = px² - 2 * px * cx + cx² + py² - 2 * py * cy + cy² + pz² - 2 * pz * cz + cz² - r²

The intersection equation in C#

double A = (vx * vx + vy * vy + vz * vz);
double B = 2.0 * (px * vx + py * vy + pz * vz - vx * cx - vy * cy - vz * cz);
double C = px * px - 2 * px * cx + cx * cx + py * py - 2 * py * cy + cy * cy +
           pz * pz - 2 * pz * cz    + cz * cz - radius * radius;
double D = B * B - 4 * A * C;
double t = -1.0;
if (D >= 0)
     {
     double t1 = (-B - System.Math.Sqrt(D)) / (2.0 * A);
     double t2 = (-B + System.Math.Sqrt(D)) / (2.0 * A);
     if (t1 > t2)
          t = t1;
     else
          t = t2;  // we choose the nearest t from the first point
     }

The Source Code

<script language="C#" runat="server">
private void Page_Load(object sender, System.EventArgs e)
    {
    Bitmap newBitmap = new Bitmap(200, 200, PixelFormat.Format32bppArgb);
    Graphics g = Graphics.FromImage(newBitmap);

    Color clrBackground = Color.Black;
    g.FillRectangle(new SolidBrush(clrBackground), new Rectangle(0, 0, 200,
                    200));
    Rectangle rect = new Rectangle(0, 0, 200, 200);

    System.Collections.ArrayList obj3dArrayList;
    obj3dArrayList = new System.Collections.ArrayList();
    obj3dArrayList.Add(new Sphere(0.0, 0.0, 90.0, 100.0, 0.0, 0.0, 255.0));
    obj3dArrayList.Add(new Sphere(-180.0, -130.0, -110.0, 15.0, 255.0, 0.0,
                       0.0));
    obj3dArrayList.Add(new Sphere(-140.0, -140.0, -150.0, 20.0, 255.0, 200.0,
                       0.0));
    Graphics graphics = g;
    // viewer position
    double px = (double)Session["eyex"],
    py = (double)Session["eyey"],
    pz = (double)Session["eyez"];
    // light position
    double lpx = (double)Session["lpx"],
    lpy = (double)Session["lpy"],
    lpz = (double)Session["lpz"];
    // light direction
    double lvx = (double)Session["lvx"],
    lvy = (double)Session["lvy"],
    lvz = (double)Session["lvz"];
    double fMax = 200.0;
    for (int i = rect.Left; i <= rect.Right; i++)
        {
        double x = Sphere.GetCoord(rect.Left, rect.Right, -fMax, fMax, i);
        for (int j = rect.Top; j <= rect.Bottom; j++)
        {
            double y = Sphere.GetCoord(rect.Top, rect.Bottom, fMax, -fMax, j);
            double t = 1.0E10;
            double vx = x - px, vy = y - py, vz = -pz;
            double mod_v = Sphere.modv(vx, vy, vz);
            vx = vx / mod_v;
            vy = vy / mod_v;
            vz = vz / mod_v;
            bool bShadow = false;
            Sphere spherehit = null;
            for (int k = 0; k < (int)obj3dArrayList.Count; k++)
                {
                Sphere sphn = (Sphere)obj3dArrayList[k];
                double taux = Sphere.GetSphereIntersec(sphn.cx, sphn.cy,
                              sphn.cz,
                              sphn.radius, px, py, pz, vx, vy, vz);
                if (taux < 0) continue;
                if (taux > 0 && taux < t)
                {
                    t = taux;
                    spherehit = sphn;
                }
            }
            Color color = Color.FromArgb(10, 20, 10);
            if (spherehit != null)
            {
                double itx = px + t * vx, ity = py + t * vy, itz = pz +
                t * vz;
                // shadow
                double tauxla = Sphere.GetSphereIntersec(spherehit.cx,
                                spherehit.cy, spherehit.cz, spherehit.radius,
                                lpx, lpy, lpz, itx - lpx,
                                ity - lpy, itz - lpz);

                for (int k = 0; k < (int)obj3dArrayList.Count; k++)
                {
                    Sphere sphnb = (Sphere)(obj3dArrayList[k]);
                    if (sphnb != spherehit)
                    {
                        double tauxlb = Sphere.GetSphereIntersec(sphnb.cx,
                                        sphnb.cy, sphnb.cz, sphnb.radius, lpx,
                                        lpy, lpz, itx - lpx, ity - lpy, itz -
                                        lpz);
                        if (tauxlb > 0 && tauxla < tauxlb)
                        {
                            bShadow = true;
                            break;
                        }
                    }
                }
                double cost = Sphere.GetCosAngleV1V2(lvx, lvy, lvz, itx -
                              spherehit.cx, ity - spherehit.cy, itz -
                              spherehit.cz);
                if (cost < 0) cost = 0;
                double fact = 1.0;
                if (bShadow == true) fact = 0.5; else fact = 1.0;
                double rgbR = spherehit.clR * cost * fact;
                double rgbG = spherehit.clG * cost * fact;
                double rgbB = spherehit.clB * cost * fact;
                color = Color.FromArgb((int)rgbR, (int)rgbG, (int)rgbB);
                pen = new Pen(color);
            }
            Brush brs = new SolidBrush(color);
            graphics.FillRectangle(brs, i, j, 1, 1);
            brs.Dispose();

        }// for pixels lines
    }// for pixels columns
    ///////////////////////////////////////
    MemoryStream tempStream = new MemoryStream();
    newBitmap.Save(tempStream, ImageFormat.Png);
    Response.ClearContent();
    Response.ContentType = "image/png";
    Response.BinaryWrite(tempStream.ToArray());
    Response.Flush();
    }
</script>

The Sphere Class

public class Sphere
{
    public Sphere(double x, double y, double z, double r, double clr,
                  double clg, double clb)
    {
        cx = x;
        cy = y;
        cz = z;
        radius = r;
        clR = clr;
        clG = clg;
        clB = clb;
    }
    public static double GetCoord(double i1, double i2, double w1, double w2,
        double p)
    {
        return ((p - i1) / (i2 - i1)) * (w2 - w1) + w1;
    }
    public static double modv(double vx, double vy, double vz)
    {
        return System.Math.Sqrt(vx * vx + vy * vy + vz * vz);
    }
    void Move(double vx, double vy, double vz)
    {
        cx += vx;
        cy += vy;
        cz += vz;
    }
    void MoveTo(double vx, double vy, double vz)
    {
        cx = vx;
        cy = vy;
        cz = vz;
    }
    void RotX(double angle)
    {
        double y = cy * System.Math.Cos(angle) - cz * System.Math.Sin(angle);
        double z = cy * System.Math.Sin(angle) + cz * System.Math.Cos(angle);
        cy = y;
        cz = z;
    }
    void RotY(double angle)
    {
        double x = cx * System.Math.Cos(angle) - cz * System.Math.Sin(angle);
        double z = cx * System.Math.Sin(angle) + cz * System.Math.Cos(angle);
        cx = x;
        cz = z;
    }
    public static double GetSphereIntersec(double cx, double cy, double cz,
                         double radius, double px, double py, double pz,
                         double vx, double vy, double vz)
    {
        // x-xo 2 + y-yo 2 + z-zo 2 = r 2
        // x,y,z = p+tv
        // At2 + Bt + C = 0
        double A = (vx * vx + vy * vy + vz * vz);
        double B = 2.0 * (px * vx + py * vy + pz * vz - vx * cx - vy *
                   cy - vz * cz);
        double C = px * px - 2 * px * cx + cx * cx + py * py - 2 * py *
                   cy + cy * cy + pz * pz - 2 * pz * cz + cz * cz -
                   radius * radius;
        double D = B * B - 4 * A * C;
        double t = -1.0;
        if (D >= 0)
        {
            double t1 = (-B - System.Math.Sqrt(D)) / (2.0 * A);
            double t2 = (-B + System.Math.Sqrt(D)) / (2.0 * A);
            if (t1 > t2) t = t1; else t = t2;
        }
        return t;
    }
    public static double GetCosAngleV1V2(double v1x, double v1y, double v1z,
                                         double v2x, double v2y, double v2z)
    {
        /* incident angle
         intersection pt (i)
        double ix, iy, iz;
        ix = px+t*vx;
        iy = py+t*vy;
        iz = pz+t*vz;
        normal at i
        double nx, ny, nz;
        nx = ix - cx;
        ny = iy - cy;
        nz = iz - cz;

        cos(t) = (v.w) / (|v|.|w|)
        */
        return (v1x * v2x + v1y * v2y + v1z * v2z) / (modv(v1x, v1y, v1z) *
               modv(v2x, v2y, v2z));
    }
    public double cx, cy, cz, radius, clR, clG, clB;
}

 

Equations:

• x = px + t*vx
• y = py + t*vy
• z = pz + t*vz
• v = (x2-x1,y2-y1,z2-z1)
• x = x1 + t*(x2-x1)
• y = y1 + t*(y2-y1)
• z = z1 + t*(z2-z1)
• r2 = (x-cx)2+(y-cy)2+(z-cz)2
• r is the sphere radius
• (cx,cy,cz) is the center of the sphere
• r² = (x-cx)²+(y-cy)²+(z-cz)²
• x = x1 + t*(x2-x1)
• y = y1 + t*(y2-y1)
• z = z1 + t*(z2-z1)
• r² = (x1 + t*(x2-x1)-cx)² + (y1 + t*(y2-y1) -cy)² + (z1+ t*(z2-z1)-cz)²
• vx = x2 - x1
• vy = y2 - y1
• vz = z2 - z1
• r² = (x1-cx+t*vx)² + (y1-cy+t*vy)² + (z1-cz+t*vz)²
• (x1-cx+t*vx)² + (y1-cy+t*vy)² + (z1-cz+t*vz)² - r² = 0