Click here to Skip to main content
65,938 articles
CodeProject is changing. Read more.
Articles
 
(untagged)

Product Keys Based on Elliptic Curve Cryptography

0.00/5 (No votes)
5 Jun 2007 1  
A Near-optimal Product Key System Based on ECIES and Crypto++

Screenshot - image001.gif

Introduction

A popular method of product validation is using keys similar to VJJJBX-H2BBCC-68CF7F-2BXD4R-3XP7FB-JDVQBC. These compact keys can be derived using Public Key Cryptosystems such as Elliptic Curve Cryptography. Other Public Key Cryptosystems are available such as RSA. However, these systems generally produce larger keys, which the user will eventually have to enter into the program to unlock functionality. Smaller producing Cryptosystems exist, but it is the author's opinion that they are highly encumbered with patents. Quartz is one such example. It is a Public Key Encryption System that produces a smaller cipher text based on Hidden Field Equations (HFEs). The Quartz website is littered with phrases such as "must license" and "pay royalties".

The reader is also encouraged to investigate Signature Schemes with Recovery as an alternative method to producing Product Keys. An example is PSS-R, a Message Recovery Signature Scheme based on RSA. PSS-R is not suitable for product keys due to the size of the resulting key. However, cryptosystems such as a Weil Pairing system should be of interest. Once Weil Pairing is finalized in committee, it will be added to the Crypto++ library.

Finally, the reader should also visit Product Keys Based on the Advanced Encryption Standard to familiarize themselves with basic concepts of Product Keys in the domain of Public Key Cryptography; and Product Activation Based on RSA Signatures. This article will discuss in detail the following topics:

  • Elliptic Curve Cryptography Implementation in Crypto++
  • Using Elliptic Curves with User Defined Domain Parameters In Crypto++
  • Base Encoding a cipher text String in Crypto++
  • Working Demo which Exercises Product Keys based on ECC
  • Bulk Product Key Generation
  • Product Key Validation
  • Product Activation
  • Securely Saving Key or Activation State to the Registry

This article is based on the Visual C++ 6.0 Environment in hopes that it reaches the largest audience. There are 16 downloads available with this article, which are presented at the top of the page.

Elliptic curve cryptography

This article assumes that the reader has a basic understanding of Cryptography. For an overview, see Gary Kessler's An Overview of Cryptography. For an ECC Tutorial, see Certicom's ECC Tutorial. For a casual Cryptography reader, Elliptic Curve Cryptography should prove to be interesting, as it is not like RSA (based on Integer Factorization), Diffie-Hellman and ElGamal (based on Discrete Logarithms), or MQ (Multivariate Quadratics). However, ECC is related to DLP. This article uses comparatively small EC key sizes. This is justified in that the Product Key lifetime is relatively short, based directly on Product Life Cycles. RSA Laboratories offers the following recommendations for key sizes:

Protection Lifetime
of Data

Present � 2010

Present � 2030

Present � Beyond 2031

Minimum Symmetric Security Level

80 bits

112 bits

128 bits

Minimum RSA
Key Size

1024 bits

2048 bits

3072 bits

Below is a comparison of the equivalent Key sizes of ECC and RSA.

The following Figure estimates the Security Level of ECC and RSA & DSA in MIPS Years.

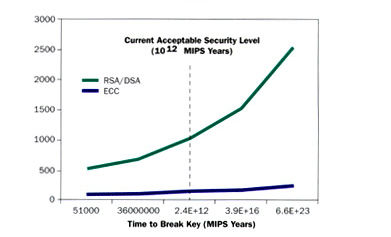
The friendly folks at the US Government's NSA have put together some reading that may also be of interest. The article is titled The Case for Elliptic Curve Cryptography. It is very noteworthy that Peter Shor of AT&T Research has a Quantum Factoring Algorithm, which runs in O((log n)3) time. Additionally, Shor has proposed a Quantum Root Finding Algorithm that is also polynomial in time complexity (to solve the Discrete Logarithm problem). In 2001, IBM built a quantum computer capable of factoring the number 15 (using 7 qubits - the quantum equivalent of 27) using Shor's Algorithm. It is believed the future will produce quantum computers with over 1000 qubits. Finally, J. E. Cremona has published his book Algorithms for Modular Elliptic Curves online.

Compiling and integrating Crypto++

Please see the related article, Compiling and Integrating Crypto++ into the Microsoft Visual C++ Environment. This article is based upon basic assumptions presented in the previously mentioned article. It also addresses most problems encountered with projects from Command Line to MFC (Errors C1083, C1189, LNK1104, LNK2001, and LNK2005). Additionally, it provides tips and other niceties for using the Crypto++ Library.

Elliptic curve cryptography implementation in Crypto++

Crypto++ can be an intimidating library at times. The author finds the easiest method for getting a user started is by giving him or her a working CLI project. Multiple projects are presented with this article. They simply exercise the Crypto++ ECC Implementation on the command line. The samples build upon one another until a fully implemented demo is presented. The author chose this method because two of his favorite authors use it - Jeffrey Richter and W. Richard Stevens. The first sample should be considered ecctest160. ecc160test uses an Elliptical Curve over a 160 bit field. This is the equivalent of 1024 RSA moduli, or an 80 bit Symmetric Key. Some notes on the code below:

  • CryptoPP::AutoSeededRandomPool rng contructs a Cryptographically Secure Pseudo-random Number Generator which is auto-seeded
  • unsigned int PlainTextLength = PlainText.length() + 1 is used to capture the trailing '\0' of the string
  • std::basic_string::c_str() is guaranteed to offer the trailing '\0' whereas std::basic_string::data() is not
  • The try and various catch() statements have been omitted for clarity
  • The throw std::string is present because a 0 length indicates an abnormal condition from the Crypto++ library
  • The author prefers not to pollute the Global Namespace, so objects are brought in with the scope operator: std::string and CryptoPP::ECIES< CryptoPP::ECP >::PrivateKey rather than issuing using namespace std or using namespace CryptoPP 
// From ecctest160


CryptoPP::ECIES< CryptoPP::ECP >::PrivateKey    PrivateKey;
CryptoPP::ECIES< CryptoPP::ECP >::PublicKey     PublicKey;
CryptoPP::AutoSeededRandomPool                  rng;

    // Curve and Key Initialization

    PrivateKey.Initialize( rng, CryptoPP::ASN1::secp160r1() );
    PrivateKey.MakePublicKey( PublicKey );

    // Key Validation

    //   Level 3 Validation (not 3 rounds)

    if( false == PrivateKey.Validate( rng, 3 ) )
    { 
        throw std::string( "Private Key Validation  Error"); 
    }
    if( false == PublicKey.Validate( rng, 3 ) )
    { 
        throw std::string( "Public Key Validation Error" ); 
    }

    // Encryptor and Decryptor

    CryptoPP::ECIES< CryptoPP::ECP >::Encryptor Encryptor( PublicKey );
    CryptoPP::ECIES< CryptoPP::ECP >::Decryptor Decryptor( PrivateKey );

    // Message

    std::string PlainText = "Yoda said, Do or do not. There is no try.";

    // Runtime Sizes...

    unsigned int PlainTextLength = PlainText.length() + 1;
    unsigned int CipherTextLength =
        Encryptor.CiphertextLength( PlainTextLength );
    if( 0 == CiphertextLength ) 
    { 
        throw std::string("plaintextLength is not valid (too long)"); 
    }

    // Scratch for Encryption

    byte* CipherText = new byte[ CipherTextLength ];

    // Encryption

    Encryptor.Encrypt( rng, reinterpret_cast<const byte*>
        ( PlainText.c_str() ), PlainTextLength, CipherText );

    // Scratch for Decryption

    unsigned int RecoveredTextLength =
        Decryptor.MaxPlaintextLength( CipherTextLength );
    if( 0 == RecoveredTextLength )
    { 
        throw std::string(
            "CipherTextLength is not valid (too long or too short)"); 
    }

    // Decryption Buffer

    char* RecoveredText = new char[ RecoveredTextLength ];

    // Decryption

    Decryptor.Decrypt( rng, CipherText, CipherTextLength,
        reinterpret_cast<byte*>( RecoveredText ) );

ecctest1 is a generalization of ecc160test. One can choose odd characteristic fields of Fp (where p>3 is a large prime) by #define ECC_FIELD CryptoPP::ECP for curves from 112 bits to 521 bits; and fields of characteristic two (F2^m) for curves from 113 bits to 571 bits by #define ECC_FIELD CryptoPP::EC2N.

// From ecctest1


#define ECC_FIELD CryptoPP::ECP
// #define ECC_FIELD CryptoPP::EC2N


// Standard ECC Curves over GF(p)

//   Use when ECC_FIELD is CryptoPP::ECP

//

// #define ECC_CURVE CryptoPP::ASN1::secp112r1()

// #define ECC_CURVE CryptoPP::ASN1::secp112r2()

...
#define ECC_CURVE CryptoPP::ASN1::secp160r1()
...
// #define ECC_CURVE CryptoPP::ASN1::secp384r1()

// #define ECC_CURVE CryptoPP::ASN1::secp521r1()



// ECC Curves over GF(2)

//   Use when ECC_FIELD is CryptoPP::EC2N

//

// #define ECC_CURVE CryptoPP::ASN1::sect113r1()

// #define ECC_CURVE CryptoPP::ASN1::sect113r2()

...
// #define ECC_CURVE CryptoPP::ASN1::sect571k1()

// #define ECC_CURVE CryptoPP::ASN1::sect571r1()


int main(int argc, char* argv[]) {

    CryptoPP::ECIES< ECC_FIELD >::PrivateKey    PrivateKey;
    CryptoPP::ECIES< ECC_FIELD >::PublicKey     PublicKey;
    CryptoPP::AutoSeededRandomPool              rng;

    // Curve Key Generation

    PrivateKey.Initialize( rng, ECC_CURVE );
    PrivateKey.MakePublicKey( PublicKey );
    
    // Encryptor and Decryptor

    CryptoPP::ECIES< ECC_FIELD >::Encryptor Encryptor( PublicKey );
    CryptoPP::ECIES< ECC_FIELD >::Decryptor Decryptor( PrivateKey );

    ...

    return 0;
}

Using elliptic curves with user-defined domain parameters in Crypto++

Crypto++ supplies 31 predefined Elliptical Curves for use with ECIES (Elliptic Curve Integrated Encryption Scheme) as specified in ANSI X9.63. These curves range in size from 112 bits to 571 bits. Encrypting a 4 byte message with a 112 bit ECIES object produces a cipher text length of 53 bytes. Encrypting the same message with an ECIES object of 34 bits will produce a 35 byte cipher text. The large cipher text is due in part to the following: when using Crypto++, a CryptoPP::ECIES< CryptoPP::ECP > object is created. The CryptoPP::ECIES< CryptoPP::ECP >::Encryptor returns a cipher text object which is a tuple (V, C, T) consisting of the following components:

  • temporary EC public key V
  • encrypted message C
  • authentication tag T (generated from message M)

It is very noteworthy that public key V is a temporary key. This provides a randomization of the Product Key. However, should the reader's binary fall to Reverse Engineering, a private key is compromised due to the decryption routine. The authentication tag T is derived from SHA-1. The SHA-1 block size is 160 bits. So the authentication tag accounts for approximately 160/8 or approximately 20 bytes of the cipher text object. The astute reader should realize another benefit of a Signature Scheme with Message Recovery at this point. More will follow later in this article with respect to authentication tag T paring. Ideally, the cipher text will be about 20 bytes. This will produce a key of 30 to 35 characters in length after Base Encoding the cipher text into a Product Key. Again, further reductions will be achieved later in the article.

Using elliptic curve builder to generate domain parameters

For this portion of the article, Elliptic Curve Builder (ECB) will be used to generate curves for use with the Product Keys. Many thanks to Marcel Martin for modifying his original Object Pascal code to accommodate this article. ECB can be downloaded here. A copy of the ECB version 1.0.0.6 is not included with the article. However, it is obtainable from Marcel's Ellipsa page. The author chose to use ECB rather than implementing a curve parameter generator due to the difficulty in determining the order of E(Fp). For reading on the subject, begin with 'Schoof-Atkin-Elkies Algorithm' and 'Elliptic Curve Point Counting Algorithm'.

Open ECB and click the leftmost blue thunderbolt. This will generate new curve parameters over Fp.

In the New Curve Parameters Over... Dialog Box, enter the following:

  • Suitable Curve Size (minimum is 33 bits)
  • Cofactor S max binary size of 2

A note on EC Domain Parameters and ECB: although the ECB editor displays Discriminant as 0, ECB begins its search at Discriminant + 1, so the parameter does not require modification. The ECB Discriminant value is for Complex Multiplication. This is a different Discriminant than that of Weierstrass equation of y2 ≡ x3 + ax + b (mod p). A non-0 Discriminant is required for the later case in this Cryptosystem. Eventually, Crypto++ will check the condition 4a3 + 27b2 !≡ 0 (mod p). For a complete list of required checks, see Certicom's accompanying document, SEC 1: Elliptic Curve Cryptography. Section 3.1.1.1, Elliptic Curve Domain Parameters over Fp Generation Primitive, is the appropriate area of the document.

Cofactor S max binary size is set to 2 because 22 = 4. According to the Certicom document, h ≤ 4 (S in ECB, h in EC literature). If the reader is inclined, a larger S can be selected. Marcel recommends at least 3, so a cofactor of 4 is available. If the user encounters cofactor S of 5, 6, or 7, he or she should regenerate the parameters. Note that NIST predefined curves specify a cofactor h = 1, 2, or 4 to speed calculations. Certicom requires that CEIL(log2p) = {112, 128, 160, 192, 224, 256, 384, 521} for E(Fp). At this point, the article is well below the recommended minimum curve size of 112 bits for E(Fp). Use of E(Fp) 56 bit curves will be presented later in the article. A 56 bit curve is available for E(F2^m). The exercise is left to the reader.

Next, select the tab entitled "Curve and Point." Click the yellow thunderbolt. The presented parameters are acceptable. Note that NIST curves use A = -3 to speed underlying mathematical operations.

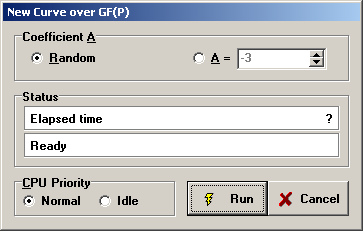
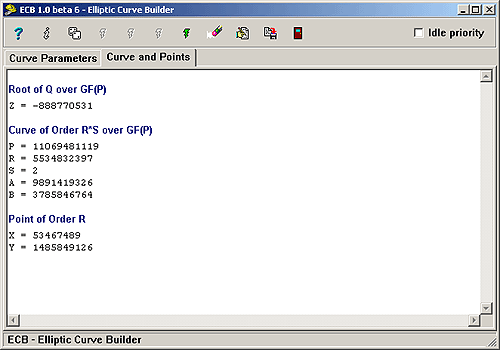
Finally, click the green thunderbolt in the editor. This will produce G(x, y) points of Order R over the Curve E(Fp). Note that negative values are acceptable for either a, b, x or y. However, SEC1, Section 3.1.1.2.1 Elliptic Curve Domain Parameters over Fp Validation Primitive (check 2) states:

Check that a, b, xG, and yG are integers in the interval [0, p-1].

To facilitate the requirement, issue the following:

    // parameters are in the interval [0, p-1]

    a %= p; b %= p; x %= p; y %= p;

Copy and Paste the parameters into Visual C++ to avoid transcription errors.

ecctest2 exercises Crypto++ and the User Defined Domain Parameters. The essence of ecctest2 is below, as well as some notes:

  • p, a, and b define the curve
  • Base Point G is specified as a (x,y) coordinate 
// From ecctest2


// Crypto++ Includes

#include "cryptlib.h"

#include "osrng.h"      // Random Number Generator

#include "eccrypto.h"   // Elliptic Curve

#include "ecp.h"        // F(p) EC

#include "integer.h"    // Integer Operations

int main(int argc, char* argv[]) {

    CryptoPP::AutoSeededRandomPool rng;

    // User Defined Domain Parameters

    CryptoPP::Integer p("11069481119");
    CryptoPP::Integer a("9891419326");
    CryptoPP::Integer b("3785846764");
    CryptoPP::Integer n("5534832397");          // R from ECB

    CryptoPP::Integer h("2");                   // S from ECB, must be <= 4

    CryptoPP::Integer x("53467489");
    CryptoPP::Integer y("1485849126");
    CryptoPP::ECP ec( p, a, b );
    CryptoPP::ECP::Point G( x, y );
    CryptoPP::ECIES< CryptoPP::ECP >::PrivateKey    PrivateKey;
    CryptoPP::ECIES< CryptoPP::ECP >::PublicKey     PublicKey;

    // Curve Initialization and Key Generation

    PrivateKey.Initialize( ec, G, n, h );
    PrivateKey.MakePublicKey( PublicKey );

    // Encryptor and Decryptor

    CryptoPP::ECIES< CryptoPP::ECP >::Encryptor Encryptor( PublicKey );
    CryptoPP::ECIES< CryptoPP::ECP >::Decryptor Decryptor( PrivateKey );
   
    // Message

    std::string PlainText = " ECC ";

    // Runtime Sizes...

    unsigned int PlainTextLength = PlainText.length() + 1;
    unsigned int CipherTextLength =
        Encryptor.Cipher=CiphertextLength( PlainTextLength );
    if( 0 == CiphertextLength )
    { 
        throw std::string("PlainTextLength is not valid (too long)"); 
    }

    // Scratch for Encryption

    byte* CipherText = new byte[ CipherTextLength ];

    // Encryption

    Encryptor.Encrypt( 
        rng, reinterpret_cast<const byte*>( PlainText.c_str() ),
        PlainTextLength, CipherText );

    // Scratch for Decryption

    unsigned int RecoveredTextLength =
        Decryptor.MaxPlaintextLength( CipherTextLength );
    if( 0 == RecoveredTextLength )
    { 
        throw std::string(
            "CipherTextLength is not valid (too long or too short)"); 
    }

    // Decryption Buffer

    char* RecoveredText = new char[ RecoveredTextLength ];

    // Decryption

    Decryptor.Decrypt( rng, CipherText, CiphertextLength,
        reinterpret_cast<byte*>( RecoveredText ) );

    // Diagnostics

    std::cout << "Recovered text (
        " << RecoveredTextLength << " bytes):" << std::endl;
    std::cout << "'" << RecoveredText << "'" << std::endl;

    return 0;
}

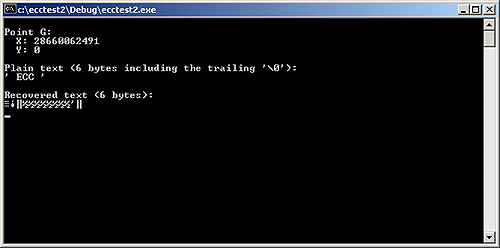
Below is a sample output with satisfactory parameters. The litmus test is definitive: the message decrypts.

Finally, I'll discuss a sample output with unsatisfactory parameters. Should a reader encounter similar, perform the following:

  • Verify ECB parameters were correctly transcribed
  • Generate new parameters with ECB.

Encoding a cipher text string in Crypto++

For encoding and decoding of the cipher text, this article will use both the Crypto++ base 64 encoder and base 32 encode. Better alphabet choices exist for Product Keys. For example, the following is a short list of alphabet constraints for Product Keys

  • Key are formed over the alphabet A-Z and 0-9
  • Keys are not case sensitive
  • Do not use letters l (lowercase "L") or O (capital "o") (appear as numbers in some fonts)
  • Do not use letters u and v (appear similar in some fonts)
  • Do not use numbers 0 or 1 (appear as letters in some fonts)
  • Print keys using a font created for text scanning (it is easier to distinguish characters)

Base Encoding expansion for Base64 encoding is approximately 35%, while expansion for Base32 encoding is approximately 60%. These estimates are based on a psuedo-randomly generated block of 16 * 1024 (16384) bytes. See the accompanying BaseExp for the program used to generate the sample block and calculate the expansions.

// From ecctest3


// Crypto++ Includes

#include "cryptlib.h"

#include "osrng.h"      // Random Number Generator

#include "eccrypto.h"   // Elliptic Curve

#include "ecp.h"        // F(p) EC

#include "integer.h"    // Integer Operations

#include "base64.h"     // Base 64 Encode/Decoder


int main(int argc, char* argv[]) 
{
    // User Defined Domain Parameters Omitted

    // ec, G, n, h


    CryptoPP::ECIES< CryptoPP::ECP >::PrivateKey    PrivateKey;
    CryptoPP::ECIES< CryptoPP::ECP >::PublicKey     PublicKey;

    PrivateKey.Initialize( ec, G, n, h );
    PrivateKey.MakePublicKey( PublicKey );

    // Encryptor and Decryptor

    CryptoPP::ECIES< CryptoPP::ECP >::Encryptor Encryptor( PublicKey );
    CryptoPP::ECIES< CryptoPP::ECP >::Decryptor Decryptor( PrivateKey );

    // Message

    std::string PlainText = " ECC ";

    // Runtime Sizes...

    unsigned int PlainTextLength = PlainText.length() + 1;
    unsigned int CipherTextLength = Encryptor.CiphertextLength( 
        PlainTextLength );
    if( 0 == CipherTextLength )
    { 
        throw std::string("plaintextLength is not valid (too long)"); 
    }

    // Scratch for Encryption

    byte* CipherText = new byte[ CipherTextLength ];

    // Encryption

    Encryptor.Encrypt( 
        rng, reinterpret_cast<const byte*>( PlainText.c_str() ),
        PlainTextLength, CipherText );

    // Base 64 Encoding

    CryptoPP::Base64Encoder Encoder;
    Encoder.Put( CipherText, CipherTextLength );
    Encoder.MessageEnd();

    // Scratch for Base 64 Encoded cipher text

    unsigned int EncodedTextLength = Encoder.MaxRetrievable();
    byte* EncodedText = new byte[ EncodedTextLength + 1 ];   
        // + 1 for NULL termination

    EncodedText[ EncodedTextLength ] = '\0';                
        // NULL Terminate


    // Base 64 Encoded cipher text

    Encoder.Get( EncodedText, EncodedTextLength );

    // Base 64 Decoding

    CryptoPP::Base64Decoder Decoder;
    Decoder.Put( EncodedText, EncodedTextLength );
    Decoder.MessageEnd();

    // Scratch for Base 64 Decoded cipher text

    unsigned int DecodedTextLength =  Decoder.MaxRetrievable();
    byte* DecodedText = new byte[ DecodedTextLength ];

     // cipher text is no longer Encoded 

    Decoder.Get( DecodedText, DecodedTextLength );

    // At this point, DecodedText = CipherText

    //   assert( DecodedTextLength == CiphertextLength );

    assert( 0 == ::memcmp( DecodedText, CipherText, CiphertextLength ) );

    // Scratch for Decryption

    unsigned int RecoveredTextLength = Decryptor.MaxPlaintextLength( 
        CiphertextLength );
    if( 0 == RecoveredTextLength )
    { 
        throw std::string(
            "CiphertextLength is not valid (too long or too short)"); 
    }

    // Decryption Buffer

    char* RecoveredText = new char[ RecoveredTextLength ];
    // Decryption

    Decryptor.Decrypt( rng, CipherText, CipherTextLength,
        reinterpret_cast<byte*>( RecoveredText ) );

     // Diagnostics

    std::cout << "Recovered text (
        " << RecoveredTextLength << " bytes):" << std::endl;
    std::cout << "'" << RecoveredText << "'" << std::endl;
}

ecctest3 is the driver for this portion of the article - Base64 encoding the cipher text. The results of running ecctest3 should be similar to below.

Product keys based on ECC

This (near anticlimactic) portion of the article discusses Feature Encoding. ecctest4.zip is the sample archive. Feature Encoding requires very few bytes. In the author's sample it is 4 bytes, as one unsigned int is used. Other notes on the code are:

  • Message is now an unsigned int rather than a std::string
  • Features is a bit mask values
  • Magic is the final check to verify the Product Key is Valid 
// From ecctest4


// The Features Available...

const unsigned int FEATURE_EVALUATION  = 0x01;  // 0000 0001

const unsigned int FEATURE_USE_SQUARES = 0x02;  // 0000 0010

const unsigned int FEATURE_USE_CIRCLES = 0x04;  // 0000 0100

const unsigned int FEATURE_USE_WIDGETS = 0x08;  // 0000 1000


 // 1010 1010 1010 1010 0000 0000 0000 0000

const unsigned int FEATURE_MAGIC = 0xAAAA << 16;

 // 1111 1111 1111 1111 0000 0000 0000 0000

const unsigned int FEATURE_MAGIC_MASK = 0xFFFF << 16;

int main(int argc, char* argv[]) 
{
    // User Defined Domain Parameters Omitted

    // ec, G, n, h

    CryptoPP::ECIES< CryptoPP::ECP >::PrivateKey    PrivateKey;
    CryptoPP::ECIES< CryptoPP::ECP >::PublicKey     PublicKey;
   
    PrivateKey.Initialize( ec, G, n, h );
    PrivateKey.MakePublicKey( PublicKey );

    // Encryptor and Decryptor

    CryptoPP::ECIES< CryptoPP::ECP >::Encryptor Encryptor( PublicKey );
    CryptoPP::ECIES< CryptoPP::ECP >::Decryptor Decryptor( PrivateKey );

    // Message

    unsigned int Features = 0;
    Features |= FEATURE_MAGIC;
    Features |= FEATURE_USE_WIDGETS;
    Features |= FEATURE_USE_SQUARES;

    // Runtime Sizes...

    unsigned int PlainTextLength = sizeof( Features );
    unsigned int CipherTextLength = Encryptor.CiphertextLength( 
        PlainTextLength );
    if( 0 == CipherTextLength )
    { 
        throw std::string("PlainTextLength is not valid (too long)"); 
    }

    // Scratch for Encryption

    CipherText = new byte[ CipherTextLength ];

    // Encryption

    Encryptor.Encrypt( rng, reinterpret_cast<const byte*>( &Features ),
        PlainTextLength, CipherText );

    // Base 64 Encoding

    CryptoPP::Base64Encoder Encoder;
    Encoder.Put( CipherText, CipherTextLength );
    Encoder.MessageEnd();

    // Scratch for Base 64 Encoded cipher text

    unsigned int EncodedTextLength = Encoder.MaxRetrievable();
    EncodedText = new byte[ EncodedTextLength + 1 ];
    EncodedText[ EncodedTextLength ] = '\0';

    // Fetch Base 64 Encoded cipher text

    Encoder.Get( EncodedText, EncodedTextLength );

    // Diagnostics...

    std::cout << "Encoded Text Before Tampering:" << 
        std::endl << EncodedText << std::endl;

    // Output

    if( FEATURE_EVALUATION  == (Features & FEATURE_EVALUATION ) )
    { 
        std::cout << "Evaluation Edition." << std::endl; 
    }
    if( FEATURE_USE_SQUARES == (Features & FEATURE_USE_SQUARES) )
    { 
        std::cout << "Operations are permitted on Squares." << std::endl; 
    }
    if( FEATURE_USE_CIRCLES == (Features & FEATURE_USE_CIRCLES) )
    { 
        std::cout << "Operations are permitted on Circles." << std::endl; 
    }
    if( FEATURE_USE_WIDGETS == (Features & FEATURE_USE_WIDGETS) )
    { 
        std::cout << "Operations are permitted on Widgets." << std::endl; 
    }
    std::cout << std::endl << "********************" << 
        std::endl << std::endl;

    // The folllowing introduces multiple random errors

    // Simulate guessing at a Product Key

    char ch = 'A';
    for( unsigned int i = 0; i < EncodedTextLength - 1; i += 3 )
    { 
        EncodedText[ i ] = ch++; 
    }

    // Diagnostics...

    std::cout << "Encoded Text After Tampering:" << std::endl << 
        EncodedText << std::endl;
   
    // Base 64 Decoding

    CryptoPP::Base64Decoder Decoder;
    Decoder.Put( EncodedText, EncodedTextLength );
    Decoder.MessageEnd();

    // Scratch for Base 64 Decoded cipher text

    unsigned int DecodedTextLength = Decoder.MaxRetrievable();
    DecodedText = new byte[ DecodedTextLength ];

    // Fetch Base 64 Decoded cipher text

    Decoder.Get( DecodedText, DecodedTextLength );

    // Scratch for Decryption

    unsigned int RecoveredTextLength = Decryptor.MaxPlaintextLength( 
        DecodedTextLength );
    if( 0 == RecoveredTextLength )
    { 
        throw std::string(
            "CipherTextLength is not valid (too long or too short)"); 
    }

    // Decryption Buffer

    unsigned int RecoveredText = static_cast<int>( -1 );    // 1111 ... 1111


    // Decryption

    Decryptor.Decrypt( rng, DecodedText, DecodedTextLength,
        reinterpret_cast<byte *>( &RecoveredText ) );

    // Output

    if( FEATURE_MAGIC != (RecoveredText & FEATURE_MAGIC_MASK ) )
    {
        throw( std::string("Invalid Product Key!") );
    }

    else
    {
        if( FEATURE_EVALUATION  == (RecoveredText & FEATURE_EVALUATION ) )
        { 
            std::cout << "Evaluation Edition." << std::endl; 
        }
        if( FEATURE_USE_SQUARES == (RecoveredText & FEATURE_USE_SQUARES) )
        { 
            std::cout << "Operations are permitted on Squares." << std::endl; 
        }
        if( FEATURE_USE_CIRCLES == (RecoveredText & FEATURE_USE_CIRCLES) )
        { 
            std::cout << "Operations are permitted on Circles." << std::endl; 
        }
        if( FEATURE_USE_WIDGETS == (RecoveredText & FEATURE_USE_WIDGETS) )
        { 
            std::cout << "Operations are permitted on Widgets." << std::endl; 
        }
    }
    return 0;
}

Results from running ecctest4 are shown below. ecctest4 Base64 encodes a Feature bit value rather than a string.

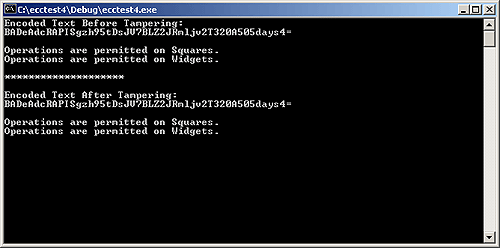
ecctest5 Base32 encodes the Features and formats the key.

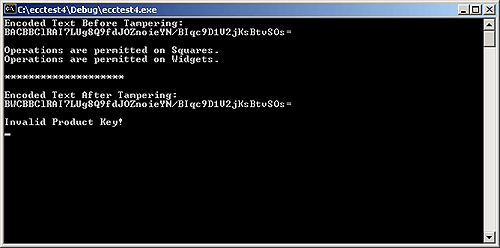
The output above displays the execution of ecctest5. ecctest5 adds the following, shown in the code example below:

  • Base 32 Encoding
  • 'Pretty Printing' of the Base 32 Encoded cipher text
  • Use of CryptoPP::DecodingResult to detect altered Product Keys 
// From ecctest5


// Base 32 Encoding

CryptoPP::Base32Encoder Encoder;
Encoder.Put( CipherText, CipherTextLength );
Encoder.MessageEnd();

    ...

    // Pretty Print

    const unsigned int BREAK = 7;
    for(unsigned int i = 0; i < EncodedTextLength; i++)
    {
        if( 0 != i && 0 == i % BREAK )
        { 
            std::cout << "-"; 
        }
        std::cout << EncodedText[ i ];
    };
    std::cout << std::endl;

    ...

    // Decryption

    CryptoPP::DecodingResult Result =
        Decryptor.Decrypt( rng, DecodedText, DecodedTextLength,
        reinterpret_cast<byte *>( &RecoveredText ) );

    // Crypto++ Test

    if( false == Result.isValidCoding )
    { 
        throw std::string("Crypto++: Invalid Coding"); 
    }

To further reduce the size of the Product Key, this article creates a spurious authentication tag T for the cipher text object (C,V,T). Ideally, a 0 byte HMAC function would have been added to CryptoPP::DL_EncryptionAlgorithm_Xor(...). However, Microsoft's environment could not properly generate code with arrays of size 0. SecByteBlock<> caused too many C2229 compilations. errors.

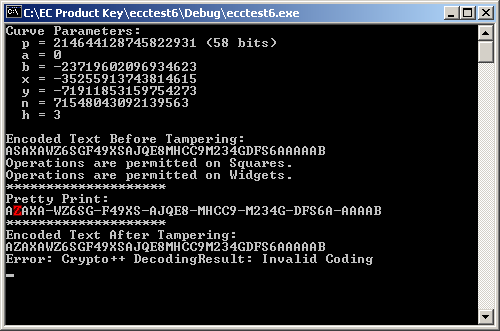
As a compromise, TRUEHash was created. The hash returns the same value regardless of the message - 0x01. TRUEHash adds approximately 4 bytes of authentication tagging, T in the cipher text Object (C,V,T). Template specialization for TRUEHash is below. Note also the curve size is 58 bits, which is above Certicom's 56 bit minimum of SEC 1. 58 bits was chosen because it can be partitioned into aesthetically pleasing groups of 5.

// From ecctest6


// Crypto++ Includes

//   Expedient Implementation of a Near NULL Hash

#include "cryptlib.h"

#include "iterhash.h"


// TRUEHash

// A hash that always returns 0x01

// This is a Visual C++ workaround (possibly others)

// due to not being able to create a NULL HMAC class

// The NULL HMAC cannot compile due to a digest size of 0

// because of array sizing of 0 (major problems in SecByteBlock())

class TRUEHash : public CryptoPP::IteratedHashWithStaticTransform<
    CryptoPP::word32, CryptoPP::BigEndian, 32, 4, TRUEHash> 
{
    public:
    static void InitState(HashWordType *state)
    {
        state[0] = 0x01; return; 
    }
    static void Transform(CryptoPP::word32 *digest,
        const CryptoPP::word32 *data) 
    { 
        return; 
    }
    static const char *StaticAlgorithmName()
    {
        return "TRUE HASH";
    }
};

With the shim class in place, a new specialized ECIESNullT class< > was created. Notice the introduction of TRUEHash to DL_EncryptionAlgorithm_Xor< >.

// Crypto++ Includes

//   Template Specialization modification of

//   struct ECIES in ecccrypto.h

#include "pubkey.h"

#include "dh.h"

#include "sha.h"

#include "eccrypto.h"

#include "ecp.h"


template <class EC, 
    class COFACTOR_OPTION = CryptoPP::NoCofactorMultiplication,
    bool DHAES_MODE = false>
struct ECIESNullT
    : public CryptoPP::DL_ES<
    CryptoPP::DL_Keys_EC<EC>,
    CryptoPP::DL_KeyAgreementAlgorithm_DH<typename EC::Point, COFACTOR_OPTION>,
    CryptoPP::DL_KeyDerivationAlgorithm_P1363<typename EC::Point,
    DHAES_MODE, CryptoPP::P1363_KDF2<CryptoPP::SHA1> >,
    CryptoPP::DL_EncryptionAlgorithm_Xor<
    CryptoPP::HMAC<TRUEHash>, DHAES_MODE>,
    CryptoPP::ECIES<EC> >
{
    static std::string StaticAlgorithmName()
    {
        return "ECIES with NULL T";
    }
};

Running ecctest6 produces the following output:

And the corresponding results with a false key:

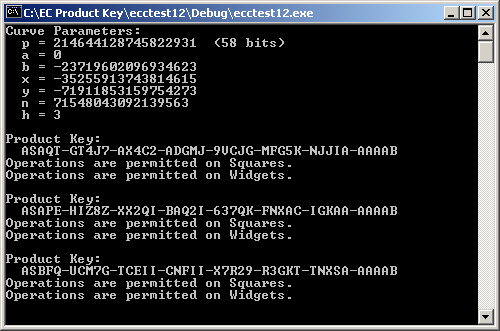
Bulk product key generation

ecctest7 exercises the ability to generate multiple cipher text Objects based on common curve parameters. Recall that ECIES parameters are the sextuple (p, a, b, Point G, n, h), where Point G is simply (x, y). This sample serves as proof of concept for the Key Generator and Key Validator.

KeyGen, as with ecctest7, exercises ECIES's property that a new, temporary key V is generated for each message M, producing a unique cipher text object (C,V,T) for each encryption operation. Note that the Decryptor has been dropped. It will exist in the validating software.

The perceptive reader should notice ECIES cipher text redundancy. The reader can further reduce the size of the generated Product Key by removing the redundant bytes after Base32 encoding before PrettyPrint.; and prepending and/or appending before the Base32 decoding, saving an additional 7 bytes of Base32 encoding. As a concrete example, a 56 bit curve produces a 31 byte key. 31 - 7 = 24, which groups aesthetically into six groups of four (xxxx-xxxx-xxxx-xxxx-xxxx-xxxx). Note that the additional bytes are required for decoding, but do not necessarily need to be keyed by the user.

The following is the Product Key generating program.

// From KeyGen (Key Generator)


// The Features Available...

const unsigned int FEATURE_EVALUATION  = 0x01;  // 0000 0001

const unsigned int FEATURE_USE_SQUARES = 0x02;  // 0000 0010

const unsigned int FEATURE_USE_CIRCLES = 0x04;  // 0000 0100

const unsigned int FEATURE_USE_WIDGETS = 0x08;  // 0000 1000

const unsigned int FEATURE_MAGIC = 0xAAAA << 16;
const unsigned int FEATURE_MAGIC_MASK = 0xFFFF << 16;

// Crypto++ Includes

// Expedient Implementation of a Near NULL Hash

#include "cryptlib.h"

#include "iterhash.h"


// TRUEHash

// A hash that always returns 0x01

class TRUEHash : public CryptoPP::IteratedHashWithStaticTransform<
    CryptoPP::word32, CryptoPP::BigEndian, 32, 4, TRUEHash> 
{
    public:
    static void InitState(HashWordType *state)
    { 
        state[0] = 0x01; return; 
    }
    static void Transform(CryptoPP::word32 *digest,
        const CryptoPP::word32 *data) { return; }
    static const char *StaticAlgorithmName()
    {
        return "TRUE HASH";
    }
};

// Crypto++ Includes

// Template Specialization modification of

// struct ECIES in ecccrypto.h

#include "pubkey.h"

#include "dh.h"

#include "sha.h"

#include "eccrypto.h"

#include "ecp.h"


template <class EC, 
    class COFACTOR_OPTION = CryptoPP::NoCofactorMultiplication,
    bool DHAES_MODE = false>struct ECIESNullT
    : public CryptoPP::DL_ES<
        CryptoPP::DL_Keys_EC<EC>,
        CryptoPP::DL_KeyAgreementAlgorithm_DH<typename EC::Point,
        COFACTOR_OPTION>,
        CryptoPP::DL_KeyDerivationAlgorithm_P1363<typename EC::Point,
        DHAES_MODE, CryptoPP::P1363_KDF2<CryptoPP::SHA1> >,
        CryptoPP::DL_EncryptionAlgorithm_Xor<CryptoPP::HMAC<TRUEHash>,
        DHAES_MODE>,
        CryptoPP::ECIES<EC> >
{
    static std::string StaticAlgorithmName()
    {
        return "ECIES with NULL T";
    }
};

// Crypto++ Includes

//   Required for main(...)

#include "cryptlib.h"

#include "osrng.h"      // Random Number Generator

#include "eccrypto.h"   // Elliptic Curve

#include "ecp.h"        // F(p) EC

#include "integer.h"    // Integer Operations

#include "base32.h"     // Encodeing-Decoding

#include "nbtheory.h"   // ModularSquareRoot(...)


int main(int argc, char* argv[]) 
{
    byte* CipherText = NULL;
    byte* EncodedText = NULL;
    CryptoPP::AutoSeededRandomPool rng;

    try 
    {
        // PlainText (Message M)

        unsigned int Features = 0;
        Features |= FEATURE_MAGIC;
        Features |= FEATURE_USE_WIDGETS;
        Features |= FEATURE_USE_SQUARES;

        // Runtime Sizes...

        unsigned int PlainTextLength = sizeof( Features );
 
        // User Defined Domain Parameters

        CryptoPP::Integer p("214644128745822931");
        CryptoPP::Integer a("0");
        CryptoPP::Integer b("-23719602096934623");
        CryptoPP::Integer n("71548043092139563");   // R from ECB

        CryptoPP::Integer h("3");                  // S from ECB, must be <= 4

        CryptoPP::Integer x("-35255913743814615");
        CryptoPP::Integer y("-71911853159754273");

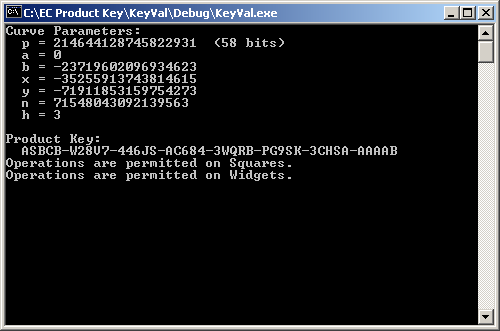
        PrintCurveParameters( p, a, b, x, y, n, h ); std::cout << std::endl;

        CryptoPP::ECP ec( p, a, b );
        ECIESNullT< CryptoPP::ECP >::PrivateKey    PrivateKey;
        ECIESNullT< CryptoPP::ECP >::PublicKey     PublicKey;

        // Curve Initialization

        PrivateKey.Initialize( ec, CryptoPP::ECP::Point( x, y ), n );
        PrivateKey.MakePublicKey( PublicKey );
        ECIESNullT< CryptoPP::ECP >::Encryptor Encryptor( PublicKey );

        // No Need for ECIESNullT< CryptoPP::ECP >::Decryptor

        // in the Key Generator. The decrypting software will employ it.

        const unsigned int ITERATIONS = 128;
        for(int i = 0; i < ITERATIONS; i++ ) 
        {
            unsigned int CipherTextLength = Encryptor.CiphertextLength( 
                PlainTextLength );
            if( 0 == CipherTextLength )
            { 
                throw std::string("plaintextLength is not valid (too long)"); 
            }

            // Scratch for Encryption

            CipherText = new byte[ CipherTextLength ];
            if( NULL == CipherText )
            { 
                throw std::string( "CipherText Allocation Failure" ); 
            }

            // Encryption

            Encryptor.Encrypt( rng, 
                reinterpret_cast<const byte*>( &Features ),
                PlainTextLength, CipherText);

            // Base 32 Encoding

            CryptoPP::Base32Encoder Encoder;
            Encoder.Put( CipherText, CipherTextLength );
            Encoder.MessageEnd();

            // Scratch for Base 32 Encoded cipher text

            unsigned int EncodedTextLength = Encoder.MaxRetrievable();
            EncodedText = new byte[ EncodedTextLength + 1 ];
            EncodedText[ EncodedTextLength ] = '\0';

            // Fetch Base 32 Encoded cipher text

            Encoder.Get( EncodedText, EncodedTextLength );

            // Pretty Print 

            const unsigned int BREAK = 5; 
            for(unsigned int i = 0; i < EncodedTextLength; i++)
            {
                if( 0 != i && 0 == i % BREAK )
                { 
                    std::cout << "-"; 
                }
                std::cout << EncodedText[ i ];
            }
            std::cout << std::endl;

            // Cleanup

            delete[] CipherText;
            delete[] EncodedText;
        }

        catch( CryptoPP::Exception& e ) 
        {
            std::cerr << "Crypto++ Error: " << e.what() << std::endl;
        }

        catch( std::string& s ) 
        {
            std::cerr << "Error: " << s << std::endl;
        }

        catch (...) 
        {
            std::cerr << "Unknown Error" << std::endl;
        }
        return 0;
    }
}

Product key validation

KeyVal is the driver program that validates Product Keys. The reader should choose a Product Key from this article and use it as a parameter to Decryptor.Decrypt(...) after removing the Base32 encoding.

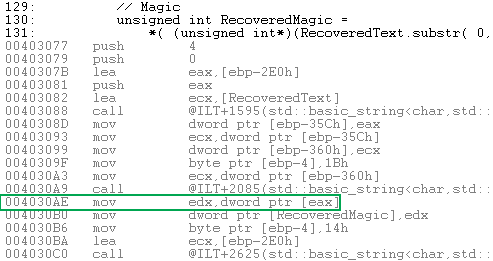
The reader should be aware of the side effects of casting a byte[] to an unsigned int*, as in excerpts from ecctest7 below. It is a C++ side-effect, not a Crypto++ effect.

// Conversion for Convenience

// Don't be fooled:

// RecoveredFeatures = static_cast<unsigned int>( *RecoveredText );

// only converts byte[ 0 ], not bytes[ 0 - 4 ]

// And you'll blame the mistake on Encryption\Decryption...

unsigned int RecoveredFeatures =
    *(reinterpret_cast<unsigned int*>( RecoveredText ) );

Screenshot - image027.gif

Screenshot - image028.gif

Securely saving key or activation state to the registry

Product Keys and Program Activation states can be securely saved to the Windows Registry. Please see An AES Encrypting Registry Class for a discussion and implementation.

Summary

Although this article does not present a concrete implementation of an Optimal Compact Product Key System, the groundwork for such a system has been outlined. By using ECIES as specified in IEEE 1363 and ANSI X9.63 and implemented in Crypto++, one can side-step most patent issues involved with Elliptic Curve Cryptography. However, there may be other implications in the application of ECC to the realm of Product Keys and Product Activations.

Acknowledgments

  • Wei Dai for Crypto++ and his invaluable help on the Crypto++ mailing list
  • Dr. A. Brooke Stephens who laid my Cryptographic foundations
  • Marcel Martin for his work on ECB to facilitate this Article and critiques of the Article's EC description correctness
  • Jason Smethers for his Elliptic Curve Sample, which served as an early basis for this article (see ecctest1)

Revisions

  • 06.01.2007 Article edited and moved to the main CodeProject.com. article base
  • 12.13.2006 Removed Setup Program Section
  • 12.13.2006 Removed User Interface Design Consideration Section
  • 12.11.2006 Updated Article Citation Links
  • 11.26.2006 Added reference to Product Activation Based on RSA Signatures
  • 11.26.2006 Added Generated Assembly Code of string::data() Cast
  • 11.21.2006 Added reference to Product Keys Based on the Advanced Encryption Standard (AES)
  • 11.18.2006 Uploaded DPVal (Domain Parameters Validation Program)
  • 11.18.2006 Added Certicom requirement of a, b, x, y be in the interval [0, p-1]
  • 11.16.2006 Updated Article Citation Links
  • 11.16.2006 Added Note on Downloads
  • 11.16.2006 Added Note on Reverse Engineering and Temporary Cipher Text Key
  • 11.14.2006 Original Release

Checksums

ecctest1.zip
MD5: E3F55FCA3B94C0BB9DD69805E14C1D8C
SHA-1: 5E367F3FBF68CC0CF623C1CC774B64BE4A77F00E
SHA-256: 6EAB74049D7832A03049AFBFD5F951CD7774DFC03F6826D0EF92C0AC4E7053DE

ecctest2.zip
MD5: 190EA42556D3896D118D58C156BD4E8F
SHA-1: 4CD210D92D534B267C21E30F40B48407BC7310FC
SHA-256: C2042E1994ED602164E944FC8B42A9C20231D14E4D49284D17D91A0F37606405

ecctest3.zip
MD5: 8A1A8CD7466E802DDEBE83564F16AA2A
SHA-1: D15C38A00E10C44545B33B430983DD3E3DB1AF17
SHA-256: C7691BF5F2E4D74938C0DCF073F551EB473166E6F70317890CCEE275178EF046

ecctest4.zip
MD5: 3EDE37CBCBACE34B5915439A7B14EFC8
SHA-1: 5F01BAAF9BE1A8B5756C751E8D454C31EA266228
SHA-256: A4E8A74668979A2D633B77AB8432BB156069224A303EE572534DF8C16E9BDEAF

ecctest5.zip
MD5: D7FB9BB017722AD616701CC8D8AB09F0
SHA-1: C83297CDFFD756B8367D7998A6981CA175A43A5D
SHA-256: 748B06AE1BFDEB2522AE3714AC2D3EC7F5067DD8DF5A75119EA4995E30D940F6

ecctest6.zip
MD5: 8B8C65D08D51DBD3B7C02CAD5F95ABEA
SHA-1: 22C92DB0B114F4BA7B3431E7FE0CCA178813970C
SHA-256: B60925480D6342FEAE2E70FE4EC1EAC052443925E0E74EFF5D84B4D9EF3149C6

ecctest7.zip
MD5: D6789D5492CD7AB663E3082202465C25
SHA-1: 13696CF1FC6FCE5EE0FEFDE147C35CFCA28D1A2B
SHA-256: 4F68DD905D1AF9608FE72C29A3D4771EE7C0F4B9858408817F60D3154226712D

ecctest1to7.zip
MD5: 531D016FA1FB684B24609C0DC89756B5
SHA-1: 692E343B98446BD8CE5031B80F1F8B25BEF06177
SHA-256: 3836CF6917939E4EEA27D2EEA995A03FB8E71203607B66A9085E997FAD48AFA5

ecc160test.zip
MD5: 35B64712131821F4755D8D435B91A5DD
SHA-1: CC999725B434B627983F0BE0DCA603B38086E528
SHA-256: 7F43C899734F0E389F9C7B1496576F2C8C1569390FEFE23D23F40F43DB37BB07

License

This article has no explicit license attached to it but may contain usage terms in the article text or the download files themselves. If in doubt please contact the author via the discussion board below.

A list of licenses authors might use can be found here



Permalink

Privacy
Cookies
Terms of Use
Layout: fixed | fluid

Article Copyright 2006 by Jeffrey Walton
Everything else Copyright © CodeProject, 1999-2024

Web01 2.8:2024-10-19:1