Introduction
As a follow up on my tip/trick on Converting Geographic Coordinates (here), I would like to discuss the more advanced topic of coordinate transformation. I have marked this tip/trick 'Advanced' because the subject is for an advanced user audience (the code is pretty easy). If you are familiar with coordinate conversions, transformations and datum shifts, this tip is for you. If not, you can read about it in: Coordinate systems, projections and datum transformations and more in depth Coordinate transformations.
Background
I have been a GIS user for a long time and have always been interested in coordinate conversion and the code behind it. A long time ago, I even started my own 'projection library in VBA', which died a silent death. Fortunately, there are some really good and really free programs and DLLs available on the subject. I'm a great fan of the free GIS package QGIS (just my opinion). QGIS and many other applications make use of C++ lib called proj.4 which has been around for some time now and is tried and tested, refer to OSGeo Proj.4. As far as I know, two ports to .NET are available: Proj4Net and the Dotspatial.Projections DLL part of the DotSpatial project. I started out with Proj4Net, because it is a small, dedicated DLL, but stopped after finding out that it only supported a few standard projections. For example, if you want to convert coordinates from the Dutch national grid (called RDnew) to something else, you need to handle the Oblique Stereographic projection, which Proj4Net does not. Then, I turned to DotSpatial.Projections and got it all working. The DLL is 19MB big, but worth it; it's compiled for .NET4.0. There's a wealth of methods in this DLL and as well as documentation on the web, so I will not cover all the functionality provided. I will just show its use in .NET and benchmark it against a coordinate conversion package developed by the Hydrographic Service of the Royal Netherlands Navy called PCTrans which has proven to me to be very accurate; it is free and you can download it here (but it is really useful in the Dutch On,- and Offshore and you'll have to leave your email address).
One last word of warning: any coordinate conversion or transformation is an approximation. There's no such thing as an exact conversion. All comes down to the error in the conversion being good (small) enough for the goals you have. If you want to be exact, measure your coordinates with the best GPS you can get or buy and do not convert them.
The Test...
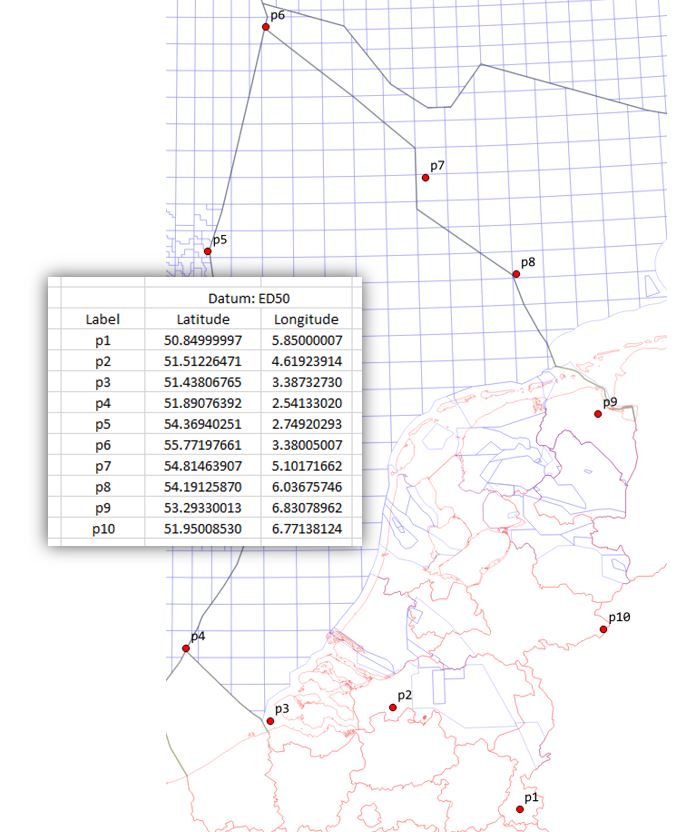
I will show a test on 10 points with source coordinates of latitudes and longitudes on datum ED50 in decimal degrees and convert them to eastings and northings (X and Y's) of the RDnew projection used onshore Holland. The ED50 datum uses the International Ellipsoid of 1924 (eq. to "Hayford-Ellipsoid" of 1909). The RDnew projection is an Oblique Stereographic projection on the Bessel Ellipsoid of 1841. The above conversion implies a datum shift from the Int1924 ellipsoid to the Bessel1841 ellipsoid. The validity of the RDnew projection is only the land part of The Netherlands (where also an error correction grid is available) but I will apply it to the offshore as well just for testing. The map below shows the test data.
To reference the DotSpatial.Projections library, I use the package manager of SharpDevelop. You can also get it through the NuGet gallery. Below is a picture of the package manager.

Coding the program is a peace of cake (C# code is found more below):
Module Program
Sub Main()
Console.WriteLine("VB.NET: Test coordinate conversion from ED50 to RD New")
Dim x As Double() = {5.85000007,4.61923914,3.38732730,2.54133020,2.74920293, _
3.38005007,5.10171662,6.03675746,6.83078962,6.77138124}
Dim y As Double() = {50.84999997,51.51226471,51.43806765,51.89076392,54.36940251, _
55.77197661,54.81463907,54.19125870,53.29330013,51.95008530}
Dim z(x.Length-1) As Double
For i As Integer = 0 To z.Length-1
Console.WriteLine("input geographic ED50 p{0} = {1} {2}",i+1,x(i),y(i))
Next
Dim xy(2*x.Length) As Double
Dim ixy As Integer = 0
For i As Integer = 0 To x.Length-1
xy(ixy) = x(i)
xy(ixy+1) = y(i)
z(i) = 0
ixy += 2
Next
Dim proj4_ed50 As String = "+proj=longlat +ellps=intl +towgs84=-87,-98,-121,0,0,0,0 +no_defs"
Dim proj4_rdnew As String = "+proj=sterea " & _
"+lat_0=52.15616055555555 +lon_0=5.38763888888889 +k=0.9999079 +x_0=155000 +y_0=463000 " & _
"+ellps=bessel +towgs84=565.417,50.3319,465.552,-0.398957,0.343988,-1.8774,4.0725 " & _
"+units=m +no_defs"
Dim src As DotSpatial.Projections.ProjectionInfo = _
DotSpatial.Projections.ProjectionInfo.FromProj4String(proj4_ed50)
Dim trg As DotSpatial.Projections.ProjectionInfo = _
DotSpatial.Projections.ProjectionInfo.FromProj4String(proj4_rdnew)
DotSpatial.Projections.Reproject.ReprojectPoints(xy,z,src,trg,0,x.Length)
ixy = 0
For i As Integer = 0 To x.Length-1
Console.WriteLine("output RD New {0} = {1} {2}",i+1,xy(ixy),xy(ixy+1))
ixy += 2
Next
Console.Write("Press any key to continue . . . ")
Console.ReadKey(True)
End Sub
End Module
First, the LatLons are loaded into separate arrays. Then, I show how to rewrite the individual arrays into arrays that can be passed to Proj4 which uses a sort of interlaced x and y array {x1,y1,x2,y2....} and a separate array of z values (which I set to 0).
Setting up a projection is easy by declaring a ProjectionInfo class and defining the source and target projections by a string. Proj4 allows you to define a projection in 4 different ways: FromAuthorityCode, FromEpsgCode, FromEsriString and FromProj4String. For a description of these methods, look here. I prefer the Proj4 string because it is concise, readable and moreover, allows you to tweak the projection parameters or even define your own custom projection easily. The main point here is the +towgs84 part of the string which defines the datum shift. The parameters following this flag define how the current datum can be transformed to reference WGS84 ellipsoid (= "to WGS84"). Having defined this, allows coordinates to be converted to different projections. Proj4 handles a 3 parameter transformation (translation only) and a 7 parameter (translation + rotation + scaling) transformation. The exact definition of these 3 or 7 numbers is not trivial and depending on method (Helmert, Bursa-Wolf, Molodensky, etc.) and sense of rotation. There is a lot of background information on the web which parameters are best for which area; just do a search on "proj4 3 or 7 parameters transformation". It is not difficult to make a small typo or use wrong parameters and end up with coordinates a million miles from where you thought they would be... Best practice is to use a test point or set of which you are sure the transformed coordinates are correct and compare them to your results. In my case, I have taken the Proj4 (including the towgs84 parameters) strings from QGIS where they are logged whenever you change the coordinate reference system. My test set to check on the validity is the one presented here. From the code, it can be seen that I use a 'simple' 3 parameter transformation from datum ED50 to WGS84 and a 7 parameter transformation from Bessel1841 to WGS84.
DotSpatial.Projections.Reproject.ReprojectPoints(xy,z,src,trg,0,x.Length) does the actual conversion, where xy and z are the coordinate arrays, src and trg are the from- and to projections and 0 and x.Length are the start index and length of the array. The converted coordinates are written to the input arrays (or ByRef arguments in VB.NET speak).
The C# code is here:
using System;
namespace CPdemoInCSharp
{
class Program
{
public static void Main(string[] args)
{
Console.WriteLine("C#: Test coordinate conversion from ED50 to RD New");
double[] x = {5.85000007,4.61923914,3.3873273,2.5413302,
2.74920293,3.38005007,5.10171662,6.03675746,6.83078962,6.77138124};
double[] y = {50.84999997,51.51226471,51.43806765,
51.89076392,54.36940251,55.77197661,54.81463907,54.1912587,53.29330013,51.9500853};
double[] z = new double[x.Length];
for (int i = 0; i <= z.Length - 1; i++) {
Console.WriteLine("input geographic ED50 p{0} = {1} {2}", i+1, x[i], y[i]);
}
double[] xy = new double[2 * x.Length];
int ixy = 0;
for (int i = 0; i <= x.Length - 1; i++) {
xy[ixy] = x[i];
xy[ixy + 1] = y[i];
z[i] = 0;
ixy += 2;
}
string proj4_ed50 = "+proj=longlat
+ellps=intl +towgs84=-87,-98,-121,0,0,0,0 +no_defs";
string proj4_rdnew = "+proj=sterea +lat_0=52.15616055555555
+lon_0=5.38763888888889 +k=0.9999079 +x_0=155000 +y_0=463000 +ellps=bessel
+towgs84=565.417,50.3319,465.552,-0.398957,0.343988,-1.8774,4.0725 +units=m +no_defs";
DotSpatial.Projections.ProjectionInfo src =
DotSpatial.Projections.ProjectionInfo.FromProj4String(proj4_ed50);
DotSpatial.Projections.ProjectionInfo trg =
DotSpatial.Projections.ProjectionInfo.FromProj4String(proj4_rdnew);
DotSpatial.Projections.Reproject.ReprojectPoints(xy, z, src, trg, 0, x.Length);
ixy = 0;
for (int i = 0; i <= x.Length - 1; i++) {
Console.WriteLine("output RD New p{0} = {1} {2}", i+1, xy[ixy], xy[ixy + 1]);
ixy += 2;
}
Console.Write("Press any key to continue . . . ");
Console.ReadKey(true);
}
}
}
The Result...
The result and comparison of the conversion are listed in the below table and also attached as a spreadsheet to this tip.

As can be seen, the results compared to the output of PCTrans are very close. When PCTrans converts coordinates to RDnew, it warns if the input coordinates are outside the area of assured validity and correction grid availability. Where the input coordinates are with the valid area, the absolute differences are no more than 18cm max. Note that in this valid area, PCTrans applies an extra correction. Outside the valid area (and where PCTrans does not apply any corrections) differences are below 1cm. For my work, this accuracy is good enough. If you need accuracy at mm scale, these results may not impress you; however keep in mind that conversion is an approximation to begin with and is never 100% accurate.
I hope you'll find this tip useful...
History
- 18th January, 2016: Initial draft
