Introduction
In brushing up on 3-D Graphics programming, I considered some of my options:
- C++ and DirectX
- C# and managed DirectX
- WPF
- C# and OpenGl
(Here is a good list of other options.) I decided against the C++ and DirectX option because I prefer C# to C++. Managed DirectX is no longer supported by Microsoft, so I also decided against that option. I initially worked with WPF and found it a bit too challenging to use XAML and C#, so I decided on the C# and OpenGl option. This project uses the Tao OpenGl framework. The key to using the Tao OpenGl framework is passing a handle (a pointer in C and C++ terminology) to a device context.
handleDvcCtx = (uint)pnlViewPort.Handle;
OpenGLControl.OpenGLInit(ref handleDvcCtx, pnlViewPort.Width, pnlViewPort.Height, ref error);
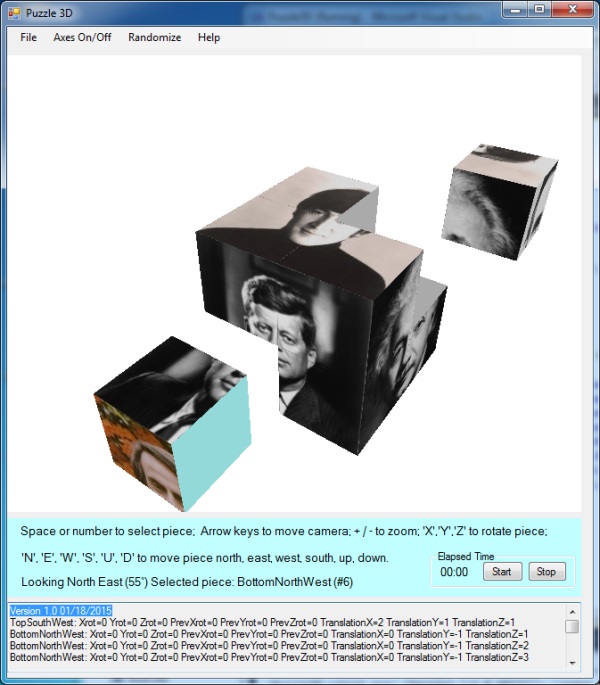
My objective was to build a rudimentary "game" where some number of game pieces, perhaps LEGO® or Tetris type blocks, could be manipulated in the 3-D world by the player. She should be able to move and rotate them independently, and move the camera to view them. For this project, all rotations are 90 degrees about the cube's local axes (although I would appreciate suggestions for how to rotate about the world axes as well as the local axes). I decided to make a 3-D puzzle consisting of 8 cubes illustrated in the screenshot above. (The cubes - the game pieces - can be manipulated with keystrokes described below).
Rotations and translations in 3-D programming involve matrix manipulation, including matrix multiplication which is, in general, not commutative. I provided a Matrix class which contains some matrix manipulation methods and a number of links on matrix arithmetic. OpenGl uses the concept of the matrix stack which is used in this code. For newer versions of OpenGl, there are alternatives to the matrix stack which this project does not currently use.
In order to draw a cube with textures, I modified the GLUT cube by converting it from C++ to a C# class called Cube and added calls to glTexCoord2f. I also used the Game Programming Wiki's LoadTexture() method to load the images from files. Here is how to create a cube using the Cube class. See also Create() in GamePiece.cs (the image files must be in the bin\Debug or bin\Release directory):
Cube cube = new Cube(new string[]
{ "face_1c.bmp", "face_1e.bmp", "face_1a.bmp",
"face_1f.bmp", "face_1d.bmp", "face_1b.bmp" });
This project is compiled with the Visual Studio 2010 "Allow unsafe code" option as a pointer has to be passed to glVertex3fv using the fixed keyword:
fixed (float* face0 = &verts[faces[ndx, 0], 0])
{
float s = tex[(4 * ndx), 0];
float t = tex[(4 * ndx), 1];
Gl.glTexCoord2f(s, t);
Gl.glVertex3fv(face0);
}
Another place a pointer is used is in the call to SwapBuffers for which you will need the System.Runtime.InteropServices namespace.
In order to keep the size of the project small, I placed the images I used in a separate, optional downloadable file. The program uses the images shown in the screenshot above by default, but you can also specify your own images in the app.config file. I have included a sample app.config to show how to accomplish this. Place the images (.bmp or .png) in the project's Images directory. A post-build step copies them to \bin\Debug and \bin\Release. If you specify an image file that does not exist, a warning message is printed in the Visual Studio Output Window.
After you download and build the program, you can select "Help" from the menu bar to show the keystrokes used to manipulate the game pieces. Once you learn the keystrokes, with a little practice you can quickly move and rotate the game's puzzle pieces to where you want them. The puzzle is shown initially assembled. "Randomize" from the menu bar will randomly move and rotate the pieces. There is also an elapsed time clock you can start to see how long it takes you to solve the puzzle.
When the 'X', 'Y', or 'Z' keys are pressed to rotate the cube about the cube's local x, y, and z axes, it is necessary to keep track of the order of rotations since, as mentioned previously, matrix multiplications, and therefore, rotations, are not commutative. The strategy I chose was to have a class GamePiece, representing each game piece (which are essentially Cube's), and a class GameUniverse in which I build a list of game pieces. Each GamePiece has a current rotation matrix private float[] currentRotMatrix that is initialized to the identity matrix.
Then as the 'X', 'Y', or 'Z' keys are pressed to rotate the game piece, a temporary rotation matrix, rotMatrix is constructed and the currentRotMatrix is them multiplied by it. The current model view matrix is then multiplied by the currentRotMatrix. Even though each rotation is 90 degrees, I actually implemented a simple animation by performing nine individual 10 degree rotations, so that the cube is seen smoothly rotating rather than an instantaneous movement. The pause used is AnimationPauseMS and can be modified based on the speed of your machine. (I'm using a rather modest dual core processor machine and was quite pleased with the animation.)
Likewise, the translations are maintained in a matrix called currentTranMatrix. In ApplyTransformations(). You can see that the current model view matrix is multiplied by the translation matrix, followed by a multiplication by the currentRotMatrix. You might want to experiment with reversing the order of multiplications to prove to yourself that matrix multiplication is not commutative. For translations of the game pieces, the 'S' (for South) key moves the piece in the positive X direction, 'N' (for North) is the negative X direction, 'U' (for Up) is the positive Y direction, 'D' (for Down) is the negative Y direction, 'W' (for West) is the positive Z direction, and 'E' (for East) is the negative Z direction.
The locations and rotation state of each piece, as well as the camera settings (that is, the "state"), are can be saved in the Applications settings on exit and restored on startup; see SaveValues() and RetrieveValues() for details. Alternatively, the state can be saved in a text file using "File" from the menu bar, and restored by reading the file in using "Open".
Enhancements
The enhancements to this simple program are varied and only limited by one's imagination. Here are a few I came up with off the top of my head:
- Using the mouse to select, rotate, and translate the game pieces
- The ability to group two or more pieces together as a unit for translating or rotating
- Keeping all the translations and rotations in a list so that an "undo" feature can be implemented
- A way to indicate to the player that she has successfully solved the puzzle
- A "level of difficulty" option (e.g., more cubes, misleading images, multiple solutions)
Conclusion
I am not an OpenGl expert and therefore there are likely areas of this code that are not as efficient as they could be. I also am trying to come up with a way to rotate the cubes about the world axes when pressing the X, Y, and Z keys. (This version currently rotates about the cube's local axes.) Comments from OpenGl gurus appreciated.
History
