Balanced Index of an Array

• Download BalancedIndex-noexe.zip - 1.9 MB
• Download BalancedIndex.zip - 1.9 MB

Introduction

This tip presents two methods to find the balanced index of an array in C#.

An array's balanced index is the index where the sum of the values of all the array positions preceding the index is equal to the sum of the values of all positions after the index in the array. E.g.

1,2,1,0,3 -- The balanced (zero based) index is 2. The left cumulative sum is 1 + 2 and the right cumulative sum is 0 + 3.

1,2,3,3 -- The balanced index is 2 again. The left cumulative sum is 1 + 2 and the right cumulative sum is just 3.

1,1,1,1,1,1,1 - The balanced index is 3. The left cumulative sum is 1 + 1 + 1, and the right cumulative sum is 1 + 1 + 1.

One method with algorithmic complexity O(0.75n), meaning it must traverse the array on average 3 quaters of the way through, is much slower because it uses the reference type CummulativeSumPair to store the left and right cumulative sums. The other C# method has an O-value of O(1.5n) meaning it must traverse the array on average at least 1.5 times, uses value types to store the left sum and right sum, (and more importantly, it does not do any inserting into the middle of a list)  and therefore is much less memory and thereby also less processor intensive.

 public class CummulativeSumPair
{
 public int LeftCummulativeSum { get; set; }
 public int RightCummulativeSum { get; set; }
}

Background

The two methods can be compared via big O complexity analysis. One is 0(0.75n) the other O(1.5n). But because of memory usage, boxing and unboxing, and imprudent insertions into the middle of a list, the method with the higher O value (which should therefore be slower), is instead over 1000 times faster (depending on the value of n (the array length)).

Different solutions can be found by Googling for "balanced index of an array".

The gist of this tip is to present a couple ways to find the balanced index of an array in C#, and also show that in a managed language like C#, the usage of reference types, and insertion into a list,  and the boxing and unboxing thereby implied has a huge performance impact when compared to using algorithms with only value types. In this context, the algorithmic complexity might be less an indication of performance.

This tip has two methods to find the balanced index of an array, but the one with the higher algorithmic complexity (which should therefore be slower) is actually many times faster, because it uses value types (instead of reference types) -- and more so, because in the methode with the lower O vlaue i insert the reference type CummulativeSumPair into the middle of the list<CummulativeSumPair> causing a lot of memory movement.

A refactoring TODO (for myself or anyone using this tip) is to split this list into two lists and build the lists using only List.Add while at the same time keeping the methods low O-value, and then see by how much performance improves

Using the Code

The two methods to find the balanced index of an array are shown below.

As indicated above, the second one...

GetBalancedIndex_O1point5N(int[] inputArray)

...is about 133 times faster (for n=100 000), and 1000 times faster (for n=1000 000), even though its O-value is higher (and all else equal, should therefore be slower) than the second method.

GetBalancedIndex(int[] inputArray)

This is because GetBalancedIndex_O1point5N uses mostly value types like int (Int32)  and does not imprudently insert into the middle of a list. The second method GetBalancedIndex is reference type heavy, with a lot of boxing and unboxing because it inserts into the middle of a list<CummulativeSumPair>, making it very slow, even though it is algorithmically, with O-value O(0.75n), it should be faster.

        //This method has O(0.75n) but is slow
        public int GetBalancedIndex(int[] inputArray)
        {
            int leftSum = 0;
            int rightSum = 0;

            ListOfCumulativeSums = new List<CummulativeSumPair>();
            ListOfCumulativeSums.Capacity = inputArray.Count();
           
            //We move through the Array and there are no subloops the O-value can max be O(n)
            for (int i = 0; i < inputArray.Count() - 1; i++)
            {
                int endIndex = inputArray.Count() - 1 - i;

                rightSum += inputArray[endIndex];
                leftSum += inputArray[i];

                CummulativeSumPair leftCumulativeSum; 
                CummulativeSumPair rightCumulativeSum;

                //Here we are loading the ENTIRE List<cummulativesumpair> ListOfCumulativeSums
                //with Cummulativesumpair objects at each node.
                //We start at bothe ends of the list ListOfCumulativeSums,
                //and work our way to the middle of the list.
                //When i > endIndex we know the list is fully loaded
                if (i <= endIndex)
                {
                    leftCumulativeSum = new CummulativeSumPair();
                    rightCumulativeSum = new CummulativeSumPair();

                    //When we start we just add two CummulativeSumPair objects to the list
                    //The first one is the first object in the list
                    //The second one will be the last node.
                    if (ListOfCumulativeSums.Count() == 0)
                    {
                        ListOfCumulativeSums.Add(leftCumulativeSum);
                        ListOfCumulativeSums.Add(rightCumulativeSum);
                    }
                    else
                    {
                        //If the array has a dead center mittle (inputArray.Count() is an Odd number)
                        //We just insert one CummulativePairSum object
                        if (i == endIndex)
                        {
                            ListOfCumulativeSums.Insert(i, leftCumulativeSum);
                            rightCumulativeSum = leftCumulativeSum;
                        }
                        //Otherwise we go to the center of the list and insert at index's i and i+1.
                        //This is performancewise very costly, since it causes the entire 2nd half of the
                        //array to move in memory, unboxed and then boxed, for each item in the 2nd half
                        //of the array with index i and above.
                        //As if this is not costly enough, the insert in the middle is done twice.
                        else
                        {
                            ListOfCumulativeSums.Insert(i, leftCumulativeSum);
                            ListOfCumulativeSums.Insert(i+1, rightCumulativeSum);
//TODO, refactor:
//Split ListOfCumulativeSums into two lists so the above performance costly inserts into 
//the middle of the list can be avoided.
//Then compare again with the performancce of the
//GetBalancedIndex_O1point5N method
                        }
                    }
                 }
                //When i > endIndex we know the list, ListOfCumulativeSums, is fully loaded
                //So instead of creating a new CummulativeSumPair we just get them from the list,
                //as we see below in the else clause
                else
                {
                    leftCumulativeSum = ListOfCumulativeSums[i];
                    rightCumulativeSum = ListOfCumulativeSums[endIndex];
                }

                //The subtlety here is that when index i is in the left part of the array 
                //(less than count()/2)
                //and endIndex is the right side of the array, then leftCumulativeSum is inded 
                //from the left side,
                //and  rightCumulativeSum is indeed from the right side.

                // But when index i is in right half of the array,
                //and index endIndex is in the left side of the array, 
                //then leftCumulativeSum is actually retrieved from the right side. 
                //This CummulativePair sum object was already
                //inserted in a previous iteration as a rightCumulativeSum CumulativeSumPair object 
                //and had
                //already its RightCummulativeSum int property already set.
                //With i on the right side of the array this same CummulativeSumPair object (which we
                //call now "leftCumulativeSum" it is just the reference name to wherever i is
                //pointing in the array) it now will
                //also have its LeftCummulativeSum int property set.
                //The same explanation apples to the "rightCumulative" sum.  It is just a reference
                //to CummulativeSumPair that endIndex is pointing too.
                leftCumulativeSum.LeftCummulativeSum = leftSum;
                rightCumulativeSum.RightCummulativeSum = rightSum;

                //when i is in the middle or has traversed to the right side, then
                //we have summed up from both ends to the middle.
                //It makes sence then to ask for the objects that index i and endIndex are
                //pointing to, on whether their LeftCummulativeSum == RightCummulativeSum
                //On average it is when we get to the middle of the second half of the array
                //that a balanced index can be found. Therefore the estimate O(0.75n)
                if (i >= endIndex)
                {
                    if (leftCumulativeSum.LeftCummulativeSum == leftCumulativeSum.RightCummulativeSum)
                    {
                        return i;
                    }
                    else if (rightCumulativeSum.LeftCummulativeSum == 
                    rightCumulativeSum.RightCummulativeSum)
                    {
                        return endIndex;
                    }
                }
            }

            return -1;
        }

        //This method has O(1.5n) a higher O value than the above method, but it is faster
        public int GetBalancedIndex_O1point5N(int[] inputArray)
        {
            int i = 0;
            int totalArraySum = 0;

            int leftsum = 0;

            for (i = 0; i < inputArray.Count(); i++)
                totalArraySum += inputArray[i];

            for (i = 0; i < inputArray.Count(); i++)
            {
                totalArraySum -= inputArray[i];

                if (i > 0  && leftsum == totalArraySum)
                    return i;

                if (i == inputArray.Count() - 1 )
                {
                    return -1;
                }

                leftsum += inputArray[i];
            }

            return -1;        
        }

Points of Interest

There is a test project in the solution included with this tip. The test cases it includes should be self documenting with comments.

The time duration tests in the test project call the GetVeryLongInArray(int) method.

It is simple to increase the input (the same value at both places in the code that it is called) and then (re)run the tests with Visual Studio. And compare the time it takes to verify what this tip is claiming.

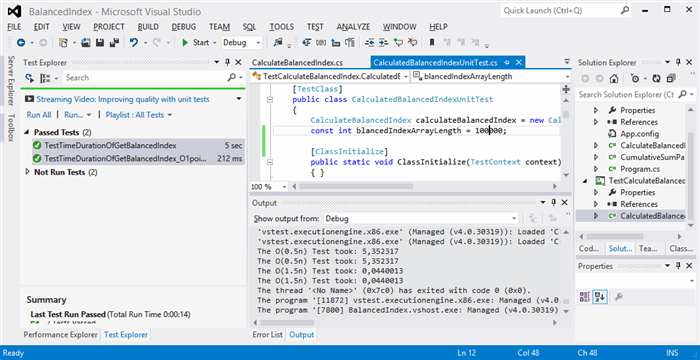
Because this article is getting some attention, I am updating here. I added the balancedIndexArrayLength const variable to the test project.

In the picture below, I show that I then run the tests TestTimeDurationOfGetBalancedIndex and TestTimeDurationOfGetBalancedIndex_O1point5N. In the output window, you can see that with balancedIndexArrayLength = 100 000, the O(1.5n) test method TestTimeDurationOfGetBalancedIndex_O1point5N is about 5,35/0.04 = 133 times faster than the O(0.75n) test method TestTimeDurationOfGetBalancedIndex.

What would happen, if I increased balancedIndexArrayLength to 1000 000 (10 times as much as before)?

I did it, and the time values I got from the two test methods were:

594.5 seconds for the O(0.75n) TestTimeDurationOfGetBalancedIndex method.

0.5 seconds for the O(1.5n) TestTimeDurationOfGetBalancedIndex_O1point5N method.

Meaning the O(1.5n) method was this time 1099 times faster.

I updated the solution and test project (I am using Visual Studio 2013) so you can try it yourselves.

History

This post contains some repetition as its first version was rejected as unclear and incomplete. I hope it is now clear and complete.