Introduction
We know that a method is a named block of executable instructions callable from many places in our program. In general, there are two types of them: Iterative and Recursive.
Iterative methods have loop constructs in their body and are frequently used by programmers. Recursive ones, on the other hand, are more complex and using them takes more work.
In this article, we’ll be introduced to background concepts behind Recursion through basic number theory. So, if you’re ready to see the Java-Math friendly relationship, go ahead!
Background
Recursion is a technique that leads to elegant solutions to problems that are difficult to program using simple loops.
It means using recursive approaches in appropriate situations is highly recommended so you should be familiar with these techniques to level up your experience in Java programming.
Prerequisites
Java
Recursion
Besides calling other methods, a method can also call itself. This is called Recursion. If you ask me “Why recursion works in Java?”, I would tell you because it works in Mathematics. In fact, recursion is related to a famous subject in math called Induction.
In the following part, I’ll cover mathematics behind the idea. For now, the definition of recursion is enough for us. More details are demonstrated in examples.
Mathematics
Mathematical Induction
Mathematical induction is a method of mathematical proof typically used to establish a given statement for all natural numbers. It is a form of direct proof, and it is done in two steps.
Simply put, it says if a proposition P is true for 1 and if we can conclude that if n satisfies P, then n+1 also satisfies P; then all of the natural numbers satisfy P. See https://en.wikipedia.org/wiki/Mathematical_induction .
Natural Numbers
A natural number is a positive whole number. The set of all natural numbers is denoted By N. So 1, 2, 545 are natural numbers but 0, -6 and 12.5 are not. See https://en.wikipedia.org/wiki/Natural_number.
Integers
An integer is either a natural number or 0 or negative of a natural number. The set of all integers is denoted by I (or sometimes Z, in German ‘zahlen’ means number). So 1, -9 and 0 are integers but 0.5 , -6.7 and Pi are not. See https://en.wikipedia.org/wiki/Integer.
Division Algorithm
Let m and n be two arbitary integers. We say m divides n or n is a multiple of n if there exists an integer q such as n = m*q . In this case q is called quotient, m is divisor and n is dividend. There is a fundamental theorem called Division Algorithm which says for arbitary positive integers m and n, m not equal to 0, there exist unique pair of integers, namely r and s, such that n = m*q + r with r<m and greater than or equal to 0. In the previous equation r is called remainder. So if m divides n then r must be 0 in division algorithm. See https://en.wikipedia.org/wiki/Division_algorithm
G.C.D.: Greatest Common Divisor
Let m and n be two integers, both not 0 at the same time. We say d is a common divisor of m and n if d divides both of them. It's easy to show that there exists a maximum divisor for our m and n which is called Greatest Common Devisor ( G.C.D. ).
We use gcd(m,n) to denote the G.C.D of m and n. It has many properties but one of them is used here which says if m is greater than or equal to n, then gcd(m,n) = gcd(m-n,n). See https://en.wikipedia.org/wiki/Greatest_common_divisor.
Factorial Function
Let n be a natural number. 1*2*3*...*n-2*n-1*n is denoted by n! and read " n factorial ". So factorials are just multiplications although they play very important roles in number theory specially combinatorics. We need this important equality : n! = n * ( n-1 )! . See https://en.wikipedia.org/wiki/Factorial .
Fibonacci Sequence
A sequnce is simply a string of numbers. For example 1, 2, 3, ... is the sequnce of natural numbers. Each term in a sequence is determined by a numerical value called index. So 2 in our example sequence has the index of 2 because it's the second term of the sequence.
Fibonacci sequence is a special sequence in the following manner : 1, 1, 2, 3, 5, 8, 13, ...
It has many interesting properties. One of them is its declaration which is recursively in this manner : nth term of the sequence is the sum of two preceding terms. See https://en.wikipedia.org/wiki/Fibonacci_number .
Using the Code
Now we’re ready to tackle the Recursion. In order to demonstrate concepts, we develop a class named Recursion for calculating multiplication, factorial, Fibonacci, GCD and some other. The Recursion class has both Iterative and Recursive methods so we can compare them easily.
Theory is enough. Let’s get coding.
package Main;
* @author MrSH http:www.thevelop.ir
*/
public class Recursion {
public static long iterativeMultiplication(long x, long y){
long production = 0;
for (int i = 0; i < y; i++)
production+=x;
return production;
}
public static long recursiveMultiplication(long x, long y){
if(y == 1)
return x;
return x + recursiveMultiplication(x, y-1);
}
public static long iterativeFactorial(long n){
long factorial = 1;
for (int i = 1; i <= n ; i++) {
factorial *= i;
}
return factorial;
}
public static long recursiveFactorial(long n){
if (n==1 || n== 0)
return n;
return n * recursiveFactorial(n-1);
}
public static long iterativeFibonacci(long n){
long x=1, y=1, z=1;
for (int i = 3; i <= n; i++) {
z=x+y;
x=y;
y=z;
}
return z;
}
public static long recursiveFibonacci(long n){
if (n==1 || n==2)
return 1;
return recursiveFibonacci(n-1)+recursiveFibonacci(n-2);
}
public static long iterativeGCD(long x, long y){
long GCD = 1;
long minimum = Math.min(x, y);
for (int i = 1; i <= minimum; i++) {
if (x%i == 0 && y%i == 0) {
GCD = i;
}
}
return GCD;
}
public static long recursiveGCD(long x, long y){
if(x==1 || y == 1)
return 1;
if (x==0)
return y;
if(y==0)
return x;
if (x>=y)
return recursiveGCD(y, x-y);
return recursiveGCD(x, y-x);
}
}
Code Analysis
iterativeMultiplication: How it works?
As of school days we know x * y means x * ( 1 + 1 + 1 + ... + 1 ) in which there are y ones in the parentheses and also we know that x * ( 1 + 1 + 1 + ... + 1 ) = x + x + x + ... + x . So in our for loop we add x to itself y times to obtain x * y .
As you see, the idea behind this method is very easy, straightforward and basic.
recursiveMultiplication: How it works?
As of high school days :) we remember x * y = x * ( 1 + y - 1 ) so x * y = x + x * ( y - 1 ) and remember that 1 is the identity element for multiplication which means x * 1 = x. Although I think this illustration is enough, let's investigate this method in more detail because Recursion is the subject of this article.
Consider the following code snippets:
public static void main(String[] args) {
System.out.println(Recursion.recursiveMultiplication(5, 3));
}
The process of executing is as follows:
!( 3 == 1 ) => return 5 + recursiveMultiplication(5, 2);
!( 2 == 1 ) => return 5 + [ 5 + recursiveMultiplication(5, 1); ]
( 1 == 1 ) => return 5 + [ 5 + [ 5 ] ] == 15
System.out.println(15);
iterativeFactorial: How it works?
As mentioned eaelier, n! = 1 * 2 * 3 * ... * n . So in for loop we declare a factorial variable initialized to 1. Then miltiply it to 1 , 2 , ... , n to obtain n!. No more discussion !
recursiveFactorial: How it works?
Using the relation n! = n * ( n -1 )!, in each step we reduce n till we reach 1. 0! in math is defined to be 1 and clearly 1! = 1 .
Consider the following code snippets:
public static void main(String[] args) {
System.out.println(Recursion.recursiveFactorial(6));
}
!( 6 ==1 ) => return 6 * recursiveFactorial(5);
!( 5 ==1 ) => return 6 * [ 5 * recursiveFactorial(4); ]
!( 4 ==1 ) => return 6 * [ 5 * [ 4 * recursiveFactorial(3); ] ]
!( 3 ==1 ) => return 6 * [ 5 * [ 4 * [ 3 * recursiveFactorial(2); ] ] ]
!( 2 ==1 ) => return 6 * [ 5 * [ 4 * [ 3 * [ 2 * recursiveFactorial(1); ] ] ] ]
( 1 ==1 ) => return 6 * [ 5 * [ 4 * [ 3 * [ 2 * 1 ] ] ] ] == 720
System.out.println(720);
iterativeFibonacci: How it works?
According to the definition of Fibonacci sequence, implementation of this method is very simple.
recursiveFibonacci: How it works?
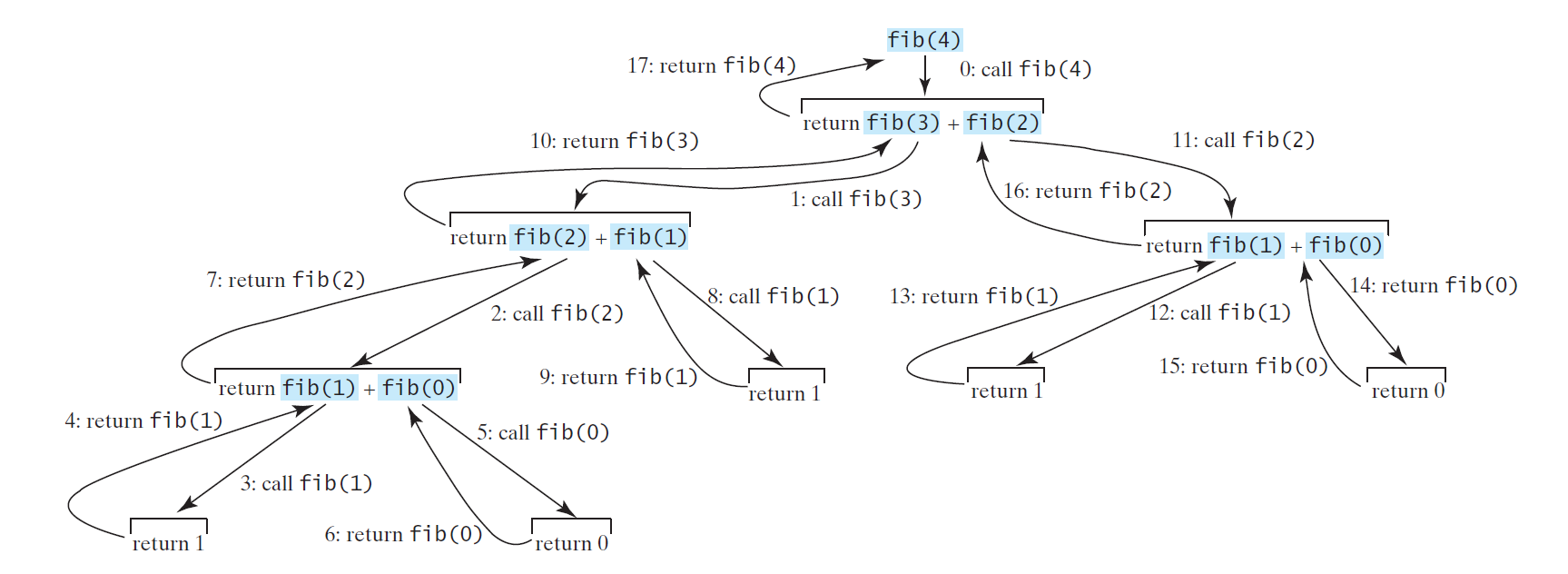
To illustrate this one, consider recursiveFibonacci(4); for example. Look at the following figure to understand the process of evaluation.
iterativeGCD: How it works?
In this method, we first set GCD to be 1. Since we know when m divides n, then m is less than or equal to n, we obtain minimum of our inputs. In for loop, we count from 1 to the minimum and as we find greater divisors, we change GCD to that.
recursiveGCD: How it works?
In this case, we're just using GCD properties such as gcd(m,n) = gcd(n,m) , gcd(m,1) = 1 , gcd(m,0) = m and the relation we mentioned earlier that if m is greater than or equal to n then gcd(m,n) = gcd(m-n,n) .
For example, consider the following code snippet:
public static void main(String[] args) {
System.out.println(Recursion.recursiveGCD(24, 12));
}
( 24 >= 12 ) => return recursiveGCD(12,12);
( 12 >= 12 ) => return recursiveGCD(12,0);
( 0 == 0 ) => return 12;
System.out.println(12);
Further Reading
I encourage you to search the web for following topics to extend your knowledge to Think Recursively :) :
- Tower of hanoi recursive algorithm in Java
- Reverse of a number using recursion in Java
- Selection sort using recursion in Java
- Binary search using recursion in Java
- Fractals using recursion in Java
The End --- Feel Free To Develop :)
