Introduction
You don't need to be an encryption-expert to encrypt your text in C# with this simple to implement Symmetric Encryption algorithm. The algorithm itself is very complex and secure, but using it is as simple as it can be.
Using the Code
Insert the class from the downloaded source code inside your namespace, and you will be able to instantiate objects of the class.
Encryption
The following code block is a short example of how to encrypt the string variable YourTextString with the encryption key variable YourEncryptionKey.
M3encryption.Key = YourEncryptionKey;
M3encryption objEncrypt = new M3encryption();
objEncrypt.ClearTekst = YourTextString;
objEncrypt.Encrypt();
if (objEncrypt.errorState > -1) {
MessageBox.Show(objEncrypt.EncryptedTekst);
}
Check the property objEncrypt.errorState for errors before proceeding in your code.
errorState -1:
This means the text encrypted contained characters outside of the UTF-16 range. These characters were changed to "?" in the cleartext before encryption.
errorState -2:
No encryption key was provided. The encryption process was aborted.
Decryption
M3encryption.Key = YourEncryptionKey;
M3encryption objEncrypt = new M3encryption();
objEncrypt.EncryptedTekst = YourTextString;
objEncrypt.Decrypt();
if (objEncrypt.errorState > -1) {
MessageBox.Show(objEncrypt.ClearTekst);
}
Randomization
Setting the property Randomization = true will produce a different cipher-text by the same key and clear text when run multiple times.
Randomization = false is default.
M3encryption.Randomization = true;
Fastmode
Setting the property Fastmode = true will make the encryption/decryption process faster, but also a little less secure. If you're encrypting small strings like passwords, card numbers, etc., you should not do it in Fastmode, but if you're encrypting documents like several pages long, you should do it in Fastmode.
Fastmode = false is default.
Notice! Decryption should be done in the same mode it was encrypted in.
M3encryption.Fastmode = true;
The Inner Workings of the Algorithm
General
The basic principle of this algorithm is character-remapping based on key self-mutation.
The lifespan of a key is equal to the length of the key. This means that any state of the key will only be responsible for encrypting a part of the clear-text that is equal in length to the length of that version of the key before the key is self-mutated into a new version. This new version will then encrypt the next part of the clear-text, etc.
In the overall process, you have a clear-key entered by the user which is diverted into 4 separate "threads" of different and constantly self-mutating keys. These 4 different keys are responsible for simultaneously converting the clear-text letters one letter at a time into cipher text by 2 different methods, these methods being: array remapping, and a sort of dynamic "substitution cipher". This whole process is repeated over and over again, re-encrypting everything a number of times before the cipher-text is finalized.
An attempt of reversing the process by a potential attacker would require figuring out the end state of 4 different keys simultaneously going backwards one mutation-version at a time. As 2 of these keys are used for array remapping, it is necessary to get the whole of these keys per letter decoded in the clear-text.
The bootstrap Process
As the algorithm uses self-mutating keys, it needs a bootstrap process to initiate the first encryption of the clear text key in a secure way. It's kinda like a "chicken or the egg" situation, in order to encrypt the key, it needs a mapping array which was produced by an encrypted key, but the key can't be encrypted without a mapping array. Alternatively, the mapping array could be produced by the clear text key, or it could be produced by a static hard-coded array, but that would make it a little less secure.
The bootstrap process consists of the following 4 steps:
- A mapping array will be produced by the cleartext key
- The cleartext key is encrypted by the mapping array
- A new mapping array is produced by the newly encrypted key
- A new key is encrypted by the newly created mapping array
The product will be a key encrypted by a mapping array which was produced by an encrypted key, and a mapping array for encrypting keys which was produced by an "unknown" encrypted key.
This is just the initial encryption of the key though, the key will self mutate multiple times throughout the entire encryption process. The mapping array for the "self-mutating inner key" will likewise be recreated multiple times before the final cipher-text is produced.
Outer and Inner Loops
The algorithm consists of an outer and inner loop. The outer loop iterates the rounds, the inner loop iterates the entire clear text one character at a time.
Self-mutating Outer and Inner Keys
The Self-mutating Inner Key
This key is used for encryption in the inner encryption process. Each letter of the key is used for encrypting the letter in the respective position in the clear text. When the key reaches the end of its string, the process will continue in a new mutated version of the key. This process will continue until the entire clear text string has been encrypted. See Figure 1 underneath for an illustration of this process. The self-mutating inner key is marked in blue.
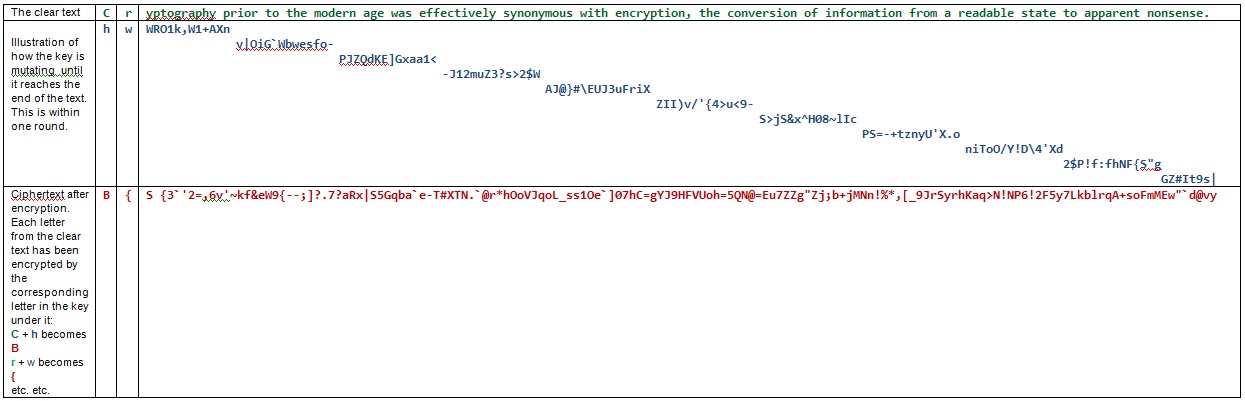
Figure 1. The key pattern in the above illustration will never repeat itself throughout the entire encryption process.
The Self-mutating Outer Key
The self-mutating outer key is initiated from the key entered by the user. This key is used in the outer loop and is self-mutated in the beginning of each round. The purpose of the key is to generate a unique mapping array for each round and to initiate the self-mutating inner key in these rounds. The mapping array is used by the encryption process in the inner loop.
Example of the key self-mutating in a 6 rounds iteration:
| Key entered by the user | xxxxxxxxxxxx |
| Round 1 | xX7IOiI:Ie7N |
| Round 2 | &8Xy4@obt $_W |
| Round 3 | 3cj`#sie391_?& |
| Round 4 | +sp=VGjHV>~tQ|C |
| Round 5 | J_fe2brc'3Rguxt^ |
| Round 6 | T2MV)X!CXV"2sUp{d |
History
- 20th December, 2015: Initial version
