Introduction
The following article demonstrates how to implement the Huffman adaptive algorithm. This algorithm provides the lossless compression for grayscale and 256 colors depth graphics images. The Huffman compression algorithm was invented by David A. Huffman in 1952. It is the most efficient compression algorithm with the minimal code redundancy. Initially, the Huffman compression algorithm was used by its inventor to compress datagrams transmitted as signals using cable or radio channels. Today, the Huffman adaptive algorithm is used as the "back-end" of "lossy" JPEG/MPEG compressors. It’s also used during RAR,ZIP,… achievers development. Since, it has been founded by D. Huffman, there’re basically two modifications of the following algorithm:
- Classical Huffman algorithm, in which, the encoding process is mainly based on using static fixed-length codes and building a Huffman tree;
- Huffman adaptive algorithm which is mainly based on using the variable-length symmetric codding, rather than building a Huffman tree during the encoding process;
Using the Huffman adaptive codding approach basically benefits in the decreasing of the amount of the encoded data. It’s providing the better compress ratio than the classical Huffman compression algorithm.
Background
The classical static Huffman encoding model is based on the characters frequencies that already estimated. The frequency of each character is estimated prior to the encoding process. Using the static model we firstly build the Huffman tree, obtain the appropriate codes from the tree and then encode each character from the input buffer. The following approach has two disadvantages:
- It’s necessary to view the encoded sequence of characters twice. It might cause the performance degrades;
- The entire Huffman tree and the frequency table must be passed into the decoder for correct decoding;
Therefore, we implement the Huffman adaptive algorithm which is based on using variable-length symmetric codes. It provides immediate data encoding without either building a Huffman tree or processing a sequence of characters more than once.
Typically, the Huffman adaptive algorithm has more cost-efficiency than the static Huffman encoding model and the other compression algorithms such as arithmetic or probability coding.
For instance, the Huffman adaptive algorithm is used in compact utility which is a part of UNIX operation system’s POSIX.
Note: The Huffman adaptive compression algorithm implementation, discussed in this article, can only be used to compress grayscale or 256 colors depth images or other multimedia files of an arbitrary file size, The files encoded should not be previously compressed using the other compression algorithms such as JPEG/MPEG/RAR/ZIP, etc.
Encoding data using the Huffman adaptive encoding algorithm
In this section we’ll demonstrate how to encode a string using Huffman adaptive algorithm. Suppose, we have the input characters buffer that’s containing a string – "ABBRRAAACCAADDAABBRAAA". This string is 23 bytes long. It consists of characters that occur in string more than once. We’d like to compress it using Huffman adaptive algorithm. To apply Huffman adaptive encoding to the string we normally need to iterate through the string of characters. We’re performing encoding for each character in string. The main idea of the Huffman adaptive algorithm the encoding starts with the "empty" Huffman tree, which
contains no entries for the characters. This tree will further be modified by appending the new characters and their codes. The Huffman tree should be modified similarly during the either encoding or decoding process. In both cases, we need to generate the same codes for each character from the input character buffer. Let’s recall, that during the Huffman adaptive encoding/decoding we actually don’t need to build a Huffman tree. We’re using the code generation method that allows to generate Huffman codes. But there’s one important limitation: when encoding the large amount of data, the code-space used for the codes generated by using the method describe below can gradually be exhausted. Remind that, we’re allocating just 8-bits (1 byte) code-space to generate the code for each encoded character. We are using linear left-shift bitwise operation "<<" to generate new code values. It’s possible to generate a code for only eight characters from the input buffer to be encoded. In this case, we have to perform the re-initialization of either the Huffman tree or characters frequency table.
At this point, let’s now have a short glance at the Huffman adaptive encoding process. As an example of the Huffman adaptive coding, we’ll encode first six characters from the string listed above. The first character of the following string is ‘A’=6510 = (01000001)2. This character’s ASCII code is represented as an 8-bit sequence. It is appended to the output buffer unencoded because at this point the Huffman tree is empty. Normally, the first character is appended to the Huffman tree and its code is initially assigned to 02. We have to append this character to the frequency table and assign the value of "1" to the character frequency counter variable associated with the given character. Finally, the output buffer will look as follows: 01000001 .In Huffman adaptive encoding algorithm we’re using the variable-length codes. It sometimes can be mistreated as unencoded characters of the 8-bit length. To avoid this collision, during the encoding process we have to use an escape-code. It’s represented as a certain sequence of bits. It’s appended to the output buffer before each unencoded character. The value of the escape-code, when encoding the first character ‘A’, is equal to "1". The next character retrieved from the input buffer is ‘B’. We’re performing the linear search in the Huffman tree to verify if the appropriate code for this character already exists in the Huffman tree. It indicates that the character has already been encoded. Normally, we’re performing the linear search for each character retrieved from the input buffer. If the current character doesn’t exists in the Huffman tree, the first what we have to do is to obtain the code for the character ‘B’ using the current value of escape-code ESC_CODE = 1. It can be done by performing the following bitwise operation: NEW_CODE = ESC_CODE << 1. In this particular case, the code for the character ‘B’ is NEW_CODE = 210 = 102 . After that, both the current escape-code and the unencoded character are appended to the output buffer. At this point we’ll have the following bits sequence in the output buffer: 01000001 1 01000010. The next, what we have to do is to append the new character along with its code NEW_CODE = 102 . It can be obtained above to the Huffman tree and calculate the new value of escape-code using the following bitwise operation: NEW_ESC_CODE = NEW_CODE + 1. Obviously, the new value of the escape-code is NEW_ESC_CODE = 310 = 112 . The next character is also the character - ‘B’, which already exists in the Huffman tree. In this case, we need to append the appropriate code to the output buffer. Obviously, the code for the character ‘B’ 102 , and the output buffer, in this case, contains: 01000001 1 01000010 10. We also need to increment the value of the frequency counter by "1" for the given character in the frequency table. The counter value for the character ‘B’ is "2". It means that the character ‘B’ occurred in the input buffer twice. Finally, we have to sort the frequency table by the value of characters occurrence frequency using quick sort algorithm. And then we have to modify the Huffman tree. The characters with the highest occurrence frequency are encoded using the codes of the minimum length. The codes having maximum length correspond to the characters with the lowest occurrence frequency. The next character retrieved from the input buffer is ‘R’. This character, also, occurred the first time and has no entry in the Huffman tree. Obviously we’re obtaining the code and escape-sequence for the following character using the method discussed above: NEW_CODE = 610 = 1102, NEW_ESC_CODE = 710 = 1112 . In this case, the output buffer will contain the following bits sequence: 01000001 1 01000010 10 11 01010010 . At the end of the encoding process the Huffman tree will contain the following character codes:
| character | frequency | code | escape-code |
| A | 2 | 02 | 12 |
| B | 2 | 102 | 112 |
| R | 2 | 1102 | 1112 |
There’re two more characters which we retrieve from the input buffer – ‘R’ and ‘A’. These two characters have already been encoded and the code for each character can be found in the Huffman tree. In this case R = 1102 , A = 02 . We’re appending these two codes to the output buffer. We’ll get the following sequence: 01000001 1 01000010 10 11 01010010 110 0. As the result of Huffman adaptive encoding, described above, we’ve obtained the following datagram:
ABBRRA (L = 48 bits) => 010000011010000101011010100101100 (L= 33 bits).
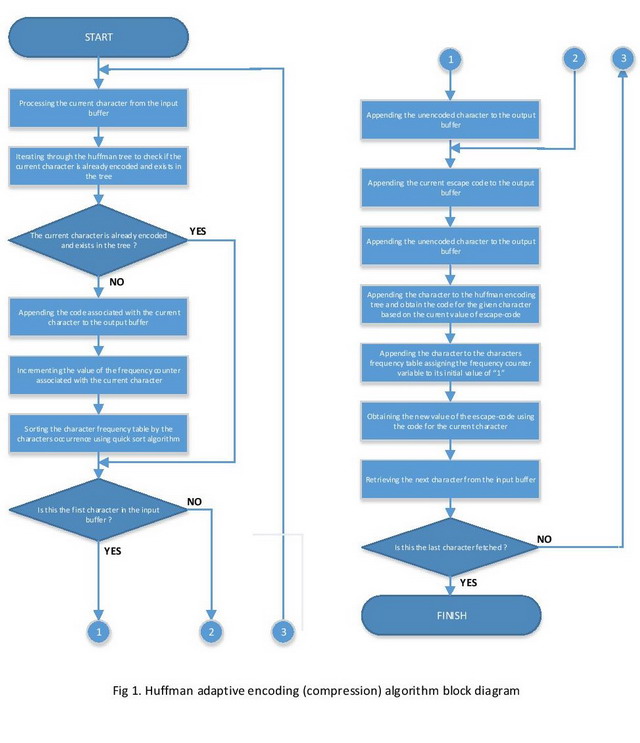
The block diagram that illustrates the process of Huffman adaptive encoding is shown on the Fig.1. As we can see from the output listed above, the Huffman adaptive coding is capable to encode a string of (6 bytes x 8 bits = 48-bits) length with the sequence of bits which is just 33-bits long. It means that the Huffman adaptive method also provides the data compression. The compress ratio of the Huffman adaptive coding can be evaluated using the following expression: \(r=1-\frac{L_{OUT}}{L_{IN}}=1-\frac{33}{48}\approx 1-0.69\approx 0.31\). According to the theory, classical static Huffman compression model algorithm ensures the compress ratio which is 0.27 using the fixed-length static codes during the data encoding process. Another benefit of the Huffman adaptive algorithm is that it doesn’t require to store the generated Huffman tree along with the encoded datagram contained in the output buffer. It allows to notably compact the amount of space used to store the encoded data.
In the next section of this article we’ll discuss the algorithm used to decode the data encoded using the Huffman adaptive algorithm. The output buffer for the following encoding algorithm is actually a sequence of bits. Each digit has its own absolute position. We need to append each bit or a portion of bits to the end of the controlled bits sequence using its absolute position in the current sequence. Unfortunately, in programming, there’s no a data structure that can be used to implement a sequence of bits. Either, there’re no operation that allow to set or modify a single bit. The most of the existing CPUs allow to process the data which is 1 byte = 8bits length. We’ll use an array of bytes to implement a bits sequence of a particular length. We need to implement a sequence of bits, which has the length of L = 48 bits. We’ll actually use an array of bytes, which size is 48/8 = 6 bytes long. Fig.2. illustrates a sequence of bits representation as an array of bytes.

Another, the most important aspect is implementing the routines to convert a bit’s absolute position into the bit’s position relative to a particular byte in the array of bytes. To do that, the first we have to locate the byte in the array by calculating the value of the byte’s index. We’re using the following expression, where is the bit’s absolute position. The all bits within a sequence are indexed in the reversible order. It means that the most significant bits belong to the first byte in the array. The least significant bits are located within the last byte. We need to modify the expression listed above by subtracting it from the total number of bytes allocated to store the sequence of bits _huff_buf_size. Finally, we’ll obtain the following expression, which is programmatically implemented as a C-macro (see the source code for more information how the following macro is used):
#define _huff_op_nbyte(nbit) ((_huff_buf_size-1)-nbit/(1<<3))
Suppose, if we have an absolute bit’s position equal to Nbit = 11 and the array size = 2 bytes, then we can calculate the byte’s index using expression above: ((2-1) – 11/8) = 1 – 1 = 0. That means, that the bit with absolute position located in the byte with the index Nbyte = 0 (first byte);
After that, we’ll have to calculate the relative position of a bit specified by using the following expression:
#define _huff_loc_nbit(nbit) ((_huff_bits-1)- \
(((_huff_bits*_huff_buf_size - 1) - (_huff_bits*_huff_op_nbyte(nbit))) - nbit)) \
- In this case, we’re calculating the highest position of a bit in a particular byte _huff_bits-1; For example (8-1) = 7;
- Then, We’re multiplying the number of bits within a byte by the total number of bytes the array contains. We’re doing it to find the highest absolute bit’s position within a sequence of bits. For example: (8 * 2 – 1) = 15;
- We’re multiplying the number of bits within a byte by the index of a byte to which the bit belongs and get the highest bit position which is relative to the byte to which the 11th bit belongs. In this case this value is equal to 0 = (8 * 0);
- We subtract the highest absolute bit’s position and the highest bit’s position relative to a byte and the position of bit specified to obtain the offset value with a particular bit;
- Finally, we subtract the value from the previous step from the highest bit position relative to a byte e.g. it’s equal to 7.
$ (8-1)-((8*2-1|8*((2-1)-11/8)|-11) = 3$
$ 7 – (15 – |8 * (1 – 1)) – 11|) = 3$
Decoding data using Huffman adaptive variable-length symmetric codes
Suppose, we have the datagram 01000001 1 01000010 10 11 01010010 110 0. It encodes a certain sequence of characters. Normally, we’ll treat this sequence as an input buffer and we iterate through the buffer represented as sequence of bits. For each bit or a portion of bits retrieved we’re performing the following decoding operation. The Fig.3 illustrates the Huffman adaptive decoding process. Initially, what we have to do is to retrieve the first eight bits from the datagram. This is a byte that represents an ASCII code of the character. It is placed at the beginning of the sequence unencoded. In this case, this is 010000012 = 6510 = ‘A’. Obviously this is the ASCII code of the character - ‘A’. At this point we’re appending this character to either the output buffer or the Huffman tree. Then We’re assigning the code associated with the following character to "0". Note, that at this time the output buffer will contain the following characters: OUTPUT = "A". Since, the Huffman tree was empty, this is the first character encoded. Also, we need to initialize the escape-sequence so that it’s equal to ESC_CODE = "1". The next, we retrieve the next 8th bit from the input buffer and append it to the temporary raw bits sequence. After that, we’re performing the check if the value of raw bits sequence is exactly matching the value of escape-code. If, so we’ll have to retrieve the next 8 bits from the input buffer. We have to treat it as the ASCII code of a certain character. Finally we append it to the Huffman tree by generating the appropriate code for this character. In this particular case, the value of the raw bits sequence is "1", which’s exactly matching the value of escape-code. We can retrieve the next 8 bits from the input buffer. Finally, we’ll get the ASCII code of the next character 010000102 = 6610 = ‘B’. We also append to the output buffer: OUTPUT = "AB". Similarly, we’re appending the character ‘B’ to the Huffman tree with new code obtained using the method described above: NEW_CODE = 210 = 102. Also, we need to recalculate the value of escape_code: ESC_CODE = 310 = 112. Finally, we have to flush the temporary raw buffer and proceed with the next bit, which has an index equal to 17.

We obviously need to append this bit to the raw buffer and check if it’s not equal to the value of escape-code. As we can notice, the value of escape code does not exactly match the contents of the raw buffer. Thus, we’ll have to perform the linear search in the Huffman tree to find the code that is equal to the value of the raw buffer. In this case, there’s no the appropriate code found in the Huffman tree. That’s why, we don’t perform any decoding so far. We’re appending the next 18th bit to the raw buffer. At this point the raw buffer will hold the following sequence of bits RAW_BUFFER = 102. We have to perform the similar check if this is not the value of escape-code ESC_CODE=112. In this case, it’s not, then we’ll perform the linear search in the Huffman tree. Finally, we’ve found the code 10, which maps to the character ‘B’, We’re appending the output buffer: OUTPUT = "ABB". Similarly we’ll retrieve 19th and 20th bits from the input buffer. We’re appending them to the raw buffer. In this case, this value is equal to the current escape-code value. We need to retrieve the next 8-bits sequence from the input buffer. This sequence is 010100102, which corresponds to the ASCII code of the character – ‘R’. We’re appending this character to the output buffer, which will contain the following string: OUTPUT = "ABBR". Obviously, we’re appending this character to the Huffman tree with code NEW_CODE = 610 = 1102. We’re retrieving each next bit from the input buffer. Finally will obtain the following value of the raw buffer RAW_BUFFER = 1102, which is the code of the character – ‘R’ in the Huffman tree. We’re appending this character to the output buffer. We’ll get the following string: OUTPUT = "ABBRR". Similarly, the next bit in the input buffer is ‘0’. This value obviously represents the code, which can also be found in the Huffman tree using linear search and the appropriate ASCII code can be obtained associated with the given character – 010000012=6510 = ‘A’. By appending this character to the output buffer we’ll get the final decoded string as follows: OUTPUT = "ABBRRA":
010000011010000101011010100101100 (L = 33 bits) => "ABBRRA" (L = 48 bits).
Points of interest
I’ve implemented the Huffman adaptive algorithm to use it to compress the 256 colors depth graphics images stored as BLOB-objects in large SQL production database to compact the space utilized to store the entire database. The implementation of the Huffman adaptive algorithm being discussed can also be used during the implementation of DEFLATE compression algorithm to provide the "back-end" compression for the LZ-family algorithms. Also, the Huffman adaptive algorithm can be used during the multimedia codecs such as JPEG and MP3 implementation.
