In this article, you will learn how to implement a neural network in VB.NET, namely, a model which is capable of processing input data and adjusting its internal mechanics to learn to produce a desired result.
Scope
In this article (hopefully, the first of a small series), we'll see how to implement a neural network in Visual Basic .NET, i.e., a model capable of processing input data and adjusting its internal mechanics to learn how to produce a desired result. We'll see more on this later. The present article will focus on generic definitions about neural networks and their behaviours, offering a simple implementation for the reader to test. In the final paragraph, we will code a small network capable of swapping two variables.
Introduction
A First Definition
The term "neural network" is typically used as a reference to a network or circuit constituted by neurons. We can differentiate two types of neural networks: a) biological and b) artificial. Obviously, speaking about software development, we are here referring to artificial ones, but those kind of implementations get their basic model and inspiration from their natural counterparts, so it can be useful to briefly consider the functioning of what we intend when we speak of biological neural networks.
Natural Neural Networks
Those are networks constituted by biological neurons, and they are typical of living creatures. The neurons/cells are interconnected into the peripheral nervous system or in the central one. In neurosciences, groups of neurons are identified by the physiological function they perform.
Artificial Neural Networks
Artificial networks are mathematical models, which could be implemented through an electronic medium, which mime the functioning of a biological network. Simply speaking, we will have a set of artificial neurons apt to solve a particular problem in the field of artificial intelligence. Like a natural one, an artificial network could "learn", through time and trial, the nature of a problem, becoming more and more efficient in solving it.
Neurons
After this simple premise, it should be obvious that in a network, being it natural or artificial, the entity known as "neuron" has a paramount importance, because it receives inputs, and is somewhat responsible of a correct data processing, which ends in a result. Think about our brain: it's a wonderful supercomputer composed by 86*10^9 neurons (more or less). An amazing number of entities which constantly exchange and store information, running on 10^14 synapses. Like we've said, artificial models are trying to capture and reproduce the basic functioning of a neuron, which is based on three main parts:
- Soma, or cellular body
- Axon, the neuron output line
- Dendrite, the neuron input line, which receives the data from other axons through synapses
The soma executes a weighted sum of the input signals, checking if they exceed a certain limit. If they do, the neuron activates itself (resulting in a potential action), staying in a state of quiet otherwise. An artificial model tries to mimic those subparts, with the target of creating an array of interconnected entities capable of adjusting itself on the basis of received inputs, constantly checking the produced results against an expected situation.
How a Network Learns
Typically, the neural network theory identifies three main methods through which a network can learn (where, with "learn", we intend - from now on - the process through which a neural network modifies itself to being able to produce a certain result with a given input). Regarding the Visual Basic implementation, we will focus only on one of them, but it's useful to introduce all the paradigms, in order to have a better overview. For a NN (neural network) to learn, it must be "trained". The training can be supervisioned, if we possess a set of data constituted by input and output values. Through them, a network could learn to infer the relation which binds a neuron with another one. Another method is the unsupervisioned one, which is based on training algorithms which modifies the network's weights relying only on input data, resulting in networks that will learn to group received informations with probabilistic methods. The last method is the reinforced learning, which doesn't rely on presented data, but on exploration algorithms which produce inputs that will be tested through an agent, which will check their impact on the network, trying to determine the NN performance on a given problem. In this article, when we'll come to code, we will see the first presented case, or the supervisioned training.
Supervisioned Training
So, let's consider the method from a closer perspective. What it means to train a NN with supervision? As we've said, it deals primarily with presenting a set of input and output data. Let's suppose we want to teach our network to sum two numbers. In that case, following the supervisioned training paradigm, we must feed our network with input data (lets say [1;5]) but also tell it what we expect as a result (in our case, [6]). Then, a particular algorithm must be applied in order to evaluate the current status of the network, adjusting it by processing our input and output data. The algorithm we will use in our example is called backpropagation.
Backpropagation
The backpropagation of errors is a technique in which we first initialize our network (typically with random values regarding the weights on single neurons), proceeding in forwarding our input data, matching results with output data we expect. Then we calculate the deviation of the obtained values from the desired one, obtaining a delta factor which must be backpropagated to our neurons, to adjust their initial state according to the entity of error we've calculated. Through trials and repetitions, several sets of input and output data are presented to the network, each time repeating the match between the real and the ideal value. In a certain time, that kind of operation will produce increasingly precise outputs, calibrating the weight of each network's components, and ultimately refining its ability to process the received data. For an extensive explanation about backpropagation, please refer to the Bibliography section.
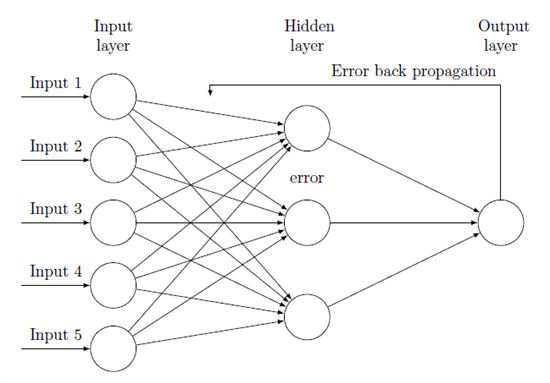
Creating a Neural Network
Now that we saw some preliminary concepts about neural networks, we should be able to develop a model which responds to the discussed paradigms. Without exceeding in mathematical over-explanations (which aren't really needed, unless you want to understand better what we will see), we will proceed step by step in coding a simple yet functional neural network, that we'll test when completed. The first thing we need to consider is the structure of a neural network: we know it's organized in neurons, and the neurons themselves are interconnected. But we don't know how.
Layers
And that's where the layers comes into scene. A layer is a group of neurons which share a more or less common function. For example, think about the entry point of input data. That will be the input layer, in which resides a group of neurons which share a common functionality, in that case limited to receiving and forward informations. Then we'll surely have an output layer, which will group those neurons that receive the result of previous processing. Among those layers could reside many layers, typically called "hidden", because a user won't have direct access to them. The number of those hidden layers, and the number of neurons each of them will contain, depends heavily on the natural and complexity of the problem we want to solve. To sum up, each network will be constituted of layers, each of which will contain a certain predetermined number of neurons.
Neurons and Dendrites
"Artificially" speaking, we could conceive a neuron like an entity which exposes a certain value, adjusted by trial iterations, and binded to other neurons through dendrites, which in our case will be represented by sub-entities possessing an initial random weight. The training process will consist of feeding the input layer neurons, which transmit their value through dendrites to an upper layer, which will do the same thing until the output layer is reached. Finally, we calculate a delta between the current output and the desired one, recurring through the network and adjusting the dendrites weights, the neuron values and each deviation value, to correct the network itself. Then we start again with another training round.
Preparing Network Classes
Having seen how a network is structured, we could sketch down some classes to manage the various entities of a network. In the following snippet, I will outline Dendrite, Neuron and Layer classes, which we will use together in the implementation of a NeuralNetwork class.
Dendrite Class
Public Class Dendrite
Dim _weight As Double
Property Weight As Double
Get
Return _weight
End Get
Set(value As Double)
_weight = value
End Set
End Property
Public Sub New()
Me.Weight = r.NextDouble()
End Sub
End Class
First, the Dendrite class: as you can see, it's constituted by a sole property, named Weight. In initializing a Dendrite, a random Weight is attributed to our dendrite. The type of the Weight property is Double, because our input values will be between zero and one, so we need a strong precision when it comes to decimal places. More on this later. No other properties nor functions are required for that class.
Neuron Class
Public Class Neuron
Dim _dendrites As New List(Of Dendrite)
Dim _dendriteCount As Integer
Dim _bias As Double
Dim _value As Double
Dim _delta As Double
Public Property Dendrites As List(Of Dendrite)
Get
Return _dendrites
End Get
Set(value As List(Of Dendrite))
_dendrites = value
End Set
End Property
Public Property Bias As Double
Get
Return _bias
End Get
Set(value As Double)
_bias = value
End Set
End Property
Public Property Value As Double
Get
Return _value
End Get
Set(value As Double)
_value = value
End Set
End Property
Public Property Delta As Double
Get
Return _delta
End Get
Set(value As Double)
_delta = value
End Set
End Property
Public ReadOnly Property DendriteCount As Integer
Get
Return _dendrites.Count
End Get
End Property
Public Sub New()
Me.Bias = r.NextDouble()
End Sub
End Class
Next, the Neuron class. As one can imagine, it will expose a Value property (of type Double, for the same motivations saw above), and a series of potential Dendrites, the number of which will depend to the neuron number of the layer our current neuron will be connected to. So we have a Dendrite property, a DendriteCount (which returns the number of Dendrites), and two properties which will serve in the process of recalibration, namely Bias and Delta.
Layer Class
Public Class Layer
Dim _neurons As New List(Of Neuron)
Dim _neuronCount As Integer
Public Property Neurons As List(Of Neuron)
Get
Return _neurons
End Get
Set(value As List(Of Neuron))
_neurons = value
End Set
End Property
Public ReadOnly Property NeuronCount As Integer
Get
Return _neurons.Count
End Get
End Property
Public Sub New(neuronNum As Integer)
_neuronCount = neuronNum
End Sub
End Class
Finally, a Layer class, which is simply a container for an array of neurons. In calling upon the New method, the user must indicate how many neurons the layer is required to have. We'll see in the next section how those classes can interact in the contest of a full-fledged neural network.
NeuralNetwork Class
Our NeuralNetwork can be seen as a list of layers (each of which will inherit the underlying layer properties, i.e., neurons and dendrites). A neural network must be launched (or put in running state) and trained, so we will likely have two methods which can be used for that means. The network initialization must specify, among other properties, a parameter that we will call "learning rate". That will be a variable we'll use in weights recalculation. As the name implies, the learning rate is a factor which determines how fast a network will learn. Since it's a corrective factor, the learning rate must be chosen accurately: if its value is too large, but there is a large multitude of possible inputs, a network may not learn too well, or at all. Generally speaking, a good practice is to set the learning rate to a relatively small value, increasing it if the effective recalibration of our network becomes too slow.
Let's see an almost complete NeuralNetwork class:
Public Class NeuralNetwork
Dim _layers As New List(Of Layer)
Dim _learningRate As Double
Public Property Layers As List(Of Layer)
Get
Return _layers
End Get
Set(value As List(Of Layer))
_layers = value
End Set
End Property
Public Property LearningRate As Double
Get
Return _learningRate
End Get
Set(value As Double)
_learningRate = value
End Set
End Property
Public ReadOnly Property LayerCount As Integer
Get
Return _layers.Count
End Get
End Property
Sub New(LearningRate As Double, nLayers As List(Of Integer))
If nLayers.Count < 2 Then Exit Sub
Me.LearningRate = LearningRate
For ii As Integer = 0 To nLayers.Count - 1
Dim l As Layer = New Layer(nLayers(ii) - 1)
Me.Layers.Add(l)
For jj As Integer = 0 To nLayers(ii) - 1
l.Neurons.Add(New Neuron())
Next
For Each n As Neuron In l.Neurons
If ii = 0 Then n.Bias = 0
If ii > 0 Then
For k As Integer = 0 To nLayers(ii - 1) - 1
n.Dendrites.Add(New Dendrite)
Next
End If
Next
Next
End Sub
Function Execute(inputs As List(Of Double)) As List(Of Double)
If inputs.Count <> Me.Layers(0).NeuronCount Then
Return Nothing
End If
For ii As Integer = 0 To Me.LayerCount - 1
Dim curLayer As Layer = Me.Layers(ii)
For jj As Integer = 0 To curLayer.NeuronCount - 1
Dim curNeuron As Neuron = curLayer.Neurons(jj)
If ii = 0 Then
curNeuron.Value = inputs(jj)
Else
curNeuron.Value = 0
For k = 0 To Me.Layers(ii - 1).NeuronCount - 1
curNeuron.Value = curNeuron.Value + _
Me.Layers(ii - 1).Neurons(k).Value * curNeuron.Dendrites(k).Weight
Next k
curNeuron.Value = Sigmoid(curNeuron.Value + curNeuron.Bias)
End If
Next
Next
Dim outputs As New List(Of Double)
Dim la As Layer = Me.Layers(Me.LayerCount - 1)
For ii As Integer = 0 To la.NeuronCount - 1
outputs.Add(la.Neurons(ii).Value)
Next
Return outputs
End Function
Public Function Train(inputs As List(Of Double), outputs As List(Of Double)) As Boolean
If inputs.Count <> Me.Layers(0).NeuronCount Or _
outputs.Count <> Me.Layers(Me.LayerCount - 1).NeuronCount Then
Return False
End If
Execute(inputs)
For ii = 0 To Me.Layers(Me.LayerCount - 1).NeuronCount - 1
Dim curNeuron As Neuron = Me.Layers(Me.LayerCount - 1).Neurons(ii)
curNeuron.Delta = curNeuron.Value * (1 - curNeuron.Value) * _
(outputs(ii) - curNeuron.Value)
For jj = Me.LayerCount - 2 To 1 Step -1
For kk = 0 To Me.Layers(jj).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(jj).Neurons(kk)
iNeuron.Delta = iNeuron.Value *
(1 - iNeuron.Value) * _
Me.Layers(jj + 1).Neurons(ii).Dendrites(kk).Weight *
Me.Layers(jj + 1).Neurons(ii).Delta
Next kk
Next jj
Next ii
For ii = Me.LayerCount - 1 To 0 Step -1
For jj = 0 To Me.Layers(ii).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(ii).Neurons(jj)
iNeuron.Bias = iNeuron.Bias + (Me.LearningRate * iNeuron.Delta)
For kk = 0 To iNeuron.DendriteCount - 1
iNeuron.Dendrites(kk).Weight = iNeuron.Dendrites(kk).Weight + _
(Me.LearningRate * Me.Layers(ii - 1).Neurons(kk).Value * iNeuron.Delta)
Next kk
Next jj
Next ii
Return True
End Function
End Class
New() Method
When our network is initialized, it requires a learning rate parameter, and a list of Layers. Processing that list, you can see how each layer will result in a generation of neurons and dendrites, which are assigned to their respective parents. Calling the New() method of neurons and dendrites, will result in a random assignation of their initial values and weights. If the passed layers are less than two, the subroutine will exit, because a neural network must have at least two layers, input and output.
Sub New(LearningRate As Double, nLayers As List(Of Integer))
If nLayers.Count < 2 Then Exit Sub
Me.LearningRate = LearningRate
For ii As Integer = 0 To nLayers.Count - 1
Dim l As Layer = New Layer(nLayers(ii) - 1)
Me.Layers.Add(l)
For jj As Integer = 0 To nLayers(ii) - 1
l.Neurons.Add(New Neuron())
Next
For Each n As Neuron In l.Neurons
If ii = 0 Then n.Bias = 0
If ii > 0 Then
For k As Integer = 0 To nLayers(ii - 1) - 1
n.Dendrites.Add(New Dendrite)
Next
End If
Next
Next
End Sub
Execute() Function
As we've said, our network must possess a function through which we process input data, making them move into our network, and gathering the final results. The following function does this. First, we'll check for input correctness: if the number of inputs are different from the input layer neurons, the function cannot be executed. Each neuron must be initialized. For the first layer, the input one, we simply assign to the neuron Value property our input. For other layers, we calculate a weighted sum, given by the current neuron Value, plus the Value of the previous layer neuron multiplied by the weight of the dendrite. Finally, we execute on the calculated Value a Sigmoid function, which we'll analyze below. Processing all layers, our output layer neurons will receive a result, which is the parameter our function will return, in the form of a List(Of Double).
Function Execute(inputs As List(Of Double)) As List(Of Double)
If inputs.Count <> Me.Layers(0).NeuronCount Then
Return Nothing
End If
For ii As Integer = 0 To Me.LayerCount - 1
Dim curLayer As Layer = Me.Layers(ii)
For jj As Integer = 0 To curLayer.NeuronCount - 1
Dim curNeuron As Neuron = curLayer.Neurons(jj)
If ii = 0 Then
curNeuron.Value = inputs(jj)
Else
curNeuron.Value = 0
For k = 0 To Me.Layers(ii - 1).NeuronCount - 1
curNeuron.Value = curNeuron.Value + _
Me.Layers(ii - 1).Neurons(k).Value * curNeuron.Dendrites(k).Weight
Next k
curNeuron.Value = Sigmoid(curNeuron.Value + curNeuron.Bias)
End If
Next
Next
Dim outputs As New List(Of Double)
Dim la As Layer = Me.Layers(Me.LayerCount - 1)
For ii As Integer = 0 To la.NeuronCount - 1
outputs.Add(la.Neurons(ii).Value)
Next
Return outputs
End Function
Sigmoid() Function
The sigmoid is a mathematical function known for its typical "S" shape. It is defined for each real input value. We use such a function in neural network programming, because its differentiability - which is a requisite for backpropagation - and because it introduces non-linearity into our network (or, it makes out network able to learn the correlations among inputs that don't produce linear combinations). Plus, for each real value, the sigmoid function return a value between zero and one (excluding upper limit). That function has peculiarities which make it really apt when it comes to backpropagation.

Train() Function
A network is initialized with random values, so - without recalibration - the results they return are pretty random themselves, more or less. Without a training procedure, a freshly started network can be almost useless. We define, with the word training, the process through which a neural network keeps running on a given set of inputs, and its results are constantly matched against expected output sets. Spotting differences on our outputs from the returned values of the net, we then proceed in recalibrating each weight and value on the net itself, stepping forward a closer resemblance of what we want and what we get from the network.
In VB code, something like this:
Public Function Train(inputs As List(Of Double), outputs As List(Of Double)) As Boolean
If inputs.Count <> Me.Layers(0).NeuronCount Or outputs.Count <> _
Me.Layers(Me.LayerCount - 1).NeuronCount Then
Return False
End If
Execute(inputs)
For ii = 0 To Me.Layers(Me.LayerCount - 1).NeuronCount - 1
Dim curNeuron As Neuron = Me.Layers(Me.LayerCount - 1).Neurons(ii)
curNeuron.Delta = curNeuron.Value * (1 - curNeuron.Value) * _
(outputs(ii) - curNeuron.Value)
For jj = Me.LayerCount - 2 To 1 Step -1
For kk = 0 To Me.Layers(jj).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(jj).Neurons(kk)
iNeuron.Delta = iNeuron.Value *
(1 - iNeuron.Value) * _
Me.Layers(jj + 1).Neurons(ii).Dendrites(kk).Weight *
Me.Layers(jj + 1).Neurons(ii).Delta
Next kk
Next jj
Next ii
For ii = Me.LayerCount - 1 To 0 Step -1
For jj = 0 To Me.Layers(ii).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(ii).Neurons(jj)
iNeuron.Bias = iNeuron.Bias + (Me.LearningRate * iNeuron.Delta)
For kk = 0 To iNeuron.DendriteCount - 1
iNeuron.Dendrites(kk).Weight = iNeuron.Dendrites(kk).Weight + _
(Me.LearningRate * Me.Layers(ii - 1).Neurons(kk).Value * iNeuron.Delta)
Next kk
Next jj
Next ii
Return True
End Function
As usual, we check for correctness of inputs, then start our network by calling upon the Execute() method. Then, starting from the last layer, we process every neuron and dendrite, correcting each value by applying the difference of outputs. The same thing will be done on dendrites weights, introducing the learning rate of the network, as saw above. At the end of a training round (or, more realistically, on the completion of several hundreds of rounds), we'll start to observe that the outputs coming from the network will become more and more precise.
A Test Application
In the present section, we will see a simple test application, which we'll use to create a pretty trivial network, used to swap two variables. In the following, we will consider a network with three layers: an input layer constituted by two neurons, an hidden layer with four neurons, and an output layer with two neurons. What we expect from our network, giving enough supervisioned training, will be the ability to swap the values we present it or, in other words, to being able to shift the value of the input neuron #1 on the output neuron #2, and viceversa.
In the downloadable NeuralNetwork class, you'll find a couple of methods which we haven't analyzed in the article, which refers to the graphical and textual network rendering. We will use them in our example, and you can consult them by downloading the source code.
Initializing the Network
Using our classes, a neural network can be simply initialized by declaring it, and feeding it its learning rate and start layers. For example, in the test application, you can see a snippet like this:
Dim network As NeuralNetwork
Private Sub Form1_Load(sender As Object, e As EventArgs) Handles MyBase.Load
Dim layerList As New List(Of Integer)
With layerList
.Add(2)
.Add(4)
.Add(2)
End With
network = New NeuralNetwork(21.5, layerList)
End Sub
I've defined my network as globally to a Form, then - in the Load() event - I've created the layers I need, passing them to the network initializator. That will result in having our layers correctly populated with the number of neurons specified, each element starting with random values, deltas, biases and weights.
Running a Network
Running and training a network are very simple procedures as well. All they require is to call upon the proper method, passing a set of input and/or output parameters. In case of the Execute() method, for example, we could write:
Dim inputs As New List(Of Double)
inputs.Add(txtIn01.Text)
inputs.Add(txtIn02.Text)
Dim ots As List(Of Double) = network.Execute(inputs)
txtOt01.Text = ots(0)
txtOt02.Text = ots(1)
Where txtIn01, txtIn02, txtOt01, txtOt02 are Form's TextBoxes. What we will do with the above code, is simply to get inputs from two TextBoxes, using them as inputs for the network, and writing on another couple of TextBoxes the returned values. The same procedure applies in case of training.

Swapping Two Variables
In the following video, you could see a sample training session. The running program is the same you'll find by downloading the source code at the end of the article. As you can see, by starting with random values, the network will learn to swap the signals it receives. The values of 0 and 1 must not be intended as precise numbers, but rather as "signals of a given intensity". By observing the results of training, you could note how the intensity of the values will increase toward 1, or decrease to zero, never really reaching the extremes, but representing them anyway. So, at the end of an "intense" training to teach our network that, in case of an input couple of [0,1] we desire an output of [1,0], we can observe that we receive something similar to [0.9999998,0.000000015], where the starting signals are represented, by their intensity, to the closer conducive value, just like a neuron behave himself, speaking about activation energy levels.
Demo video on YouTube:
https://www.youtube.com/embed/zymAdf_zMtQ
Source Code
The source code we've discussed so far can be download at the following link:
Bibliography
History
- 4th September, 2015: Initial version
