(If don't have the VS 2015 Redistributables, please find it here.)
Source code: available on GitHub.
Introduction - What are Hashes?
A hash function is defined as a function that maps data of arbitrary size to data of fixed size. Take the following picture as an example:
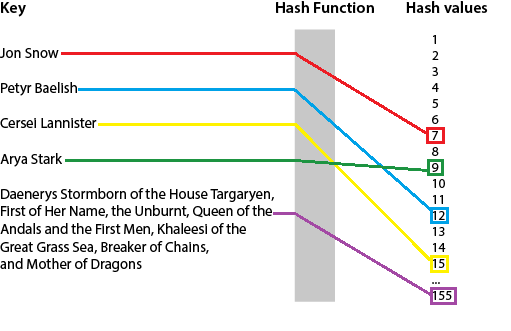
That is a hash function that maps names of arbitrary length to an integer. This hash function will simply count how many letters are in the name to find the correspondent integer. Note that, for this function, it is not hard to find examples of different keys that will be mapped into the same integer.
Some modern programming languages, like Ruby, have data structures called hash tables, which are used to implement dictionaries, which maps keys to values. These tables use hash functions to compute an index into an array of slots. Hash tables can be very efficient when used with a good hash function.
A cryptographic hash function is non-invertible, or, in other words, a one-way-function. This means that it is practically impossible to recreate the input of the function (normally called message), by looking only at the output of the function (called message digest).
Differently from regular hash functions, which also have some difficulty to be reversed, cryptographic hash functions are very hard to invert even if the attacker knows the theory and the algorithm used. Given only the hash, an attacker should have no clue about the original message, not even the size of the message (which, obviously, is not the case of the first example).
Besides that, cryptographic hash functions have the following characteristics:
- It is computationally easy to compute the hash value of any given message.
- Message integrity: It is not possible to modify the message without modifying the message digest.
- Collision resistance: It is infeasible to find two distinct messages that generate the same digest.
The most common hash functions are listed below:
- MD5: Announced in 1992 with a 128-bit digest size. Nowadays, it's considered cryptographically broken.
- SHA-1: Developed by NSA, was standardized in 1995. The digest size is 160-bit. It is no longer considered secure, new developments should implement SHA-2 or SHA-3 . Internet Explorer, Chrome and Firefox browsers have all announced they will stop accepting SHA-1 SSL certificates by 2017. On February, 2017, CWI Amsterdam and Google announced they found the first SHA1 collision, which, according to them, "emphasizes the necessity of sunsetting SHA-1 usage". We'll find prove that collision ourselves in the Practical Examples section.
- SHA-2: is a family of six cryptographic hash functions with four different digest sizes: 224-bit, 256-bit, 384-bit and 512-bit. Was also designed by the NSA and was published in 2001 as a U.S. federal standard (FIPS).
- The SHA-3 standard was released by NIST on August 2015.
Cryptographic hash functions play a major role on Public Key Cryptography, but in this article, we will examine their use in computing/verifying checksums.
Use of Cryptographic Hashes as Checksums
Downloading a File on the Internet
Many websites offering downloads provide the cryptographic hashes along with the downloadable files. For example, on Notepad++ download page, the user will find:

The author also makes a joke calling a paranoid anyone who would like to check the digests. Let's explain a little bit and let you decide whether or not it is paranoia to verify your downloads.
Listing the digests of the files serves two purposes:
- Security. If you download a file over the internet, perform a hash operation over this file and verify that the digest you calculated matches the one provided on the internet, you can be sure that the file you just downloaded is authentic, i.e., has not been tampered with. One could argue, though, that obtaining hashes from the same website you're getting the files is not especially secure because an attacker who has tampered with the file would probably also be capable of modifying the hash listing. Websites with a secured connection (HTTPS) and PGP-signed email from mailing list announcements are good places to get hash listings.
- Integrity. Hash values are good for detecting errors because the slightest modification on the original file over the transmission would generate a totally different digest. Only by looking at the digest, though, it is not possible to detect exactly what has changed, so the right action is to discard the downloaded file and start the download again.
This is what a list of checksums looks like:

Another Example - Downloading an Operating System
Perhaps you've decided that verifying every download you do is overzealous. If this is the case, no problem, it's up to you. But what about a very large file, or a very important one?
This is a screenshot of Ubuntu Vivid Vervet's download page. Along with various options of file formats for the download, there is always a list of the digests of such files.

Note that they are also offering SHA-256 sums, in accordance with the recommendation that new developments should use modern hash algorithms.
Transferring Files Via a Local Network or to External Media
If you have transferred files over a local network (maybe your company's intranet), you might have been familiar with the following message:

The first advice here is: do not cut & paste files over the network. Please, don't do that. I have seen several cases where, due to transmission errors, the file is cut from one machine and simply does not appear on the other end.
Instead of doing that, I advise you to copy the file to the remote machine and, after the transfer ends, hash the files both on the local and remote machines. If the digests match, you can now safely delete the original file. At work, we simply can't take chances of losing important files.
The same logic applies to your personal files. External hard drives are great for backing up your music, photos, videos, etc., but failures can occur, especially when we're talking about USB-powered devices. So, when in doubt if the transfer completed successfully, play safe and verify the digests.
Practical Examples
A little hands-on: as an example, let's download HxD, a really nice Hex Editor, and verify its digest. We are going to use the freeware #ashing, which has a simple graphical user interface on Windows.
This is what we find on the download page of the HxD:

After downloading the file, open your Downloads folder and find HxDSetupEN.zip.
Then, open #ashing and drag & drop the file into the program window. Alternatively, browse the file via the graphical interface.

Clink on the SHA-1 button to perform the hash operation:

Click 'Verify', then copy the digest found on HxD website and paste it on the new dialog that appears. Pay attention to not copy extra spaces after the end of the digest.

If everything went right, you shall see a confirmation that the digests match:

Proving the SHA-1 Collision
The SHAttered attack is explained here. As you can see, there are two PDF files available, very similar in form and content, the only difference being the background color:

Now, let's have a look at what happens when we calculate the digests for these two files applying different cryptographic hash functions. I have opened two instances of the #ashing application and calculated the digests:

You can see that the SHA-1 digests for both files is exactly the same. So, if two different (doesn't matter if they are similar) files have the same digest, it is proven in practice that the algorithm is broken.
It is interesting to notice, however, that the fact that these two files represent a collision in SHA-1 does not mean they will represent a collision in either less secure (MD5) or more secure (SHA-256, SHA-512) algorithms.
Use of Hashes in Blockchain
The term hash has become a buzzword since blockchain technologies have become more popular. Cryptographic hashes are, indeed, used for many purposes in blockchain implementations. In this section, we'll analyze some examples of how hashes are used in the bitcoin network.
Block Hash
If you're not familiar with the concept of a blockchain, check this visual guide from Reuters. The main ideas that I want you to understand are:
- A bitcoin transaction, which transfers some arbitrary amount from the holder of a cryptographic key to another, can be seen as a record;
- A block consists in a bundle of records and is created, in an average, every ten minutes;
- When a block is full, it's contents are hashed together with the hash of the preceding block, creating a chain.
The hash value of the block can be used to reference the block itself, as we can see in the following picture, taken from a block explorer:

For a more detailed explanation, I very much recommend the book Mastering Bitcoin, specially chapter 6.
Bitcoin Addresses
Abstraction
Bitcoin addresses are, in reality, an abstraction. Simply put, the act of sending coins to a bitcoin address means, under the hood, that you are allowing someone to spend a specific amount of coins if they are in possession of a specific private key.
There are different kinds of bitcoin addresses, but one of the most common is the P2PKH. Following that thought, a bitcoin transaction consists in using your private key to bind a certain amount of coins to a public key. Whoever possesses the corresponding private key will be able to spend those coins.
Why create an address instead of the public key itself? Besides favoring an abstraction, because not all bitcoin users are expected to know cryptography, there are a couple of things we can mention:
- Addresses are shorter, and bitcoin fees are based on the transaction size.
- By using the Base58Check encoding, addresses include a checksum that helps preventing transferring funds to the wrong person and they do not contain characters that look similar (like uppercase letter
o and the number zero, uppercase letter i and number one). Keep in mind that some users will keep their keys written down in paper.
Creating the Address
The description of bitcoin address creation can be seen in details here, but as a simplification, it is:
address = BASE58Check( RIPEMD160( SHA256(PUBLIC_KEY)) )
where RIPEMD160 and SHA-256 are cryptographic functions. The output of RIPEMD160 is 20 bytes. The final bitcoin address is typically 34 or 35 bytes long, which is way shorter than 65-byte-sized regular public keys.
Proof-of-Work
Proof-of-work is a mechanism to deter denial of service attacks and other abuses, like SPAM, by requiring some work from the service requester. It is by design that a block, in the Bitcoin blockchain, is created at an average of the minutes. In order for a block to be accepted by network participants, miners must complete a proof of work.
And guess what? The proof of work for Bitcoin consists on finding a hash value that starts with an arbitrary number of zeros. This is how it's done:
- Take the hash for the block (hash of all transactions in the block).
- Append an integer value to the end, called a nonce, starting with 0.
- Perform SHA-256 over this combination.
- If the result does not comply with the rules, increment the nonce and calculate again.
The difficulty determines how small the hashed value must be; in other words, with how many zeros it must start.
Utilities Available
On Linux (and many other Unix-like operating systems), there are a set of programs installed by default that perform cryptographic hashes: md5sum, sha1sum, sha224sum, sha256sum, sha384sum, sha512sum.
On Windows, there are no built-in checksum utilities. You can install OpenSSL for terminal-level operation or pick a graphical utility. Besides #ashing, there are many other options for calculating hashes. Gizmo's freeware has a detailed list of pros and cons of each.
On OS X, there is the built-in shasum command available in the terminal. To generate a SHA-512 hash of a file, for example:
shasum -a 512 /path/to/file
Let me know in the comments which utility you like the best, and why.
Code Snippets (C++)
Using OpenSSL
Pros: Open source, cross-platform, full-featured toolkit.
Cons: Must make sure that OpenSSL's crypto library is available at target computer, or the program won't run.
As stated above, you need to link your program against the crypto library.
Many Linux distros provide easy installation of OpenSSL via package manager (RPM, aptitude, YaST). After installation, simply add "-lcrypto" to your program's makefile.
An installer for Windows can be found here. The crypto library for Windows was formerly named libeay32.dll and, since version 1.1.0, OpenSSL have changed that library name to libcrypto.dll.
Start by including necessary headers (here is some documentation on SHA functions and MD5) and declaring a function to print the digest in the screen:
#include <stdio.h>
#include <string.h>
#include <openssl/sha.h>
#include <openssl/md5.h>
void printDigest(unsigned char* auchDigest, int iDigestSize)
{
for (int i = 0; i < iDigestSize; i++ )
{
printf("%02X", auchDigest[i]);
}
printf("\n");
}
When you already know the size of the data you're working with, it's quite simple:
void HashFromMemory( unsigned char* auchBufferToHash, int iBufferLen)
{
unsigned char auchDigest[64] = {0};
MD5(auchBufferToHash, iBufferLen, auchDigest);
printDigest(auchDigest, 16);
SHA1(auchBufferToHash, iBufferLen, auchDigest);
printDigest(auchDigest, 20);
SHA224(auchBufferToHash, iBufferLen, auchDigest);
printDigest(auchDigest, 28);
SHA256(auchBufferToHash, iBufferLen, auchDigest);
printDigest(auchDigest, 32);
SHA384(auchBufferToHash, iBufferLen, auchDigest);
printDigest(auchDigest, 48);
SHA512(auchBufferToHash, iBufferLen, auchDigest);
printDigest(auchDigest, 64);
}
When you do not know the size, or when the input might be very large, a good approach is to read the data in chunks:
void HashFromFile(const char* szFileToHash)
{
FILE* fp = NULL;
fp = fopen( szFileToHash, "rb");
if ( NULL == fp )
{
printf("Error opening file\n");
return;
}
fseek(fp, 0, SEEK_END);
long lSize = ftell(fp);
rewind(fp);
unsigned char btWorkBuffer[1024] = {0}; unsigned char auchDigest[64] = {0};
MD5_CTX ctx_md5;
SHA_CTX ctx_sha1;
SHA256_CTX ctx_sha224;
SHA256_CTX ctx_sha256;
SHA512_CTX ctx_sha384;
SHA512_CTX ctx_sha512;
if ( 1 != MD5_Init(&ctx_md5) || 1 != SHA1_Init(&ctx_sha1)
|| 1 != SHA224_Init(&ctx_sha224) ||
1 != SHA256_Init(&ctx_sha256) || 1 != SHA384_Init(&ctx_sha384)
|| 1 != SHA512_Init(&ctx_sha512) )
{
printf("Error initializing at least one context\n");
return;
}
int iRead = 0;
while ( iRead = fread(btWorkBuffer, 1, 1024, fp) )
{
if ( 1 != MD5_Update(&ctx_md5, btWorkBuffer, iRead)
|| 1 != SHA1_Update(&ctx_sha1, btWorkBuffer, iRead) ||
1 != SHA224_Update(&ctx_sha224, btWorkBuffer, iRead)
|| 1 != SHA256_Update(&ctx_sha256, btWorkBuffer, iRead) ||
1 != SHA384_Update(&ctx_sha384, btWorkBuffer, iRead)
|| 1 != SHA512_Update(&ctx_sha512, btWorkBuffer, iRead) )
{
printf("Error updating at least one hash\n");
return;
}
}
if ( 1 == MD5_Final(auchDigest, &ctx_md5) )
{
printf("MD5:"); printDigest(auchDigest, 16);
}
if ( 1 == SHA1_Final(auchDigest, &ctx_sha1) )
{
printf("SHA1:"); printDigest(auchDigest, 20);
}
if ( 1 == SHA224_Final(auchDigest, &ctx_sha224) )
{
printf("SHA224:"); printDigest(auchDigest, 28);
}
if ( 1 == SHA256_Final(auchDigest, &ctx_sha256) )
{
printf("SHA256:"); printDigest(auchDigest, 32);
}
if ( 1 == SHA384_Final(auchDigest, &ctx_sha384) )
{
printf("SHA384:"); printDigest(auchDigest, 48);
}
if ( 1 == SHA512_Final(auchDigest, &ctx_sha512) )
{
printf("SHA512:"); printDigest(auchDigest, 64);
}
}
And this is how it should be called:
int main(int argc, char* argv[])
{
unsigned char myBuffer[10] = {0}; HashFromMemory(myBuffer, sizeof(myBuffer));
HashFromFile("data.txt");
return 0;
}
There is also a higher-level approach, not only to perform hash operations but for cryptography in general, that uses an input-output abstraction called BIO. Here's an example of SHA-1 calculated that way.
