Introduction
The method of the least squares is a standard procedure to approximate a polynomial function to set reference points. The polynomial has a lower order n than the number of reference points. That leads to an overdetermined system of equations. If we have for instance a set of 7 reference points (x and y) and want to approximate a polynomial function of the 3. order, we can set up 7 equations like
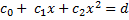
for 3 independent values. Leading to a Matrix equation
Cx = d
The method of the least squares searches for a polynomial function that leads to the smallest possible sum of the squares of the error of each equation. One approach to solve this problem is the use of the normal equation.
Normal equation
The Normal equation was used by Carl Friedrich Gauss to calculate the elliptic orbit of stars by their observation points. It introduces an error-vector r (the residual vector) into the Matrix equation from above:
Cx – d = r
And after a complicate calculation with transposed Matrixes, forward and backward substitution the solution is that the error vector becomes the smallest if

That means the both sides of the overdetermined Matrix equation from above have to be multiplied by the transposed Matrix of C. That leads to a n * n Matrix equation with n = order of the searched polynomial. This new Matrix equation can be solved and that yields the correct result in the vector x.
The multiplication by the transposed Matrix converts the overdetermined Matrix equation to a well determined system. In my example from above with 7 reference points and 3. Degree polynomial C has 7 lines and 3 columns. Multiplying it by its transposed makes a 3 x 3 Matrix of it and d becomes a 3 dimensional vector too. This Matrix equation can be solved by the elimination method of Gauss easily.
So the first step is to fill the Matrix equation. In C we have to put the x values of our reverence points. The first column of C consists of ones only as the first parameter we are looking for is c0 that is multiplied by 1. The second column gets x1…xn the third column (x1)^2…(xn)^2 and so on.
I defined a structure TMatrix containing C, x and d and created an instance m of this to work with. So
for (i = 0; i < samples; i++)
{
m.d[i] = y_k[i];
for (k = 0; k < order; k++)
{
m.c[i, k] = Math.Pow(x_k[i], k);
}
}
fills the Matrix equation
Now we have to multiply the equation by the transposed of C. The transposed Matrix of C is C mirrored at its main diagonal. In the sample the 3 x 7 Matrix becomes a 7 x 3 Matrix mirrored at the red marked main diagonal.
Now we have to multiply the equation by the transposed of C. The transposed Matrix of C is C mirrored at its main diagonal. In the sample the 3 x 7 Matrix becomes a 7 x 3 Matrix mirrored at the red marked main diagonal.
 =>
=> 
To multiply C^T with C the values 1 to n of a line of C^T have to be multiplied by the values 1 to n of a column of C and add together. So each value in the resulting matrix of the sample is the sum of 7 multiplications and we get a 3 x 3 matrix. The same is with d: The values of each line in C^T are multiplied by the values of d and add together. For this this we need a temporary Matrix a.
for (i = 0; i < order; i++)
{
a.d[i] = 0.0;
for (k = 0; k < samples; k++)
a.d[i] = a.d[i] + m.c[k, i] * m.d[k];
for (j = 0; j < order; j++)
{
a.c[j,i] = 0.0;
for (k = 0; k < samples; k++)
{
a.c[j, i] = a.c[j, i] + m.c[k,j] * m.c[k, i];
}
}
}
Calculates transposed(C) * C and transposed(C) * d and puts the result in a. The Matrix equation in a can be solved by Gauss now and we get the result in a.x[1] .. a.x[n].
Using orthogonal transformations
In the literature there is said that the use of the normal equation can lead to an inaccurate result. This is mainly caused by the multiplication of A * AT what can lead to a bad condition of the resulting matrix and due to that rounding errors can occur in the following operations. O.k. I have not experienced that so far but anyhow: The use of orthogonal transformations is an interesting approach :-)
Using orthogonal transformations means basically using rotation matrixes by Givens (see http://www.mosismath.com/RotationMatrix/RotationMatrix.html) and the basic idea is that the multiplication of a vector by an orthogonal matrix does not change the length of the vector and therefore the matrix equation with the residual vector
Cx – d = r
Can be transformed by these orthogonal matrixes without affecting the sum of the squares of the residua.
If we extend the main matrix C, which is a non-square n * m matrix, to get a square matrix and set the new elements all to 0 like:

the entire equation becomes
C’x – d = r
And can be multiplied by rotation matrixes to transform C’ into an upper triangle matrix without affecting the sum of the squares of the residua. That’s an important fact.
The transformation runs iterative. starting at element c21 the rotation matrix to eliminate this element in C’ is built, the multiplications are carried out and then the next rotation matrix is built to eliminate the next element c31 in C’ and so on, till we have the upper triangular matrix looking like:

This is done in a function:
public void RunGivens(int maxOrder)
{
int i, k;
for (i = 0; i < maxOrder; i++)
{
for (k = i + 1; k < maxOrder; k++)
{
if (m.c[k, i] != 0.0)
{
CalcRMatrix(i, k);
m.MultMatrix(r, i, k);
}
}
}
}
with
public void CalcRMatrix(int p, int q)
{
int i, j;
double radius;
radius = Math.Sqrt(m.c[p, p] * m.c[p, p] + m.c[q, p] * m.c[q, p]);
for (i = 0; i < m.size; i++)
{
for (j = 0; j < m.size; j++)
{
r.c[i, j] = 0.0;
}
r.c[i, i] = 1.0;
}
if (radius != 0.0)
{
if (m.c[p, p] == 0.0)
{
r.c[p, p] = 0.0;
r.c[p, q] = 1.0;
}
else
{
r.c[p, p] = m.c[p, p] / radius;
r.c[p, q] = m.c[q, p] / radius;
}
r.c[q, q] = r.c[p, p];
r.c[q, p] = -r.c[p, q];
}
}
That builds the upper triangular matrix in r.c
I marked all the elements which normally are not 0 in an upper triangular matrix but we are not interested in by “..” as these elements will become 0 in this case here anyway.
To build this upper triangular matrix we have to let p and q of the rotation matrix run from 1 to N basically. The vector d we have to multiply by the same rotation matrixes and principally r too. But as we are not really interested in r, we can leave that. Finally we have (in theory)
C’Qx – dQ = rQ
Or
C’’x – d’ = r’
With Q as the product of all rotation matrixes. If we have a look into the transformed C now, we can see that the elements in the rows 4 to 7 are all 0. That means the elements 4 to 7 of r’ are quite fixed as element 4 to 7 of d’.
We are looking for a solution of the matrix equation where the sum of the squares of the elements of r’ is the least. That’s the case when the elements 1 to 3 of r’ are 0.
That means we just have to solve this remaining matrix equation

by a backward substitution like
public void SolveRMatrix(int maxOrder, TMatrix mi)
{
int k, l;
for (k = maxOrder - 1; k >= 0; k--)
{
for (l = maxOrder - 1; l >= k; l--)
{
mi.d[k] = mi.d[k] - mi.x[l] * mi.c[k, l];
}
if (mi.c[k, k] != 0)
mi.x[k] = mi.d[k] / mi.c[k, k];
else
mi.x[k] = 0;
}
}
and then we are done :-)
Speed improvement
I made a small speed improvement here: In the sample from above, during transformation, we finally are interested in the elements of column 1 to m only as we are looking for a polynomial of the order m. If p is bigger than m, the multiplication by the rotation matrix only affects the elements in the rows bigger than m. So we can skip these multiplications and have p running only from 1 to m which is the order of the searched polynomial. That saves quit some calculation time. With this the function to transform the matrix C’ into an upper diagonal matrix looks like:
public void RunGivens(int maxP, int maxQ)
{
int i, k;
for (i = 0; i < maxP; i++)
{
for (k = i + 1; k < maxQ; k++)
{
if (m.c[k, i] != 0.0)
{
CalcRMatrix(i, k);
m.MultMatrix(r, i, k);
}
}
}
}
With maxP set to order and maxQ set to samples (see my sample project Smallest_Squares_Givens.zip).
Compared the method of the least squares it’s a completely different approach. Isn’t that fascinating? :-)
Using the code
My c# code sample contains just a main window. I implemented a class for the elimination method of Gauss to solve a Matrix equation and a function. On the top of the MainWin class the public const samples is defined to fix the number of satmples. This number of samples can be set between 4 and 40. In the Window there are 10 TextBoxes for x and y of max. 10 samples to be edited. If the number of samples is bigger than 10 this TextBoxes become invisible. In such a case the sample values must be initialized at application start. I implemented 7 sample points and initiate them in the function MainWin.
The order of the searched polynomial is defined on top of the MainWin class too. But order is not const. It can be changed between 1 and the number of samples in the application window in the right lower corner.
The application calculates the approximating function and draws it the function DrawGraph in the pGraph panel. For this it searches the maximum values in x and y direction and scales the graphic to fit into the panel. The reference points it draws as red dots. The polynomial is in a.x[0] to a.x[n].
