Introduction
XCode 5 released some cool compiler optimisations way back in 2013 (See this link for details). One of those features is auto-vectorization. I want to test how well this works in practise by comparing with some hand written assembler.
Background
Most ARM processors come with a NEON SIMD unit. This unit has 32 128 bit registers which can process 4 32-bit float operations in one cycle. Normally, to take advantage of the NEON unit you need to write assembly code, which is a pain. The auto-vectorization feature in the LLVM compiler in XCode is able to automatically convert standard c++ to NEON assembler.
Enabling auto-vectorization
In order to enable auto-vectorization you need to switch all the knobs on:
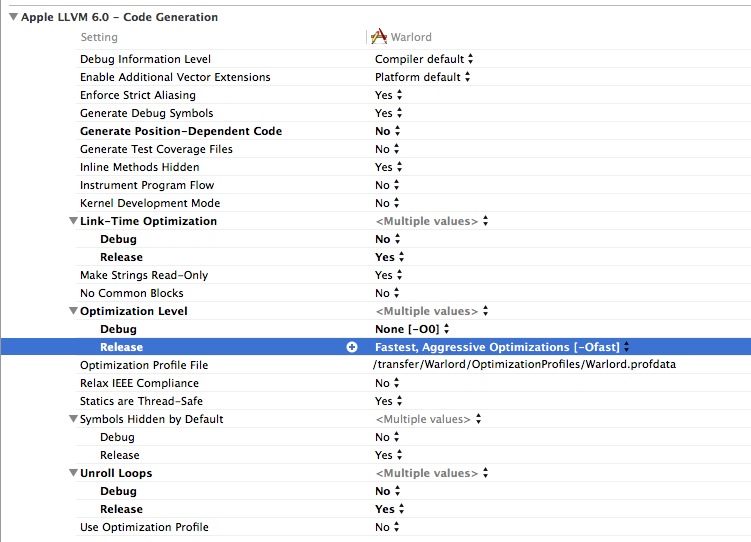
Enable "link time optimization", "Ofast", unroll Loops.
Matrix multiplication
I use a 4 x 4 matrix multiplication function for the benchmark test.
This is the code:
inline Matrix Matrix::operator*(const Matrix& matrix2) const
{
Matrix m3;
#ifdef USE_NEON
const float *pSelfMatrix = m;
const float *pMatrix2 = matrix2.m;
float* pOut = m3.m;
asm volatile (
"vld1.32 {d0, d1}, [%[pMatrix2]]! \n\t"
"vld1.32 {d2, d3}, [%[pMatrix2]]! \n\t"
"vld1.32 {d4, d5}, [%[pMatrix2]]! \n\t"
"vld1.32 {d6, d7}, [%[pMatrix2]] \n\t"
"vld1.32 {d16, d17}, [%[pSelfMatrix]]! \n\t"
"vld1.32 {d18, d19}, [%[pSelfMatrix]]! \n\t"
"vld1.32 {d20, d21}, [%[pSelfMatrix]]! \n\t"
"vld1.32 {d22, d23}, [%[pSelfMatrix]] \n\t"
"vmul.f32 q12, q8, d0[0] \n\t"
"vmul.f32 q13, q8, d2[0] \n\t"
"vmul.f32 q14, q8, d4[0] \n\t"
"vmul.f32 q15, q8, d6[0] \n\t"
"vmla.f32 q12, q9, d0[1] \n\t"
"vmla.f32 q13, q9, d2[1] \n\t"
"vmla.f32 q14, q9, d4[1] \n\t"
"vmla.f32 q15, q9, d6[1] \n\t"
"vmla.f32 q12, q10, d1[0] \n\t"
"vmla.f32 q13, q10, d3[0] \n\t"
"vmla.f32 q14, q10, d5[0] \n\t"
"vmla.f32 q15, q10, d7[0] \n\t"
"vmla.f32 q12, q11, d1[1] \n\t"
"vmla.f32 q13, q11, d3[1] \n\t"
"vmla.f32 q14, q11, d5[1] \n\t"
"vmla.f32 q15, q11, d7[1] \n\t"
"vst1.32 {d24, d25}, [%[pOut]]! \n\t"
"vst1.32 {d26, d27}, [%[pOut]]! \n\t"
"vst1.32 {d28, d29}, [%[pOut]]! \n\t"
"vst1.32 {d30, d31}, [%[pOut]] \n\t"
: [pOut] "+r" (pOut),
[pSelfMatrix] "+r" (pSelfMatrix),
[pMatrix2] "+r" (pMatrix2):
: "q0", "q1", "q2", "q3", "q8", "q9", "q10", "q11", "q12", "q13", "q14", "q15",
"memory"
);
#else
m3.m[0] = matrix2.m[0]*m[0] + matrix2.m[1]*m[4] + matrix2.m[2]*m[8] + matrix2.m[3]*m[12];
m3.m[4] = matrix2.m[4]*m[0] + matrix2.m[5]*m[4] + matrix2.m[6]*m[8] + matrix2.m[7]*m[12];
m3.m[8] = matrix2.m[8]*m[0] + matrix2.m[9]*m[4] + matrix2.m[10]*m[8] + matrix2.m[11]*m[12];
m3.m[12] = matrix2.m[12]*m[0] + matrix2.m[13]*m[4] + matrix2.m[14]*m[8] + matrix2.m[15]*m[12];
m3.m[1] = matrix2.m[0]*m[1] + matrix2.m[1]*m[5] + matrix2.m[2]*m[9] + matrix2.m[3]*m[13];
m3.m[5] = matrix2.m[4]*m[1] + matrix2.m[5]*m[5] + matrix2.m[6]*m[9] + matrix2.m[7]*m[13];
m3.m[9] = matrix2.m[8]*m[1] + matrix2.m[9]*m[5] + matrix2.m[10]*m[9] + matrix2.m[11]*m[13];
m3.m[13] = matrix2.m[12]*m[1] + matrix2.m[13]*m[5] + matrix2.m[14]*m[9] + matrix2.m[15]*m[13];
m3.m[2] = matrix2.m[0]*m[2] + matrix2.m[1]*m[6] + matrix2.m[2]*m[10] + matrix2.m[3]*m[14];
m3.m[6] = matrix2.m[4]*m[2] + matrix2.m[5]*m[6] + matrix2.m[6]*m[10] + matrix2.m[7]*m[14];
m3.m[10] = matrix2.m[8]*m[2] + matrix2.m[9]*m[6] + matrix2.m[10]*m[10] + matrix2.m[11]*m[14];
m3.m[14] = matrix2.m[12]*m[2] + matrix2.m[13]*m[6] + matrix2.m[14]*m[10] + matrix2.m[15]*m[14];
m3.m[3] = matrix2.m[0]*m[3] + matrix2.m[1]*m[7] + matrix2.m[2]*m[11] + matrix2.m[3]*m[15];
m3.m[7] = matrix2.m[4]*m[3] + matrix2.m[5]*m[7] + matrix2.m[6]*m[11] + matrix2.m[7]*m[15];
m3.m[11] = matrix2.m[8]*m[3] + matrix2.m[9]*m[7] + matrix2.m[10]*m[11] + matrix2.m[11]*m[15];
m3.m[15] = matrix2.m[12]*m[3] + matrix2.m[13]*m[7] + matrix2.m[14]*m[11] + matrix2.m[15]*m[15];
#endif
return m3;
}
(Note: I took the neon assembler code from here: http://math-neon.googlecode.com.)
This is how I ran the benchmark:
void PerfTests::TestMatrixMul2()
{
Matrix matrix1(1.0f, 1.01f, 1.02f, 0.03f,
1.01f, 1.011f, 1.012f, 0.13f,
1.02f, 1.021f, 1.022f, 0.23f,
0, 0, 0, 1.0f);
Matrix matrix2;
float angle[6];
angle[0] = -30.0f;
angle[1] = 160.0f;
angle[2] = 270.0f;
angle[3] = -30.0f;
angle[4] = 160.0f;
angle[5] = 270.0f;
matrix2.SetEulerXYZ(angle);
int n;
int timeNow = GetMilliSeconds();
for (n = 0; n < 5000000; n++)
{
matrix1 = matrix1*matrix2;
}
cout << endl;
matrix1.Dump(0);
int timeElapsed = abs(GetMilliSeconds()-timeNow);
cout << "total matrix multiply time: " << timeElapsed << "ms" << endl;
}
matrix2 contains serveral rotations and I am applying this rotation to matrix1 5 million times.
Results
I tested on a iPad Mini, which has a ARM Cortex-A9. Code was compiled with XCode 6.2 (which is old, I know, but I didn't have time to upgrade).
c++ version: 204 ms.
Neon verison: 855ms
That's more than 4 times slower for the hand coded neon version!
How, does it do this? I'm not sure, but I suspect that it's loading and saving the matrix into the neon registers only once outside the loop.
But before you jump to conclusions, I found some really wierd stuff going on when I ran these tests:
Firstly, by chance I added some extra code at the beginning TestMatrixMul2. This code was outside of the timed loop, so should not effect the result in any way whatsoever. However, it did. It caused the c++ version of the test to run twice as slow (ie. 431ms). It's still faster than the neon version, but it just shows how quirky the auto-vectorisation generation is.
Secondly, I tried disabling the "link time optimisation" setting. As expected this causes the c++ version to run much slower, but it also caused it to give a wrong result. This probably do to some rounding errors, but still it's rather worrying. (Note. I have "relax IEEE compliance" - aka fast math - switched off)
Thirdly, the function I used isn't that well optimised. You might notice it has a unnecessary object copy. I was able to get a more well optimised neon version running much faster (374ms).
Conclusion
Xcode's aggressive optimisations are very good, beating hand coded assembly under certain circumstances, however they are rather quirky. Making seemingly innocuous changes cause a 2x difference in performance. Also, they cause some issues with floating point accuracy.
