Introduction
Busy Healthcare facilities constantly face challenges due to the substantial increase in patient flow, costs associated with care providing to those patients and budget constraints. In order to aid decision-makers best utilize the available resources, application of modeling and simulation to the hospital operation was used to evaluate the efficiency of current strategy and predict the result of any future changes that might be applied to the system.
Models are mathematical frameworks that choose to represent some aspects of reality at a sufficient level of detail to facilitate estimation of the consequences of health care decisions and allow complex systems to be simplified to its essential elements. Models are considered essential tools in health technology assessment.
Simulation of a system is the computer based operation of a model, it makes it possible to study system properties, operating characteristics, evaluate different operational strategies, draw conclusions and make action decisions based on the results of the simulation before the actual implementation of the strategy is performed. It is useful tool that guides improvement of existing resources utilization strategy and assist in planning and designing new strategies based on data gathering and information technology.
Modeling process can be broadly divided into two distinct components:
1-Conceptualization of the problem:
Transform knowledge of the health care process into a simplified problem representation
2-Conceptualization of the model:
Direct the selection of modeling technique that satisfy needs of problem under investigation.
Moreover, nature of the problem under investigation, the target population, time horizon over which outcomes are represented, and the project objectives have substantial impact on model structure, required data to populate it, analytic perspective, and model reporting.
The experts in the health care system play a considerable role in problem conceptualization and developing model specifications. Initial conceptualization of the problem should provide a complete picture of the problem and not restricted by data availability. The Impact of missing or poor data quality on model structure should be evaluated through sensitivity analyses.
Many decision analysis models are available. The most basic form is the use of decision trees which are diagrams of all the possible scenarios a patient may go through and expected outcomes of each one at the end of the branch. The tree branches model all possible outcomes with their associated probabilities. Decision trees work well when outcome set is small and defined with short time horizon. In modelling chronic diseases such as cancer, parameters are not constant over time, the time-to-event plays an important role, and events may also recur. In these situations, Markov models are preferred. Markov models better handle long time horizons, timing of events, and recurring events.
Markov models are cohort-based models on which a hypothetical homogenous cohort of patients moves through defined states. Time is represented as cycles during which patients can (a) remain in their current health states, (b) move to another health state, or (c) move to a sink state (death), with certain transition probabilities.
During the simulation outcomes such as quality-adjusted life-years (QALYs) or costs can be accumulated in different strategies and then compared.
Although cohort-based models are relatively more simple, there are situations when individual-level outcomes must be represented. Moreover, markov models depends on the "Markovian assumption", which assumes that transition probabilities do not depend on history, which makes markov models "memoryless". This can be addressed by increasing the number of states. If the number of required states grows too large, individual simulation is a better alternative. It also allows better representation of heterogeneity in characteristics.

One approach to implement individual-level simulations is Discrete Event Simulation (DES), which is an adaptation of methods borrowed from engineering and operations research. DES represents the problem in defined states and events that can happen to individuals that transfer them from one state to another and consequences of those events.
Background
DES is the simulation technique of choice when:
• Model has very large numbers of states
• Competition for resources and queues formation need to be represented in the model to help improve service waiting times and answer resource allocation questions.
• There is a need to represent interactions between individuals in the model
Discrete Event Simulation models a system in order to compare different strategies and identify the one that best utilize the system under investigation. The core concepts of DES are entities, attributes, events, resources, queues and time. Entities are objects of interest (usually patients in health care models) that have attributes which influence the probability of experiencing certain events. They compete for the resources, and enter queues, over time.
Events may be a clinical condition such as relapse in cancer or resource use such as bed utilization that can occur, and recur, in any logical sequence. Queues formed by patients competing for resources can be represented by various service disciplines such as First in First Out or a Priority based discipline according to the discipline used in the system under investigation.
Discrete time handling nature of DES means that simulation moves forward in time at “discrete” points that events occur at. The model advance to next event, without unnecessary interim computations, which makes the DES computation much faster.
Stages of DES modeling process:
The first step in developing DES is to define the system under investigation and relevant events that can occur to individuals in that system. This is assisted by performing a model structure in which all possible scenarios and their required parameters are identified. The next step is to estimate those parameters using pre-collected data, if required data are not available or of a poor quality the expert in the system operation may be consulted for data elicitation and their responses should be validated. If expert elicited data are not of appropriate validity, the model should serve only as a guide for further data collection needed to build the model.
Model implementation involves transferring conceptual model structure into a computer program. Model can be populated and analyzed using DES dedicated software which may offer a better visualization of the problem through animations and also ease of application by a non-expert. Another approach is the use of a general programming language such as “R”.

General programing languages are more flexible in representing details of the system, provide shorter simulation running times and less dependence on commercial software. However, they don’t offer fancy animations and involve writing more code for package functions (such as: codes to formulate event list, queues formation, resources utilization and sampling from probability distributions) which makes its use more complex and requires extensive code debugging.
Model outputs may include mean values or distributions of values. Best practices recommends that the stability of output is considered acceptable if there is less than a 5% (or 1% according to the setting's threshold) difference between output values across model runs. Stability can be improved by running more entities, increasing time horizon or run more replications in one model according to the nature of system being simulated.
Validation techniques should be applied to ensure that the model accurately represents reality. Sensitivity analysis should be carried out to optimize the simulation model and identify variables which have significant impact on the model.
In DES reporting, both general and detailed representations of a DES structure and logic should be provided along with detailed event documentation figures as they are essential to the modeler when presenting the model methodology and results.
Using the code
First of all, you will need to install R and R-studio (R first, then R-studio). We used the package "r-simmer" to implement DES as clarified below. In this article we used r-simmer version 3.3. The full documentation of the package and dependencies installation is described in details here. The code attached to this article is to be run using R studio. One other option is to follow instructions of php script call described in this article, but the R script will need slight modifications that are also clarified in the "Enable calling though PHP" section below.
Assume you have a hospital with 30 inpatient beds allocated to accomodate patients of a specific disease. Let us assume that all patients accomodated will be treated by a standard protocol composed of 4 treatment phases. Before writing the code we started by drawing the decisions tree containing the probabilites, inter-arrival time (IAT), distributions and priorities of entities to compete for resources (beds in our case). A very simplified example is shown in the figure below. Practically, it can get much more complicated with nested branches and other add-on attributes.

About functions..
seize()
In our example, we used "bed" as resource. The function seize() will enable the entity (patient) to occupy a number of resources (in this example, one patient occupies one bed: amount=1). The priority here denotes that this entity will have priority rank when competing with other entities for the same resource. Priority 8 means that this entity will have priority over other entities with priorities 7 and less, but will not have priority over entities with priorities 9 or more.

timeout()
This function will return the amount of time that the entity will spend in a given state. So, if this function is used with seize(), this means that the entity will occupy the resource for the amount of time returned by this function.

In this example, the timeout() function will return one random value from normal distribution with a mean of 31.5 days and a standard deviation of 2 days.
Writing nested functions in "Human Readable" form
Instead of writing nested functions, the authors made use of the %>% (also known as: pipe) operator in R. For example if you have 3 nested functions, you will have two ways to write these functions: either the "classical" nested confusing form, or the understandable pipe form.
For example, if you have the following three functions..

Instead of writing a nested function like this..

We write it like this..

The code is heavily commented for clarification. In case you faced any challenges in implementation of the code, kindly leave a comment below and our team will respond as soon as possible.
cat("\014")
file.remove("envs.txt")
rm(list=ls())
nbeds<-30
myrep<-5
period<-730
myIAT<-3.65
NumGenPt<- 0
envs <- lapply(1:myrep, function(i) {
library(simmer)
env <- simmer("DiseaseX-env")
newpatient <- create_trajectory("DiseaseX_patient_path") %>%
set_attribute("health_attribute", function() rnorm(1,70,3))%>%
branch(function() sample(c(1,2),size=1,replace=T,prob=c(0.90,0.10)), continue=c(T, T),
create_trajectory("Treatment_Phase1") %>%
seize("bed", amount = 1, priority = 1) %>%
seize("Treatment_Phase1_in", amount = 1, priority = 1) %>%
timeout(function() rnorm(1, 31, 2)) %>%
release("bed", 1)%>%
set_attribute("health_attribute", function() rnorm(1,50,3))%>%
seize("gohome_after_Phase1", amount = 1, priority = 99) %>%
timeout(function() sample(c(4,5,6),1)) %>%
release("gohome_after_Phase1", 1)%>%
branch(function() sample(c(1,2),size=1,replace=T,prob=c(0.964,0.036)), continue=c(T, T),
create_trajectory("Treatment_Phase2") %>%
seize("bed", amount = 1, priority = 9) %>%
seize("Treatment_Phase2_in", amount = 1, priority = 9) %>%
timeout(function() rnorm(1, 28, 2)) %>%
release("bed", 1)%>%
seize("gohome_after_Phase2", amount = 1, priority = 99) %>%
timeout(function() sample(c(4,5,6),1)) %>%
release("gohome_after_Phase2", 1)%>%
branch(function() sample(c(1,2),size=1,replace=T,prob=c(0.752,0.248)), continue=c(T, T),
create_trajectory("Treatment_Phase3") %>%
seize("bed", amount = 1, priority = 8) %>%
seize("Treatment_Phase3_in", amount = 1, priority = 8) %>%
timeout(function() rnorm(1, 25, 2)) %>%
release("bed", 1) %>%
seize("gohome_after_phase3", amount = 1, priority = 99) %>%
timeout(function() sample(c(4,5,6),1)) %>%
release("gohome_after_phase3", 1)%>%
branch(function() sample(c(1,2),size=1,replace=T,prob=c(0.99,0.01)), continue=c(T, T),
create_trajectory("Treatment_Phase4") %>%
seize("bed", amount = 1, priority = 8) %>%
seize("Treatment_Phase4_in", amount = 1, priority = 8) %>%
timeout(function() rnorm(1, 31.5, 2)) %>%
release("bed", 1) %>%
seize("gohome_after_phase4", amount = 1, priority = 99) %>%
timeout(function() sample(c(4,5,6),1)) %>%
release("gohome_after_phase4", 1)%>%
branch(function() sample(c(1,2),size=1,replace=T,prob=c(0.2,0.8)), continue=c(T, T),
create_trajectory("relapse") %>%
seize("bed", amount = 1, priority = 8) %>%
seize("relapse", amount = 1, priority = 8) %>%
timeout(function() rnorm(1, 40, 2)) %>%
release("bed", 1)
,
create_trajectory("relapse_out") %>%
seize("relapse_out", amount = 1, priority = 1)
)
,
create_trajectory("Phase4_out") %>%
seize("Phase4_out", amount = 1, priority = 1)
)
,
create_trajectory("Phase3_out") %>%
seize("Phase3_out", amount = 1, priority = 1)
)
,
create_trajectory("Phase2_out") %>%
seize("Phase2_out", amount = 1, priority = 1)
)
,
create_trajectory("Phase1_out") %>%
set_attribute("health_attribute", function() rnorm(1,90,3))%>%
seize("phase1_out", amount = 1, priority = 1)
)
env %>%
add_resource("bed", nbeds) %>%
add_resource("Treatment_Phase1_in", Inf) %>%
add_resource("Treatment_Phase2_in", Inf) %>%
add_resource("Treatment_Phase3_in", Inf) %>%
add_resource("Treatment_Phase4_in", Inf) %>%
add_resource("relapse", Inf) %>%
add_resource("gohome_after_Phase1", Inf) %>%
add_resource("gohome_after_Phase2", Inf) %>%
add_resource("gohome_after_phase3", Inf) %>%
add_resource("gohome_after_phase4", Inf) %>%
add_resource("Phase4_out", Inf) %>%
add_resource("Phase3_out", Inf) %>%
add_resource("Phase2_out", Inf) %>%
add_resource("phase1_out", Inf) %>%
add_resource("relapse_out", Inf) %>%
add_generator("test_patient", newpatient, function() c(rexp(1, 1/myIAT), rep(0, NumGenPt)), mon=2)
env %>% run(until=period)
})
out <- capture.output(envs)
cat(paste(Sys.time(),"### Number of Bed =",nbeds,"### Number of Replica =",myrep,"### my IAT =",myIAT,"### Replicate Summary: \n"), out, file="envs.txt", sep="\n", append=TRUE)
attr<-envs %>% get_mon_attributes()
resources<-envs %>% get_mon_resources()
n_resources<-resources[resources$resource == "bed",]
arrivals<-envs %>% get_mon_arrivals(per_resource=T)
n_arrivals<-arrivals[arrivals$resource == "bed",]
n_arrivals$waiting <- n_arrivals$end_time - n_arrivals$start_time - n_arrivals$activity_time
n_arrivals$ALOS<-n_arrivals$activity_time
ALOS_n<-aggregate(n_arrivals$ALOS, by=list(n_arrivals$name), FUN=sum)
ALOS_n$x<-ALOS_n$x/myrep
arrivals_no_resource<-get_mon_arrivals(envs)
arrivals_no_resource$ALOS<-arrivals_no_resource$activity_time
arrivals_no_resource$waiting<-arrivals_no_resource$end_time - arrivals_no_resource$start_time - arrivals_no_resource$activity_time
filename_a<-paste0("arrival_",Sys.time(),".csv")
filename_a<-gsub(":", "_", filename_a)
write.csv(arrivals,filename_a)
filename_attr<-paste0("attributes_",Sys.time(),".csv")
filename_attr<-gsub(":", "_", filename_attr)
write.csv(attr,filename_attr)
filename_an<-paste0("arrival_no_res_",Sys.time(),".csv")
filename_an<-gsub(":", "_", filename_an)
write.csv(arrivals_no_resource,filename_an)
filename_r<-paste0("resources_",Sys.time(),".csv")
filename_r<-gsub(":", "_", filename_r)
write.csv(resources,filename_r)
r<-grep("\\brelapse\\b",out)
n<-grep('n_generated',out)
q<-grep("\\bbed\\b",out)
relapse<-out[r]
for (i in 1:myrep){
last<-regexpr('(Inf)', relapse[i])
relapse[i]= substr(relapse[i], (last-3), (last-2))
}
relapse<-as.numeric(relapse)
relapse
newpatients<-out[n]
for (i in 1:myrep){
last<-regexpr('}', newpatients[i])
newpatients[i]= substr(newpatients[i], (last-5), (last-2))
}
newpatients<-as.numeric(newpatients)
newpatients
queue<-out[q]
for (i in 1:myrep){
last<-regexpr('(Inf)', queue[i])
queue[i]= substr(queue[i], (last-4), (last-2))
}
queue<-as.numeric(queue)
queue
mydata<-data.frame(newpatients,relapse,queue)
write.csv(mydata, "my_log_data.csv")
library(gridExtra)
library(grid)
library(ggplot2)
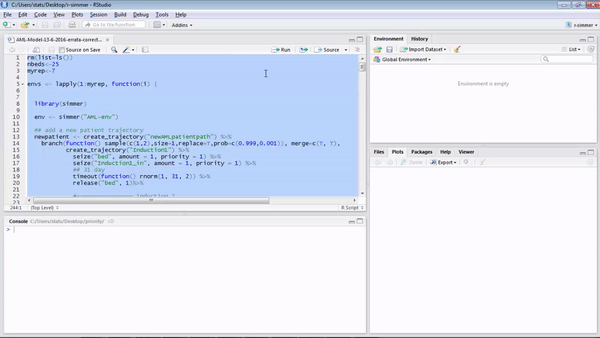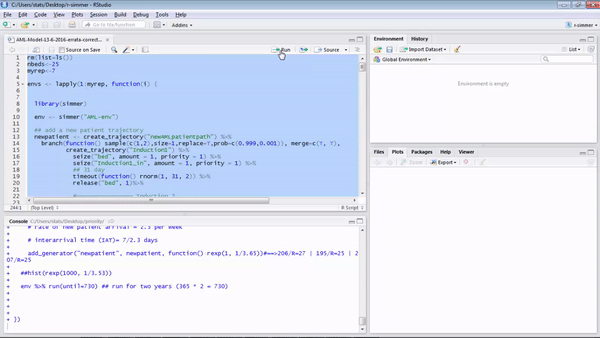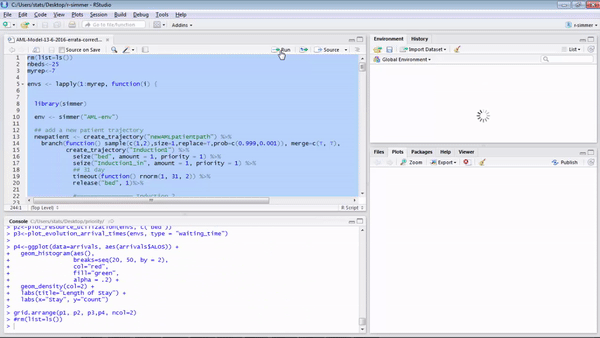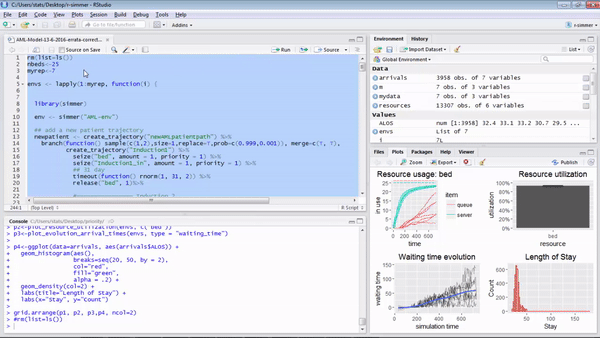
p1<-plot_resource_usage(envs, "bed", items = c("queue", "server"), steps = F)
p2<-plot_resource_utilization(envs, c("bed"))
p3<-plot_evolution_arrival_times(envs, type = "waiting_time")
p3<-p3 + geom_hline(yintercept=mean(arrivals_no_resource$waiting), colour="red", lwd=1)
p3<-p3 + geom_hline(yintercept=mean(n_arrivals$waiting), colour="green", lwd=1)
p4<-ggplot(data=n_arrivals, aes(n_arrivals$ALOS)) +
geom_histogram(aes(), breaks=seq(20, 50, by = 2), col="red", fill="green", alpha = .2) +
geom_density(col=2) +
labs(title="Length of Stay") +
labs(x="Stay", y="Count")
grid.arrange(p1, p2, p3,p4, ncol=2)
summary(n_arrivals$waiting)
summary(arrivals_no_resource$waiting)
if(myrep==1){
summary(ALOS_n$x)
}
summary(arrivals_no_resource$ALOS)
summary(n_arrivals$activity_time)
summary(n_resources$queue)
summary(mydata$newpatients)
Changing the variable myrep hwill run the simulation for a number of repetitions through the lapply().
myrep<-10 ## number of repetitions is 10 times

myrep<-100 ## number of repetitions is 100 times

myrep<-1000 ## number of repetitions is 1000 times

Enable calling through PHP
Calling R script using PHP is extremely simple. In this section we will describe few steps needed to call R script using PHP in Windows Environment. First Step is to create the R Script file MyModel.R containing the R script attached to this article. It is to be noted that by default files and images output by the model's script is saved to the working directory of R, which might not be accessible through web. So, running the R script through web will require slight modification in the code to save output in an accessible web folder. For example:
png(filename="c:/xampp/htdocs/model/output.png")
plot(MyDataPlot)
dev.off()
write.csv(MyData,"c:/xampp/htdocs/model/output.csv")
Next step is to create a batch file MyTask.bat containing one line as follows:
"C:\Rpath\R-3.2.3\bin\i386\Rscript.exe" MyModel.R
Keep in mind to replace the path and R version with the correct one on your machine.
We will finally need to call the MyTask.bat from a PHP file, but first we have to setup XAMPP server for Windows. Let's create RunScript.php and place it in a web folder.
<?php exec("MyTask.bat"); ?>
Once we access RunScript.php page through a web browser, the MyTask.bat will be triggered to run the R script MyModel.R and the output (csv files, logs and images) will be saved to the assigned web folder.
Acknowledgement
Many thanks to the authors of r-simmer Bart Smeets and Iñaki Ucar for their support.
Full R Package documentation is available here.
References
Modeling using Discrete Event Simulation: A Report of the ISPOR-SMDM Modeling Good Research Practices Task Force-4.
