High-performance finite elements with C#

Introduction

Open-source finite element (FE) codes are usually written in C++ and come as large libraries with thick user manuals. It is not surprising, because FE computations are complex and require high performance. Managed code was not intended to compete in performance with C, so languages like C# would be unlikely candidates for scientific computation. But is this the case with finite elements?

FE formulations exist for various models in thermodynamics, electromagnetism, continuum mechanics and other areas of physics. Most often they assemble and solve a linear system of equations \(\mathbf{\tilde{K} \tilde{u}=\tilde{f}}\), either once or multiple times. This step is the most computationally expensive, since the matrix \(\mathbf{\tilde{K}}\) is usually quite large.

Solving a linear system is an algorithmic problem, which has little to do with finite elements, so this taks is usually delegated to a separate algorithm. Therefore, the Finite Element code itself can be written in C#, making use of the managed collections and LINQ query operations with minimal memory fragmentation.

This article describes an implementation of an established technique in solid mechanics – linear static analysis. When external loads are applied to a deformable object, they create internal stresses and strains in the material, resulting in reaction forces and in deformation of the object. Static analysis determines the new equilibrium position and the new shape of the object. Such functionality is present in most commercial FE products and addresses real-life problems in structural engineering.

The included sample meshes are intentionally large and contain 100,000+ elements to benchmark the matrix assembly process. To crunch the linear system, a third-party linear solver is called, which is configured to use a CUDA-capable GPU or a CPU.

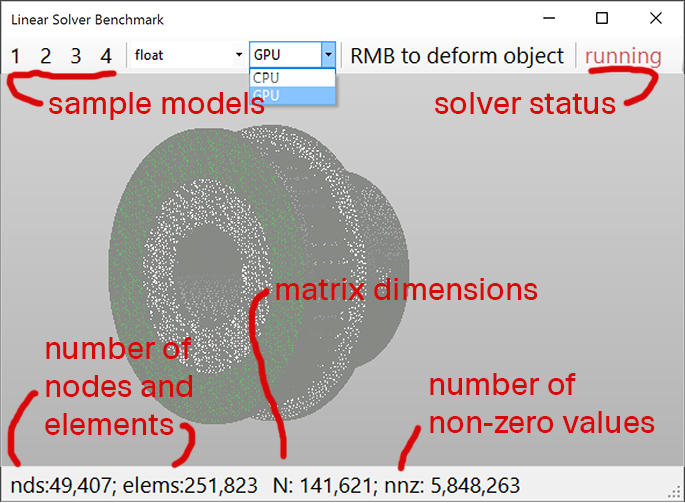
To test the enclosed demo, hold the right mouse button and move the mouse to deform the object. The solver will run as soon as the button is released. Rotate the sample with the left mouse button to view the results. When switching between samples the program may freeze for a few seconds to parse a mesh file.

Finite Element Method (FEM) for linear elasticity

In the finite element analysis, a deformable solid is represented by a mesh that consists of nodes, which keep track of their own displacements from the original locations (a so-called Lagrangian mesh). Tetrahedral elements allow a particularly simple formulation of the forces acting on the nodes. For each element, these forces are equal to:

Here, \(\mathbf{u}=\left[u_{x1},u_{y1},u_{z1},u_{x2},u_{y2},u_{z2},u_{x3},u_{y3},u_{z3},u_{x4},u_{y4},u_{z4}\right]{}^T\) is the 12-component displacement vector of the nodes, \(\mathbf{f}_{int}=\left[f_{x1},f_{y1},f_{z1},f_{x2},f_{y2},f_{z2},f_{x3},f_{y3},f_{z3},f_{x4},f_{y4},f_{z4}\right]{}^T\) is the 12-component vector of the resulting elastic forces, and \(\mathbf{K}\) is the so-called element stiffness matrix of size 12x12. The negative sign emphasizes the opposite direction of forces with respect to the direction of deformation (as when stretching a spring).

For a reader who is new to the topic, the size of the stiffness matrix (144 elements) may seem like a tremendous overkill. After all, for a spring model the relationship between forces and displacements is much simpler. But in a solid material a slightest deformation of any point in any direction creates internal forces in all directions in the whole object. The 12x12 stiffness matrix captures this complexity for each tetrahedral element. This type of elastic response is known as linear elastic model.

The linearity here means that the forces are linearly proportional to the displacements in each element as well as in the whole body. As a result, equations for each element can be additively combined together into one giant system of equations that describes the whole object:

where \(\mathbf{\tilde{u}}=\left[u_{x1},u_{y1},u_{z1},...,u_{zN}\right]{}^T\) is the combined displacment vector of all nodes (can be millions), \(\mathbf{\tilde{f}}_{int}=\left[f_{x1},f_{y1},f_{z1},...,f_{zN}\right]{}^T\) is the corresponding force vector of the same size, and \(\mathbf{\tilde{K}}\) is the global stiffness matrix of the size (3N)x(3N). An important observation here is that each new node adds 3 components to the displacement and force vectors, and 9 components to the global stiffness matrix.

For some meshes the matrix \(\mathbf{\tilde{K}}\) is so large that it does not fit into computer memory as a 2D array. Luckily, \(\mathbf{\tilde{K}}\) is a sparse matrix, having zeroes in most of its entries, which can be stored in the Compressed Sparse Row (CSR) format.

Up to this point it was not mentioned how the 12x12 element stiffness matrices are defined or calculated. They are expressed as the following product:

where \(V\) is the volume of the tetrahedral element, \(\mathbf{E}\) is the 6x6 elasticity matrix (see Hooke’s Law), and \(\mathbf{B}\) is the so-called strain-displacement matrix of size 6x12:

The coefficients \(a_1,a_2,a_3,a_4,b_1,b_2,b_3,b_4,c_1,c_2,c_3,c_4\) are found from the inverse of the Jacobian matrix of the tetrahedron:

where \(x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3,x_4,y_4,z_4\) are coordinates of non-displaced nodes of the tetrahedron. The derivation of the above relationships can be found in these lecture notes.

Finally, the following equilibrium equation defines the balance of internal and external forces:

where \(\mathbf{\tilde{f}}_{ext}\) is the vector of external forces, such as gravity, friction and external loads on the boundary. In the static problem, the equilibrium deformation is unknown. By solving the linear system, we obtain such deformation in which elastic response negates the external load. The force balance is written as:

Remark about the boundary conditions

In some mechanical problems, boundary conditions are formulated as prescribed displacements on certain parts of the object, e.g. a bridge that is fixed on two sides of a river. In the discretized model, components of \(\mathbf{\tilde{u}}\) that correspond to anchored nodes are constants, rather than unknown variables. To account for such case, the anchored nodes are removed from the linear system, and their effect on the remaining free nodes is accounted as an external force.

Compressed Sparse Row (CSR) format

As mentioned earlier, the resulting matrices are too large to fit in memory as 2D arrays. CSR is one of the common ways of storing sparse matrices. The matrix entries are described by 3 arrays:

public int[] rows, cols;  // structure of the sparse matrix
public double[] vals;      // non-zero values
public int N, nnz;

The size of the matrix is N*N, and the number of non-zero entries is nnz. The vals array holds only the non-zero elements listed left-to-right, top-to-bottom, and its size is nnz. The cols array holds column indices of the elements, hence its size is also equal to nnz. Lastly, rows contains indices of the first non-zero elements in each row. The size of the rows array is N+1, and rows[N] = nnz.

In this project, the sparse matrix is allocated along with the righ-hand side (RHS) of the linear system in the class CSR_System. The rhs vector is simply an array of size N. All real values are stored in double precision, but may be converted to single before being passed to solver.

Recap on matrix assembly

Steps to create the global stiffness matrix are:

1. For each node, find its neighbors.
2. List only nodes that are non-anchored and free to move around.
3. The number of unknown coordinates will be activeNodes.Count * 3. Number of non-zero entries of the matrix will be the total number of neighbors of active nodes multiplied by 9.
4. With the information from the previous step, allocate CSR arrays.
5. Iterate over all neighbors of active nodes, creating the structure (cols and rows) of the CSR matrix.
6. Iterate over all elements, assembling the elemental stiffness matrices into the global stiffness matrix and RHS.

After that, the system goes to solver.

Implementation

The finite element mesh is stored in two lists that reside in Model class:

public List<Node> nodes;
public List<Element> elems;

Nodes are scattered around with different values of 3D coordinates (x,y,z). Elements are 4-node tetrahedrons, where the points are stored in Node[] vertices. After the Model() constructor populates the nodes and elems, steps 1-5 are performed.

Creation of the CSR structure (steps 1-5)

At the heart of the process is the InitializeCSR() funciton. It begins by sequentially numbering the non-anchored nodes:

activeNodes = nodes.FindAll(nd => !nd.anchored);
int id = 0;
foreach (Node nd in activeNodes) { nd.altId = id++; }

At this stage, nodes "don't know" to which elements they belong. The next fragment of code populates the list of parent elements for each node:

foreach (Element elem in elems)
    foreach (Node nd in elem.vertices) nd.AddElem(elem);

Next, the nodes are ready to find their neighbors (adjacent nodes that are connected through the edges of the parent elements):

Parallel.ForEach(nodes, nd => nd.InferConnectivityInformation());

Neighbors are stored in HashSet<int>, where <int> corresponds to the index in activeNodes. Integer index in this case is better than a reference, because it will be subsequently used to create CSR sturcture. This step can be completed in parallel, since there are no write conflicts. 

In order to allocate the CSR, the total number of neighboring nodes are counted for active nodes:

int count = 0;
foreach (Node nd in activeNodes) count += nd.neighbors.Count;
csr = new CSR_System(activeNodes.Count * 3, count * 9);

At this point, the CSR is allocated, but has no structure. Hence, it is yet impossible to write any actual values into the matrix. We proceed by populatng the csr.cols and csr.rows. This step includes iterating over each neighbor of each active node, and creating 3x3 entries in the structure of the CSR matrix sequentially. Note that CreateCSRIndices(count, csr.cols) creates entries in the csr.cols array.

count = 0; // counts processed neighbors
foreach(Node nd in activeNodes) 
{
    int row_nnz = nd.CreateCSRIndices(count, csr.cols);
    csr.rows[nd.altId * 3] = count;
    csr.rows[nd.altId * 3 + 1] = count + row_nnz;
    csr.rows[nd.altId * 3 + 2] = count + row_nnz * 2;
    count += row_nnz * 3;
}

At this point, the CSR structure is created, and control is returned to GUI, where the user can modify the boundary conditions with a mouse. As soon as the right mouse button is released, AssembleLinearSystem() launches.

Assembling the matrix (step 6)

AssembleLinearSystem() implements the process outlined in the Finite Element section above. Its role is to distribute the element stiffness matrices into the global matrix. If this operation were done in parallel, write conflicts would occur. While parallel implementations exist for this step, overall performance benefit is marginal, considering that solving the system takes much more effort.

Assembly process is merely a nested loop:

foreach(Element elem in elems)
{
    double[,] K = elem.K; // element stiffness matrix of size 12x12
    for(int i=0;i<4;i++) 
        for(int j=0;j<4;j++)
        {
            // disperse the entries into CSR and RHS
        }
}

As soon as the assembling step is done, the resulting arrays are submitted to Paralution's preconditioned conjugate gradient solver via following function:

    [DllImport("SolverWrapperNativeCode.dll", CallingConvention = CallingConvention.Cdecl)]
    public static extern double solveCSRDouble(int[] row_offset, int[] col, double[] val,
int nnz, int N, double[] _rhs, double[] _x);

SolverWrapper configures Paralution and allocates appropriate objects. The return values are stored in _x[], then transferred to corresponding nodes for rendering. 

Final notes

The following libraries are required to build the project: Accord.NET, OpenTK and Paralution. In addition, CUDA Toolkit and ManagedCUDA are linked when using a CUDA device.

This project is not intended for actual FE analysis, but can serve as a starting point for writing a more advanced FE formulation, such as the corotational model, hyperelasticity, implicit dynamics, plasticity and remeshing. Readers are encouraged to experiment with other solvers that use CSR format, such as PETSc. 

Solution times are highly variable even for a same mesh. On a desktop machine, the solver easily handles matrices with 30+ million non-zero entries, both on a CPU and on a GPU.

Versatile libraries that are available for C# come extremely handy for performing scientific computations. For example, the element stiffness matrix is initialized in (almost) a sigle line:

K = B.TransposeAndMultiply(E).Multiply(B).Multiply(J.Determinant() / 6D); // K = (Bt x E x B)*V

While the above code is qiute slow (especially comparing to CUDA implementations), for rapid error-free scientific computing, simplicity beats efficiency.

Source and Demos

The project and demos are available on GitHub. Due to their lage size, .geo meshes and CUDA libraries are zipped individually. Just unpack all files to run the demo.