This article presents how to implement a well-known agglomerative clustering algorithm in C#.
Introduction
Finding a data clustering in a data set is a challenging task since algorithms usually depend on the adopted inter-cluster distance as well as the employed definition of cluster diameter.
This article describes how to use and implement a well-known agglomerative clustering algorithm named AGNES using the C# programming language. Such algorithm and all the code presented in this article was incorporated in this project: https://github.com/rodrigocostacamargos/SharpCluster.NET
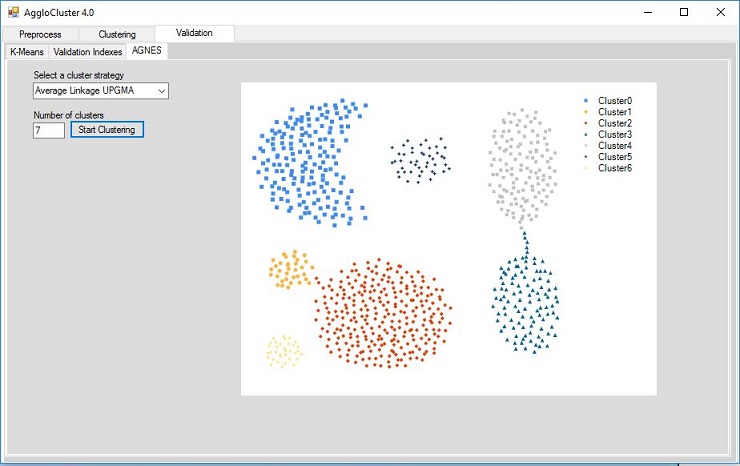
Figure 1. AggloCluster
AggloCluster (Figure 1) is a Windows Form application that enables users to execute clustering algorithms provided by the SharpCluster.NET library. We will be using this application in order to execute the agglomerative clustering algorithm described in this article. Its source code can be found in https://github.com/rodrigocostacamargos/AggloCluster.NET.
IMPORTANT: Only the code (and its dependencies) described in this article is available to download (SharpCluster.zip). If you want to explore all AggloCluster functionalities, you have to download it from AggloCluster/Cluster.NET project on Github.
Background
Machine Learning (ML) is a subfield of Artificial Intelligence (AI) focused mainly on investigations and proposals of new formalisms and computational algorithms, aimed at proving theoretical support as well as implementing automatic learning by computers. Over the past few decades, many ideas on how to enable automatic learning have been presented, discussed and implemented. Among the many ways ML can be implemented, the so called clustering algorithms are a particular group of (unsupervised) algorithms which aims at organizing sets of data points into groups, having data exploratory processes in sight. In the literature, one can find numerous works proposing new clustering algorithms as well as different clustering taxonomies. Although taxonomies aim at organizing such algorithms into categories, due to the fact that usually they adopt different criteria for grouping them, they are not necessarily, compatible with each other.
Efficient clustering techniques are considered a challenge, mainly due to the fact that there is no external supervision, which implies knowing nothing about the internal structure of point sets (such as spatial distribution, volume, density, geometric shapes of clusters, etc.). In such a scenery, automatic learning becomes an exploratory task, aiming at identifying which are the groups of data points that are statistically separable (or not), which are the most obvious clusters and how they relate to what is aimed at to discriminate, in an attempt to expose the underlying structure of the data, based only on their descriptions, generally given as a vector of attribute values.
In a simplistic way, clustering algorithms try to find groups of data points such that the data points in a group will be similar (or related) to one another and different from (or unrelated to) the data points in other groups. The similarity concept adopted by the clustering algorithm described in this article is a proximity measure defined by the Euclidian distance between two data points (Pi and Pj).

So the main goal of a clustering algorithm is to minimize intra-cluster distances and maximize inter-cluster distances, as shown in Figure 2.

Figure 2. Distance between data points in the same cluster and distance between data points in different clusters. Image extracted from Tan, Steinbach and Kumar slides.
In order to get a better intuition of what clustering really means and what a clustering algorithm does, the section Using the Code explains how to use AggloCluster and SharpCluster.NET library to perform a clustering task. You will be expected to get some clustering results, as shown in figures 3 and 4, while understanding the code behind it.

Figure 3 - Clustering result on Aggregation dataset (Average Linkage UPGMA clustering strategy).

Figure 4 - Clustering result on Smile dataset (Single Linkage clustering strategy).
Figures 3 and 4 show the clustering results on data sets, Aggregation.arff and Smile.arff, respectively. Those data set files are available in the AggloCluster.zip file. The clustering strategies (Single Linkage, Complete Linkage and Average Linkage) used by the agglomerative algorithm to produce that result is described in the next section.
The AGNES (AGglomerative NESting) Algorithm
For a given data set containing N data points to be clustered, agglomerative hierarchical clustering algorithms usually start with N clusters (each single data point is a cluster of its own); the algorithm goes on by merging two individual clusters into a larger cluster, until a single cluster, containing all the N data points, is obtained. Obviously, the algorithm can have another stopping criteria, such as that of ending when a clustering containing a user-defined number of clusters (k) is obtained.
Figure 5 presents a high level pseudocode of the AGNES algorithm which, at each iteration, chooses two clusters to be merged, based on the shortest Euclidean distance between the clusters formed so far. The many clustering agglomerative algorithms found in the literature can be organized taking into account the way the inter-cluster distance is defined, i.e., what definition is used to compute the shortest distance between all pairs of clusters. Among the various ways, three are particularly popular and are defined next. Given two clusters, X and Y, let d(x,y) denote the distance between two data points.
(1) Single Linkage, the distance between two clusters X and Y is the shortest distance between two data points, x belongs to X and y belongs to Y, formally represented by Eq. (1).

(2) Complete Linkage, the distance between two clusters X and Y is the farthest distance between two data points, x belongs to X and y belongs to Y, formally represented by Eq. (2).

(3) Average Linkage, where the distance between two clusters is the mean distance between data points of each cluster in one cluster to every point in the other cluster, formally represented by Eq. (3).


Figure 5. A customized version of AGNES pseudocode
To find the closest pair of clusters (i.e., min distance), AGNES looks for the lowest distance value in the dissimilarity matrix. The dissimilarity matrix (DM) is always updated because the algorithm, at each iteration, merges the closest pair of clusters into a new cluster and such cluster is a new entry of the matrix. More formally, at each level, t, when two clusters are merged into one, the size of the dissimilarity matrix DM becomes (N - t) x (N - t). DMt follows from DMt-1 by (a) deleting the two rows and columns that correspond to the merged clusters and (b) adding a new row and a new column that contain the distance between newly formed clusters and the old clusters.
The matrix update procedure described before may sound confusing, but understand the code that implement it is not that hard as you will see in the next section. So to clear your mind about how a dissimilarity matrix looks like, see tables 1 and 2.

Table 1. Data set matrix

In order to get the values shown in Table 2, AGNES calculates the Euclidian distance for all data points presented in Table 1.

Table 2 - Dissimilarity matrix
Looking at the dissimilarity matrix, you will see that the lowest distance value is 0.41 (not considering the diagonals elements) and AGNES would start merging data points 2 and 4, forming a new cluster.
Using the Code
In this section, we will be using AggloCluster to execute the AGNES algorithm implementation that is provided by the SharpCluster.NET library. So, first download SharpCluster.zip, extract the files and compile the source code (it will generate new SharpCluster.dll and SharpCluster.pdb files). Second download AggloCluster.zip, extract the files and replace SharpCluster.dll and SharpCluster.pdb with the new ones. In sequence, execute AggloCluster.exe and do the following steps:
- On the Preprocess tab, click in Open file and select any of the dataset files that came with AggloCluster.zip file;
- Next, click on the Validation tab and then click on the AGNES tab;
- In sequence, select one of the four clustering strategies from the drop-down list;
- Enter the number of clusters (COP.arff has three clusters, Aggregation.arff has seven clusters and Simle.arff has four clusters);
- Finally, click the Start clustering button. Clicking the Start clustering button will execute the
ExecuteClustering method. (In case you want debugging, open SharpCluster.csproj in Visual Studio and attach the AggloCluster process to it).
As mentioned before, the first method to be called by the AggloCluster is the ExecuteClustering located in the Agnes class of the SharpCluster.csproj.
public Clusters ExecuteClustering(ClusterDistance.Strategy strategy, int k)
{
this._BuildSingletonCluster();
this._BuildDissimilarityMatrixParallel();
this.BuildHierarchicalClustering(_clusters.Count(), strategy, k);
return _clusters;
}
After creating the initial clustering formed by singleton clusters (Step 1), the dissimilarity matrix, which contains all the distances between all pair of clusters, is built (Step 2) by performing all the computation needed in parallel. Such computation could be performed sequentially; however, I found feasible to implement it concurrently in order to improve the overall algorithm's performance.
private void _BuildDissimilarityMatrixParallel()
{
double distanceBetweenTwoClusters;
_dissimilarityMatrix = new DissimilarityMatrix();
Parallel.ForEach(_ClusterPairCollection(), clusterPair =>
{
distanceBetweenTwoClusters =
ClusterDistance.ComputeDistance(clusterPair.Cluster1, clusterPair.Cluster2);
_dissimilarityMatrix.AddClusterPairAndDistance
(clusterPair, distanceBetweenTwoClusters);
});
}
The method _ClusterPairCollection just build the collection of cluster pair. The pair of clusters and the distance are the entries of the dissimilarity matrix.
private IEnumerable<ClusterPair> _ClusterPairCollection()
{
ClusterPair clusterPair;
for (int i = 0; i < _clusters.Count(); i++)
{
for (int j = i + 1; j < _clusters.Count(); j++)
{
clusterPair = new ClusterPair();
clusterPair.Cluster1 = _clusters.GetCluster(i);
clusterPair.Cluster2 = _clusters.GetCluster(j);
yield return clusterPair;
}
}
}
Before we dive into the main method of the Agnes class, it is important to understand how some methods of the DissimilarityMatrix class works. First, let's see the method GetClusterPairDistance.
public double GetClusterPairDistance(ClusterPair clusterPair)
{
double clusterPairDistance = Double.MaxValue;
if (_distanceMatrix.ContainsKey(clusterPair))
clusterPairDistance = _distanceMatrix[clusterPair];
else
clusterPairDistance = _distanceMatrix[new ClusterPair
(clusterPair.Cluster2, clusterPair.Cluster1)];
return clusterPairDistance;
}
The _distanceMatrix is a ConcurrentDictionary and ClusterPair is its key. ClusterPair is formed by two Cluster objects (cluster1 and cluster2) and each Cluster object has it own id. So ClusterPair has two ids, therefore the dictionary has two keys. One of the issues here is that ClusterPair can be formed by cluster1.id = 5 and cluster2.id = 6 OR cluster1.id = 6 and cluster2.id = 5. That why we have the if else statement. The other issue is how to implement a dictionary with two keys? The answer that I found was to override Equals and GetHashCode methods.
public class EqualityComparer : IEqualityComparer<ClusterPair>
{
public bool Equals(ClusterPair x, ClusterPair y)
{
return x._cluster1.Id == y._cluster1.Id &&
x._cluster2.Id == y._cluster2.Id;
}
public int GetHashCode(ClusterPair x)
{
return x._cluster1.Id ^ x._cluster2.Id;
}
}
The GetClosestPair method of the DissimilarityMatrix class is pretty straightforward code, it just looks for the lowest distance value in the matrix. Instead of copying the dictionary values to a List, sorting it and then getting the first value or doing something like that, I preferred using the old fashioned way to find a min value in an unsorted array. I have to be honest with you that my first line of this code was a one line lambda expression ignoring its O(n log n) operation (average case). Of course, there is a better way to do this like to store the min value when adding/deleting the distance value so the min value could be found in constant time O(1), but I just didn't.
public ClusterPair GetClosestClusterPair()
{
double minDistance = double.MaxValue;
ClusterPair closestClusterPair = new ClusterPair();
foreach (var item in _distanceMatrix)
{
if(item.Value < minDistance)
{
minDistance = item.Value;
closestClusterPair = item.Key;
}
}
return closestClusterPair;
}
Now let's have a look at the ComputeDistance method of the ClusterDistance class. The trick part of this method is related to the Average Linkage UPGMA distance. We have to keep track of the total quantity of data points in a cluster (diving into the entire cluster hierarchy) and I had to implement a recursive method to do this (there is another opportunity to improve performance here).
public static double ComputeDistance
(Cluster cluster1, Cluster cluster2,
DissimilarityMatrix dissimilarityMatrix, Strategy strategy)
{
double distance1, distance2, distance = 0;
distance1 = dissimilarityMatrix.GetClusterPairDistance
(new ClusterPair(cluster1, cluster2.GetSubCluster(0)));
distance2 = dissimilarityMatrix.GetClusterPairDistance
(new ClusterPair(cluster1, cluster2.GetSubCluster(1)));
switch (strategy)
{
case Strategy.SingleLinkage: distance = _MinValue(distance1, distance2); break;
case Strategy.CompleteLinkage: distance = _MaxValue(distance1, distance2); break;
case Strategy.AverageLinkageWPGMA: distance = (distance1 + distance2) / 2; break;
case Strategy.AverageLinkageUPGMA:
distance = ((cluster2.GetSubCluster(0).TotalQuantityOfPatterns * distance1) /
cluster2.TotalQuantityOfPatterns) +
((cluster2.GetSubCluster(1).TotalQuantityOfPatterns * distance2) /
cluster2.TotalQuantityOfPatterns);
break;
default: break;
}
return distance;
}
This next method is responsible for updating the dissimilarity matrix as described at the end of the previous section. It is important to make sure that old distance values as well as old clusters (i.e., merged clusters) is removed.
private void _UpdateDissimilarityMatrix
(Cluster newCluster, ClusterDistance.Strategy strategie)
{
double distanceBetweenClusters;
for (int i = 0; i < _clusters.Count(); i++)
{
distanceBetweenClusters = ClusterDistance.ComputeDistance
(_clusters.GetCluster(i), newCluster, _dissimilarityMatrix, strategie);
_dissimilarityMatrix.AddClusterPairAndDistance
(new ClusterPair(newCluster, _clusters.GetCluster(i)), distanceBetweenClusters);
_dissimilarityMatrix.RemoveClusterPair(new ClusterPair
(newCluster.GetSubCluster(0), _clusters.GetCluster(i)));
_dissimilarityMatrix.RemoveClusterPair(new ClusterPair
(newCluster.GetSubCluster(1), _clusters.GetCluster(i)));
}
_dissimilarityMatrix.RemoveClusterPair(new ClusterPair
(newCluster.GetSubCluster(0), newCluster.GetSubCluster(1)));
}
Finally, the BuildHierarchicalClustering recursive method just calls the methods discussed previously and stops when the number of clusters is equals to k (i.e., user-defined number of clusters).
private void BuildHierarchicalClustering
(int indexNewCluster, ClusterDistance.Strategy strategy, int k)
{
ClusterPair closestClusterPair = this._GetClosestClusterPairInDissimilarityMatrix();
Cluster newCluster = new Cluster();
newCluster.AddSubCluster(closestClusterPair.Cluster1);
newCluster.AddSubCluster(closestClusterPair.Cluster2);
newCluster.Id = indexNewCluster;
newCluster.UpdateTotalQuantityOfPatterns();
_clusters.RemoveClusterPair(closestClusterPair);
_UpdateDissimilarityMatrix(newCluster, strategy);
_clusters.AddCluster(newCluster);
closestClusterPair = null;
if (_clusters.Count() > k)
this.BuildHierarchicalClustering(indexNewCluster + 1, strategy, k);
}
Actually, before AggloCluster outputs the clustering results as displayed in Figures 3 and 4, one more step needs to be done; it is necessary to transform the hierarchical clustering structure (AGNES is a hierarchical clustering algorithm) into flat clusters with k partitions.
public Cluster[] BuildFlatClustersFromHierarchicalClustering(Clusters clusters, int k)
{
Cluster[] flatClusters = new Cluster[k];
for (int i = 0; i < k; i++)
{
flatClusters[i] = new Cluster();
flatClusters[i].Id = i;
foreach (Pattern pattern in clusters.GetCluster(i).GetAllPatterns())
flatClusters[i].AddPattern(pattern);
}
return flatClusters;
}
Points of Interest
Machine learning is a very interesting subject to learn, however, it can be difficult to understand if you don't have a strong background in math/statistics. So to overcome this, I found a way to understand many of the fancy math notations and concepts described in pattern recognition books by doing some code and translating into a language that I could understand. As a result, I can say that I have a more intuitive idea on how some unsupervised machine learning algorithms work and I hope, after reading this article, you can have that same intuition too.
If you got interested in the SharpCluster.NET/AggloCluster project, please feel free to join me on Github. There is a lot of work to do there from improving the algorithm's performance to building a more friendly UI.
