Implementing a memory efficient search tree for a wordlist

Summary

This article describes a method of storing a wordlist (all the words listed in a dictionary, but without their definitions) into a compressed form while providing a relatively quick word lookup functionality.

Motivation and background

At some point in time, I was implementing a word game on an embedded platform that required players to create valid words out of letters for whom they would get points. The way the game was going required couple of word lookups every second. It was necessary to have some kind of dictionary for validating the words, and we had both size and speed limitations.

The wordlist we started with (and we changed a little later) was about 1 MB in size. While on modern computers that would seem very small, on an embedded platform (as in our case) that was quite a lot.

Few details about the platform we were using: the available memory was a little less than 8 MB, the CPU was not very fast, and moreover it had to take care of a lot of other tasks (graphics, sound and more); all that meaning the lookup routine had to be quite fast. No multilingual support was needed as the game only had an English version.

At the application level, the platform was running a virtual machine that was based on LUA. The LUA language has the concept of tables, which can be used as associative arrays (internally implemented using hash tables), and that seemed at the time as a very appropriate way to implement the wordlist. Using the LUA tables, with the words as key, the lookup function would be really simple, something like:

function Lookup(w)
    if wordlist[w] == nil then 
        return false
    end

    return true;
end

Preliminary tests with a reduced wordlist showed that the lookup speed was indeed fast, and the byte-code representation of the table was about the 1.5 to two times bigger than the size of the wordlist itself.

However, when the almost complete wordlist was used and the program was running, it showed up that a 1 MB table would eat up about 8 MB of memory, that being actually almost the whole memory the system had available. Clearly, there was a problem, and some solution had to be found.

First, some understanding of where the memory was going was required. After some research, it became clear that the problem was because of the memory allocator used by the system and also because of the actual way the tables were implemented in LUA.

First, the memory allocator, was rounding up each allocated block to a size multiple of 4 and it was using two extra pointers internally to manage the memory block (that would be another 8 bytes). So a four letter word would end up using 16 bytes (4 bytes for the letters, 1 byte for the terminating null character, 3 bytes for padding and 8 bytes to hold the allocator's internal pointers). That alone would grow up the memory usage about 4 times in average.

Second, the VM table implementation was done using hash tables, and hash tables inherently waste memory, which in combination with the memory allocator problem resulted in the practical impossibility of using this approach in our situation.

At that time, a decision (primarily due to linguistic reasons) was made to reduce the wordlist, and the new wordlist went to about 600 KB in size – however the problem with the memory usage still remained as the game needed most of the memory of the system to store graphic textures.

The first idea was to put all words each after another in the memory and do a linear search through the list that somehow solved the memory problem but completely ignored the speed aspect of the problem. The search speed was of course horrible, so I started splitting up the list first in 26 lists, each of them containing words starting with the same letter. While that definitely speed up the search, it was still slow, so I started adding a second index, for the second letter in the word, now having 26*26 = 676 tables. That added another speedup, but was still not enough. Soon I realized that a lot of words have a common prefix, or even more, sometimes they only have just 1 or two letters different at the end (words like buzz, buzzed, buzzer, buzzers, buzzes, buzzing). That made me think that a tree structure would be more appropriate for me, so I started implementing one.

A first implementation (search tree)

Consider the following words : abc, abd, abcd, abcde, abcdf, abcdfa, abcdfb, abcdfc.

They can be represented as a tree in the following manner:

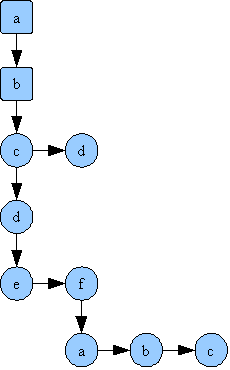
When traversing the tree from root downwards, and selecting only one letter per level, words will be formed, and the round characters will mark the end of a valid word.

Notice that the common suffix (abc for example) is actually stored only once, and it's reused for all the words that it forms.

The tree can be implemented (in C++) this way:

struct Node
{
    char ch;
    bool b_fullword;
    Node * next;
    Node * down;
};

To add a word to the tree we'll do something like:

Node * d = root;
char * s = lookup_word;
while (! b_done)
{
    // look horizontally
    while ( ( d->ch != *s ) && (d->next != NULL) )
    {
        d = d->next;
    };
    
    // we verify if we found the letter
    if ( d->ch != *s )
    {
        // letter not found, we start adding it
        d->next = CreateNode();
        d->next->ch = *s;
        d = d->next;
        s++;
        AddDown(d, s);
        b_done = 1;
    }
    else
    {
        // letter found, go to next letter
        s++;

        if (*s == 0)
        {
            // it was the last letter
            d->b_fullword = 1;
            b_done = 1;
        }
        else
        {
            // there are still letters in the word
            if (d->down)
            {
                d = d->down;
            }
            else
            {
                AddDown(d, s);
                b_done = 1;
            }
        }
    }
}

The AddDown function looks like this:

while (*s != 0)
{
    d->down = CreateNode();
    d->down->ch = *s;
    s++;
    d = d->down;
}
d->b_fullword = 1;

The lookup function will start from the root and look horizontally for the current letter. Once it finds it, it goes down and repeats the procedure, until the string ends, or it cannot find a letter anymore or there is no down link anymore. The routine will have to check if the last node visited terminates a word (b_fullword is true) before returning success.

An analysis of the complexity

Obviously, the search speed will depend on the number of letters in the alphabet and the length of the lookup word. The first is constant, and the second is also limited (in our case we limited the words to 8 letters, but generally speaking the words will have a small limited number of letters). The worst theoretical situation was to traverse 26 nodes 8 times, that being 208 nodes, but on an average a lookup would only do 20 to 40 node traversals, which was reasonable in our case.

The memory requirements however turned out to be quite high. The wordlist we used generated about 150,000 nodes, each of them using 12 bytes of memory (bool type was using 4 bytes on that machine, and the structure was rounded up to 4-byte boundary), and the allocator eating up another 8 bytes for each node we were actually using about 3 MB of memory.

Luckily, the structure is yet far from being optimized, as we can actually reduce the memory usage without penalizing the search speed.

A second implementation (serialized search tree)

The first thing we can do is to actually remove the overhead of the memory allocator, which eats up 8 bytes for each node (our case, some other allocators might use more or less) that represents little less than half of the memory used by the node.

To do this we have to lay out the nodes consecutively in memory, in a preallocated memory chunk, and have the pointers to next and down elements reflect the new node memory position.

Implementation details for doing this are beyond the scope of the article, as there is nothing special about it.

However, memory-wise, we now have 150 K nodes of only 12 bytes now that eats up only 1.8 MB of memory.

A better implementation (serialized search tree, grouped and packed letters)

A quick look over the implementation, and we realize that we waste 4 byes (sizeof (Node*)) for each node in order to hold a pointer to the next horizontal letter, where we could actually have an array of nodes forming a chunk of letter nodes, each of the nodes only having a letter, a full word flag and the down pointer.

Also, the English alphabet uses only 26 letters, and for our scope we did not differentiate between uppercase and lowercase, so we actually needed only 5 bits to store the letters, and 1 bit to store the full word flag, so we can combine them into one byte.

A node would now have 1 byte containing the letter and the flag, and 4 bytes for the down pointer and all the letters on the same level that continue a prefix would be grouped into chunks. The chunks will start with 1 byte that holds the number of letters in the chunk followed by 5 bytes for each letter. For now we'll consider that a node is taking up 5 bytes (it would be taking a maximum of 6 bytes, and on an average something in between), so we are now using 150 K * 5 bytes = 750 KB of memory!

That is way better than what we originally started with, but we can do even better.

An even better implementation (packed letters and variable length pointers)

Now we use 5 bytes to store a letter in the tree, 1 byte for the letter and the flag, and 4 bytes for the down pointer. But do we really need 4 bytes to store the pointer? If we use a relative pointer to the start of the memory block we would only need 20 bits to represent the distance (20 bits will address 1 MB of memory).

We could use only 3 bytes for the pointers, and gain some more memory. However, depending on the arrangement of the nodes in the memory, we might actually need less addressing bits for the pointer.

Remember we have 2 bits left in the letter+flag byte ? We could use them to actually store the size of the down pointer. Let's call them psize bits for now.

For a node that has no down pointer we'll set psize = 0.

• If the relative position of the next node fits in one byte we'll set psize = 1.
• If the relative position of the next node fits in two bytes we'll set psize = 2.
• If the relative position of the next node fits in three bytes we'll set psize = 3.
• If the relative position of the next node does not fit in three bytes we'll just abort the process (in the case of our wordlist that is impossible).

Now of course the order we lay out the nodes into the memory chunk will affect the relative distances between them. In the general case, we can try to find the optimal arrangement of nodes that will minimize the pointer size, but I am not aware of any fast (practical) algorithm that will do that.

One way would be brute force – generate all possible arrangements and try them all, this way we'll find for sure the optimum. Another way would be using some Monte Carlo methods – try out random permutations until the results seem to approach an optimum. While I did not actually try it, this approach might actually provide some results.

Another more practical way is to lay out the nodes in the memory in a "natural" order. To achieve that, we'll have to keep in mind the data we put in – words. In a ordered wordlist, most words will have a common prefix with the next word, so if we'd be putting all the suffixes close to each other in the tree, the pointers to each other will be relatively short. An easy way of doing that is to traverse the tree from the root downwards, adding a node then visiting its down descendants, from left to right.

In our case, traversing the tree that way leads to the following results:

• psize == 0 : 56131 elements
• psize == 1 : 91064 elements
• psize == 2 : 6696 elements
• psize == 3 : 28 elements

Now we use 1 byte for elements with psize == 0, 2 bytes for psize == 1 and so on.

Only about 5 % of the elements use 3 or 4 byes of memory, about 58 % use 2 bytes and about 36 % use 1 byte.

Now the memory usage of the wordlist has dropped down to 345 KB, which is almost 10 times smaller than the memory used by the original tree, while we still can do quick word lookups!

Conclusion

We have shown above how we managed to compress the word list size while still providing a relatively fast lookup routine. There are other possible improvements that can speed up the search and still reduce the memory, and we'll present a few of them below:

1. The root node of the tree and the level 2 nodes will likely contain most of the letters of the alphabet. It might be worth for those nodes to have a special node structure, where we can allocate 4 bytes for each letter of the alphabet, 3 bytes for storing the down pointer and one byte for storing the full word flag and a flag to determine if the letter actually exists. Looking up a letter in that node will be done in constant time (as it's just an index in the array). This will increase a little the size of the wordlist, but it would speed up the search a lot.
2. Most of the nodes in the tree (more than 50%) only have a letter, and they use 2 bytes + psize to represent it. A special case for that situation would save up a lot of memory. A way to do this can be adding a flag in the down pointer (that would of course increase the down pointer size, but on an average there will still be a significant memory gain).
3. The size of the wordlist can now be fully addressed with a 19 bit pointer, but we sometimes use 24 bits. Changing the data structures so that they use half-bytes instead of full bytes (and further more bit-packing the nodes) may gain some additional memory. However, that approach will have to overcome some other issues (pointer size will now require 3 bits, and it will not fit into two 2 half-byte "memory cells"; memory address space will double requiring one extra address bit; search would be slowed down by the extra bit-unpacking requirements).

However the reason somebody needs to use a wordlist, organizing it into this kind of structure will save some memory and speed up the search. Even on a modern machine, having a small-memory-usage wordlist would be more cache-friendly, thus the performance of the application will be better.