Java based Quantum Computing library

Introduction

“Anyone who is not shocked by quantum theory has not understood it.” Niels Bohr.

A quantum computer differs from traditional one by making use of quantum mechanical effects, such as superposition, to carry out computations. In a traditional computer, the basic unit is represented by a bit which has either value 0 or 1. In comparison to a traditional computer, the basic unit for a quantum computer is the qubit which can at one time represent the value 0 and 1, by exploiting superposition.

In this article I would like to present a Java library that allow to simulate quantum algorithms. I wrote this library because I saw that there is a lack of Java based libraries that simulate quantum algorithms, the existing Java based simulators don’t export the API and they can’t be used in projects. 

Background

Since quantum computing might not be a well-known topic to the readers, I will make a short introduction to the subject before I will start presenting algorithms implemented using the library. In this chapter I will talk about complex numbers, vectors and qubits.

 

Complex Numbers

Because probability amplitudes of a qubit are complex numbers, I will start with a short introduction in the mathematics behind complex numbers and after that I will present the most basic operations.

A complex number q is defined as

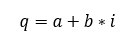
where a and b are real numbers and 

is the imaginary basis unit. It can be easily see that a complex number has a real component “a” and an imaginary one, “b*i”. By negating the sign of the imaginary component of a complex number the complex conjugate is obtained.

Now, about the basic operations, I will present the formulas beyond addition, multiplication, modulus and complex conjugate.

If we consider 2 complex numbers x and y,

The addition of these 2 numbers is defined as:

The multiplication is defined by:

is the modulus of the complex number x and the complex conjugate is defined as:

Vectors

In this subchapter I will make a short introduction in vectors and linear algebra. Formally, the state of a qubit is a unit vector in a 2-dimensional complex vector space C².

The vector can be written aswhere 

This notation of a column vector is called ket. The corresponding row vector is called bra.

The inner product <v|v> is the bra-ket or dot product between the bra and the ket vectors:

The outer product is the ket-bra and is given by:

The tensor product is defined in this way. If then the tensor product is:

Qubits and Gates

Quantum mechanics tells us that any such system can exist in a superposition of states. In general, the state of a qubit is described by: where a and b are complex numbers satisfying 

On a classic computer gate operations such as AND and OR constitute the core of data manipulation, on a quantum computer similar operations are possible on qubits.  The gate operations possible to perform are exactly all unitary linear operations.

An important example is the Hadamard transformation. This is defined as

Or if we consider  it can be represented as the matrix:

A Hadamard gate creates a superposition state, often beginning a quantum computation to initiate data processing and then ending a quantum computation to collect data.

A particularly useful set of 1-qubit gates are the Pauli Gates, the X gate, Y gate and Z gate.

 

Using the code

In this chapter I will make a brief description of the Quantum Computing Library and I will present the implementation of the Deutsch's Algorithm.

Brief description of the library

The Quantum Computing library contains definitions of the well-known gates and basic qubits. Also, it contains implementations of the needed matrix and vectors operations.

The class Qubit is used to create new Qubit object and it contains methods for testing if a qubit is valid or for testing if two qubits are equal. Class Qubit is inherited by subclasses that defines the "basic" qubits |0>, |1>, |+> and |->.

/**
	 * Constructs a new <code>Qubit</code> object. 
	 * @param no0 complex number
	 * @param no1 complex number
	 * 
	 */
	public Qubit(ComplexNumber no0, ComplexNumber no1) {
		qubitVector = new ComplexNumber[2];
		qubitVector[0] = no0;
		qubitVector[1] = no1;
	}

	/**
	 * Constructs a new <code>Qubit</code> object.
	 * @param qubitVector an array of 2 complex numbers
	 */
	public Qubit(ComplexNumber[] qubitVector) {
		this.qubitVector =Arrays.copyOf(qubitVector, qubitVector.length);
	}

	/**
	 * Return the qubit represented as an array of 2 complex numbers.  
	 * @return qubit
	 */
	public ComplexNumber[] getQubit() {
		ComplexNumber[] copyOfQubitVector = qubitVector;
		return copyOfQubitVector;
	}

/**
 * Check if qubit state is valid
 * @return true if the state is valid, otherwise false
 */
public boolean isValid(){
    double sum=0.0;
    for(ComplexNumber c:this.qubitVector){
        double mod=ComplexMath.mod(c);
        sum+=mod*mod;
    }
    return (sum==1.0);
}

QubitOne |1> and QubitZero |0> classes are defined below:

public class QubitOne extends Qubit {

	/**
	 * Construct a new <code> QubitOne</code> object.
	 */
	public QubitOne() {
		super(new ComplexNumber(0.0, 0.0), new ComplexNumber(1.0, 0.0));
	}

}

public class QubitZero extends Qubit {

	/**
	 * Construct a new <code> QubitZero</code> object.
	 */
	public QubitZero() {
		super(new ComplexNumber(1.0, 0.0), new ComplexNumber(0.0, 0.0));
	}

}

Gates are implemented in the library using the abstract factory pattern and for creating a new Gate object is needed to add the following lines:

GatesAbstractFactory gateFactory = GateProducer.getGateFactory();
gateH = gateFactory.getGate(EGateTypes.E_HadamardGate);

For now, the only implemented gates are:

• Hadamard Gate
• Pauli's Z-Gate
• Pauli's X-Gate
• C-Not Gate

/**
 * Implemented Quantum Gates.
 * 
 *
 */
public enum EGateTypes {
	/**
	 * Hadamard Gate
	 */
	E_HadamardGate,
	/**
	 * Pauli-X Gate
	 */
	E_XGate,
	/**
	 * Pauli-Z Gate
	 */
	E_ZGate,
	/**
	 * CNOT Gate
	 */
	E_CNotGate
}

 

Deutsch's Algorithm

Instead of describing each line of code from the Quantum Computing library I preferred to show an implementation of a well-known and simple quantum algorithms. In the project's repository there is also the implementation of Grover's algorithm and in future I will add Deutsch-Josza and Shor's algorithms. 

The problem that Deutsch’s algorithm solves is not an important problem in Computer Science but is a good problem to see how quantum computers can be used. This problem can be solved by a quantum computer faster than a traditional one, although not exponentially faster.

Let’s suppose there is a function f which has 1-bit inputs/outputs 

and we are asked if this function is constant or balanced. The maximum number of such function is 4:

The quantum circuit of the Deutsch's Algorithm look the following way:

So the steps that we need to implement this simple algorithm are:

• Initialization
  • Create |0> (QubitZero) object;
  • Create X-Gate and H-Gate Objects
  • Perform the tensor product between the matrices that defines the Hadamard Gate;
• Algorithm
  • Apply X-Gate to the second qubit 0. Let's call the resulted qubit result
  • Entangle |0> and result qubits
  • Apply Hadamard Gate
  • Apply Oracle
• Measurement

//Initialization
gateH = gateFactory.getGate(EGateTypes.E_HadamardGate);
		gateX = gateFactory.getGate(EGateTypes.E_XGate);
		gateHH = MatrixOperations.tensorProduct(gateH.getUnitaryMatrix(), gateH.getUnitaryMatrix());

//Running the algorithm
resultQubit = QuantumOperations.applyGate(QuantumOperations.applyGate(
				QuantumOperations.applyGate(
						QuantumOperations.entangle(QUBIT_0, QuantumOperations.applyGate(QUBIT_0, gateX)), gateHH),
				oracle), gateHH);

//Measurement
measurementResults = new double[resultQubit.getQubit().length];
int i = 0;
for (ComplexNumber c : resultQubit.getQubit()) {
	measurementResults[i++] = Math.round(ComplexMath.multiply(c, ComplexMath.conjugate(c)).getReal());
}

//Helping method to test if a function is constant or not
public boolean isFunctionConstant() {
		int i = 0;
		ComplexNumber[] q01 = QuantumOperations.entangle(QUBIT_0, QUBIT_1).getQubit();
		for (ComplexNumber c : q01) {
			if (Double.compare(Math.round(ComplexMath.multiply(c, ComplexMath.conjugate(c)).getReal()),
					measurementResults[i++]) != 0) {
				return false;
			}
		}
		return true;

	}

 

Points of Interest

About this project I only can say that it bought me a lot of fun and also I learned a lot. Also, like any new thing, it also bought me some frustration but it was interesting. I found Quantum Computing subject interesting, I start to read courses and articles about it and I understood the math and the “magic” behind and writing the library was a good exercise and I needed to apply all the new knowledge.

About future improves to this library, I would have to implement a system to better treat exceptions and also I plan to use C++ and JNI to gain a performance improvement.

 

The repository of this project can be found HERE.

 

History

•  Article added
• updated quotation
• added link to repository