Introduction
In a previous article I talked about a Quantum Computing Library that I wrote and I presented, as an example, the implementation of Deutsch's Algorithm. In this article I will present the Grover's Search algorithm.
The algorithm formulated by Lov Grover in 1996 uses a feature of quantum interference in order to solve an extremely demanding task of searching the value of some parameter, at which a defined function returns certain results, over an unordered set of \(N=2^{n}\). The algorithm performs a search on a quantum computer in only \(O(\sqrt{N})\) operations, while the best classical algorithm for a search over unordered data requires O(N) time.
Background
Grover's algorithm begins with a quantum register of n qubits, where n is the number of qubits necessary to represent the search space of \(2^{n}=N\), all initialized to \(|0\rangle\):
$\begin{equation} |0^{\otimes n}\rangle=|0\rangle \end{equation} $
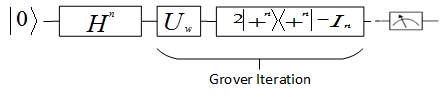
The first step is to put the system into an equal superposition of states, achieved by applying the Hadamard transform \(H^{\otimes n}\):
$ \begin{equation} |\psi\rangle=H^{\otimes n}|0^{\otimes n}\rangle=\frac{1}{\sqrt{2^{n}}}\displaystyle\sum_{x=0}^{2^{n}-1}|x\rangle \end{equation} $
The next series of transformations is often referred to as the Grover Iteration and it will be repeated \(\frac{\pi}{4}{\sqrt{2^{n}}}\) times. A call to a quantum oracle O, a quantum black-box that can observe and modify the system without collapsing it to a classical state, represents the first step in the Grover iteration.
$ \begin{equation} |x\rangle\xrightarrow{O}(-1)^{f(x)}|x\rangle \end{equation} $
where \(f(x)=1\) if x is the correct state, and 0 otherwise.
The next part of the iteration is referred as the diffusion transform which performs inversion about the average, transforming the amplitude of each state. The diffusion transform consist of another application of the Hadamard transform \(H^{\otimes n}\), followed by a conditional phase shift that shifts every state except \(|0\rangle\) by -1, follower by another Hadamard transform.
The conditional phase shift can be represented by the unitary operator
$ \begin{equation} 2|0^{\otimes n}\rangle\langle 0^{\otimes n}|-I \end{equation} $
Given the entire diffusion transform, using the notation \(\psi\) from equation 2:
$ \begin{equation} H^{\otimes n}[2|0^{\otimes n}\rangle\langle 0^{\otimes n}|-I]H^{\otimes n}= 2H^{\otimes n}|0^{\otimes n}\rangle\langle 0^{\otimes n}|H^{\otimes n}-I= 2|\psi^{\otimes n}\rangle\langle\psi^{\otimes n}|-I \end{equation} $
And the entire Grover iteration:
$ \begin{equation} [2|\psi^{\otimes n}\rangle\langle\psi^{\otimes n}|-I]O \end{equation} $
Example
Let's assume that there's a binary function from n binary arguments, which accepts the value of 1 at one of them only. It is required to find the value of input arguments for which f(x)=1.
So, let's consider the following task:
$ \begin{equation} f(x_1,x_2,x_3)=x_1\&x_2\&x_3 \end{equation} $
. This function accepts value of 1 only in one of the eight variants of input values, more exactly when
$ \begin{equation} x_1=x_2=x_3=1\Rightarrow f(x_1,x_2,x_3)=1 \end{equation} $

Algorithm's Steps
- Initial state \(|0^{\otimes n}\rangle\)
- Apply the Hadamard transform to all qubits:\(H^{\otimes n}|0^{\otimes n}\rangle\)
- Apply the Grover iteration 3 times
- Measure the register
Results
The following 8x8 matrix correspond to the table:
$ O= \begin{pmatrix} 1&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&-1 \end{pmatrix} $
Now that we have the oracle, let's calculate the diffusion matrix:
$ D=2|+^{\otimes n}\rangle\langle +^{\otimes n}|-I_n $
Finally, if we will apply the Grover iteration 3 times we will obtain:
$ |\psi\rangle= \begin{bmatrix} -0.309359 \\ -0.309359 \\ -0.309359 \\ -0.309359 \\ -0.309359 \\ -0.309359 \\ -0.309359 \\ 0.574524 \end{bmatrix} $
Using the code
First of all, before starting implementing the steps from Grover's algorithm, we will define a method for creating the diffusion matrix:
private void generateDiffusionMatrix() {
diffusionMatrix = QuantumOperations.outerProduct(qubitPlus, qubitPlus);
diffusionMatrix = MatrixOperations.multiplyByConstant(diffusionMatrix, 2);
ComplexNumber[][] identityMatrix = MatrixOperations.generateIdentityMatrix(8);
diffusionMatrix = MatrixOperations.subtract(diffusionMatrix, identityMatrix);
}
The implementation will have 3 public methods:
- init()- will create the Hadamard Gate object, Qubit objects and set the initial state;
- run()- will perform the Grover iteration 3 times;
- measure()- will perform the measurement
@Override
public void init() {
gateH = gateFactory.getGate(EGateTypes.E_HadamardGate);
resultQubit = QUBIT_0;
qubitPlus = new QubitPlus();
for (int i = 0; i < NO_OF_INPUT - 1; i++) {
resultQubit = QuantumOperations.entangle(resultQubit, QUBIT_0);
}
for (int i = 0; i < NO_OF_INPUT - 1; i++) {
qubitPlus = QuantumOperations.entangle(qubitPlus, new QubitPlus());
}
gateHn = gateH.getUnitaryMatrix();
for (int i = 0; i < NO_OF_INPUT - 1; i++) {
gateHn = MatrixOperations.tensorProduct(gateHn, gateH.getUnitaryMatrix());
}
setOracle(oracleMatrix);
generateDiffusionMatrix();
}
@Override
public void run() {
int noOfIterations = (int) Math.sqrt(Math.pow(2, NO_OF_INPUT));
resultQubit = QuantumOperations.applyGate(resultQubit, gateHn);
for (int i = 0; i < noOfIterations + 1; i++) {
resultQubit = QuantumOperations.applyGate(resultQubit, oracleMatrix);
resultQubit = QuantumOperations.applyGate(resultQubit, diffusionMatrix);
}
assert (resultQubit.isValid() == true);
}
@Override
public void measure() {
MeasurementPerformer measurementPerformer = new MeasurementPerformer().configure(resultQubit);
resultQubit = measurementPerformer.measure();
}
After running Grover's Algorithm 1 million times, the next chart is obtained:

We can observe that the correct answer |111> was obtained in almost 350000 of 1 million runs.
Points of Interest
I found interesting to simulate well-known quantum algorithms using my implementation of a Quantum Computing library. In this way I can add more features to it and also find some small bugs. Also, I think is a good way to understand Quantum Algorithms.
Bibliography
An Introduction to Quantum Algorithms,Emma Strubell,Spring 2011
Qubits, Quantum Mechanics and Computers, Umesh V. Vazirani, Spring 2005
History
- Added article
- Added license GPL3
