Implementation of Gauss–Newton Algorithm in Java

• Download source code - 9.6 KB

Introduction

Gauss-Newton algorithm is a mathematical model to solve non-linear functions. A simple non-linear function is given below:

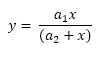
where a₁ and a₂ are the unknown parameters of this function. To find these two parameters, the values of y are measured on different values of x; y can be the rate of a chemical reaction and x is the concentration of a chemical affecting the rate. The results may look like this:

x	0.038	0.194	0.425	0.626	1.253	2.500	3.740
y	0.050	0.127	0.094	0.2122	0.2729	0.2665	0.3317

Gauss-Newton algorithm is used to estimate the values of a₁ and a₂ using the observed data above.

This sample function and the data are taken from https://en.wikipedia.org/wiki/Gauss-Newton_algorithm.

Background

Gauss-Newton algorithm in a few steps:

1. Create an array of unknown parameters in the function:

   b = (b₁, b₂,...,b_n)

2. Initialise the parameters and for each data point in matrix x, calculate the predicted values (y').
3. Calculate the residuals:

   r_i = y'_i - y_i

4. Find the partial differential of residuals with respect to the parameters and generate Jacobian matrix.

   

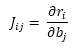
5. Following an iterative process, calculate the new values for the parameters using the following equation:

   

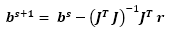
   s is the iteration number, J is the Jacobian matrix, J^T is the transpose of J.

For more information, please visit https://en.wikipedia.org/wiki/Gauss-Newton_algorithm.

Using the Code

In this implementation, I will be using some matrix operations that have already been implemented in another article. For more information, please take a look at this article.

1. Given matrix x and y, the optimization starts with an initial guess of b matrix. By default, a value of 1.0 is given to all parameters in non-linear function.
2. Calculate the residuals:
   Java

   public double[][] calculateResiduals(double[][] x, double[] y, double[] b) {
        double[][] res = new double[y.length][1];
   
        for (int i = 0; i < res.length; i++) {
            res[i][0] = findY(x[i][0], b) - y[i];
        }
        return res;
   }

   For each data point in x matrix, function findY() is called to calculate the predicted value of y. In the code, you will find this function as abstract:

   Java

   public abstract double findY(double x, double[] b);

   The user needs to implement this function before using the optimization. For example, for the function in the introduction, the implementation will be as follows:

   Java

   GaussNewton gaussNewton = new GaussNewton() {
   
       @Override
       public double findY(double x, double[] b) {
           // y = (x * a1) / (a2 + x)
           return (x * b[0]) / (b[1] + x);
       }
   };
   

3. Calculate the Jacobian matrix which is the partial derivatives of the residuals with respect to parameters in the function:
   Java

   public double[][] jacob(double[] b, double[][] x, int numberOfObservations) {
       int numberOfVariables = b.length;
       double[][] jc = new double[numberOfObservations][numberOfVariables];
   
       for (int i = 0; i < numberOfObservations; i++) {
           for (int j = 0; j < numberOfVariables; j++) {
               jc[i][j] = derivative(x[i][0], b, j);
           }
       }
       return jc;
   }
   

   Function derivative() is called to calculate the partial derivative:

   Java

   public double derivative(double x, double[] b, int bIndex) {
       double[] bCopy = b.clone();
       bCopy[bIndex] += alpha;
       double y1 = findY(x, bCopy);
       bCopy = b.clone();
       bCopy[bIndex] -= alpha;
       double y2 = findY(x, bCopy);
       return (y1 - y2) / (2 * alpha);
   }
   

   This function gives a good approximate of the partial derivative; i.e., the change in y after a small change in the variable.

4. Perform (J J^T)^-1 J^T r operations:
   Java

   public double[][] transjacob(double[][] JArray, double[][] res) throws NoSquareException {
       Matrix r = new Matrix(res); // r
       Matrix J = new Matrix(JArray); // J
       Matrix JT = MatrixMathematics.transpose(J); // JT
       Matrix JTJ = MatrixMathematics.multiply(JT, J); // JT * J
       Matrix JTJ_1 = MatrixMathematics.inverse(JTJ); // (JT * J)^-1
       Matrix JTJ_1JT = MatrixMathematics.multiply(JTJ_1, JT); // (JT * J)^-1 * JT
       Matrix JTJ_1JTr = MatrixMathematics.multiply(JTJ_1JT, r); // (JT * J)^-1 * JT * r
       return JTJ_1JTr.getValues();
   }
   

5. Using the results of step 4, the new values of the parameters are calculated:
   Java

   IntStream.range(0, values.length).forEach(j -> b2[j] = b2[j] - gamma * values[j][0]);

   b₂ is the new b matrix. gamma is a fraction of the values coming from Jacobian. If the initial values for b are far from optimum, there is a possibility of convergence problem. Applying this simple fraction seems to solve this issue. The downside of applying this fraction is the number of iterations which will increase.

6. Having the new b matrix, repeat steps 2-5 in the next iteration. All optimisation steps are given in the function below:
   Java

   public double[] optimise(double[][] x, double[] y, double[] b) throws NoSquareException {
           int maxIteration = 1000;
           double oldError = 100;
           double precision = 1e-6;
           double[] b2 = b.clone();
           double gamma = .01;
           for (int i = 0; i < maxIteration; i++) {
               double[][] res = calculateResiduals(x, y, b2);
               double error = calculateError(res);
               System.out.println("Iteration : " + i + ", Error-diff: " + 
                       (Math.abs(oldError - error)) + ", b = "+ Arrays.toString(b2));
               if (Math.abs(oldError - error) <= precision) {
                   break;
               } 
               oldError = error;
               double[][] jacobs = jacob(b2, x, y.length);
               double[][] values = transjacob(jacobs, res);
               IntStream.range(0, values.length).forEach(j -> b2[j] = b2[j] - gamma * values[j][0]);
           }
           return b2;
   
       }

Example

Function

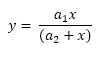
Observations

x	0.038	0.194	0.425	0.626	1.253	2.500	3.740
y	0.050	0.127	0.094	0.2122	0.2729	0.2665	0.3317

Target

Find a₁ and a₂ using the above data and Gauss-Newton algorithm:

@Test
public void optimiseWithInitialValueOf1() throws NoSquareException {
    double[][] x = new double[7][1];
    x[0][0] = 0.038;
    x[1][0] = 0.194;
    x[2][0] = 0.425;
    x[3][0] = 0.626;
    x[4][0] = 1.253;
    x[5][0] = 2.500;
    x[6][0] = 3.740;
    double[] y = new double[] { 0.050, 0.127, 0.094, 0.2122, 0.2729, 0.2665, 0.3317 };
    GaussNewton gaussNewton = new GaussNewton() {

        @Override
        public double findY(double x, double[] b) {
            // y = (x * a1) / (a2 + x)
            return (x * b[0]) / (b[1] + x);
        }
    };
    double[] b = gaussNewton.optimise(x, y, 2);
    Assert.assertArrayEquals(new double[]{0.36, 0.56}, b, 0.01);
}

In the above test, the initial values for the parameters are the default value (1.0); however, with starting values of 100, we will get the same values; see the attached codes. I have also tested the algorithm on a large set of randomly generated data and it works with good time and memory efficiency; see the test codes attached.

History

This is the first version of this article.