Get the latest source on GitHub: https://github.com/cliftonm/MerkleTree
Contents
In 1979, Ralph Merkle1 patented3 the concept of hash trees, or better known as a Merkle tree (the patent expired in 2002.) In summary: "The invention comprises a method of providing a digital signature for purposes of authentication of a message, which utilizes an authentication tree function of a one-way function of a secret number."
Or, if you prefer Wikipedia's definition: "In cryptography and computer science, a hash tree or Merkle tree is a tree in which every non-leaf node is labeled with the hash of the labels or values (in case of leaves) of its child nodes. Hash trees allow efficient and secure verification of the contents of large data structures. Hash trees are a generalization of hash lists and hash chains."2
I'll attempt to use a consistent terminology throughout this article, except where directly quoting some reference material.
Record - a boring word that describes a packet of data whose hash corresponds to a "leaf" in a Merkle tree. When reading about Merkle trees, you'll see other words like "transaction" or "certificate" depending on the context.
Block - borrowing from bitcoin, I'm going to use the term "block" to mean all the permanent records that represent the leaves of the Merkle tree. To quote bitcoin: "Transaction data is permanently recorded in files called blocks. They can be thought of as the individual pages of a city recorder's recordbook (where changes to title to real estate are recorded) or a stock transaction ledger."8 In other words: "records are permanently recorded in files called blocks."
Log - synonymous for the Merkle tree, a log is the hash tree constructed from the hashed records. In addition to the log being represented as a hash tree, the log has a specific property: new entries are always appended as a new leaf (or leaves) to the last leaf in the tree. Furthermore, for transactional systems (like currencies), once a record is "logged", it cannot be changed--instead, changes to the transaction are represented as new record entries in the log, providing a complete audit trail of a transaction. Conversely, a distributed datastore (like a NoSQL database) where a record is allowed to change will update the hash of the record and thus the entire tree. In this scenario, a Merkle tree is used to quickly and efficiently identify the changed record so that nodes in the distributed system can be synchronized.
Merkle trees (and variations) are used by Bitcoin4, Ethereum6, Apache Cassandra5, and other systems to provide:
- consistency verification
- data verification
- data synchronization (you'll have to wait for Part II, because data synchronization is a whole article unto itself.)
What do these terms mean? I'll explain that soon!
The concept of blockchains, which leverages Merkle trees, is growing in popularity beyond bitcoin. Businesses that need to track data and verify the integrity of the data are beginning to see how blockchains assist in that process.
For example, IBM and Laersk are teaming up to use blockchains for managing the global supply chain:
"Technology giant IBM (NYSE: IBM) and Maersk, owner of the leading transport and logistics company Maersk Line, have announced a potentially groundbreaking collaboration to use �blockchain� technology to digitize transactions among the world�s vast and interconnected network of shippers, freight forwarders, ocean carriers, ports and customs authorities participating in the supply chain.
If widely adopted, the technology could transform the global, cross-border supply chain and save the industry billions of dollars, according to IBM and Maersk."10
"Google�s AI-powered health tech subsidiary, DeepMind Health, is planning to use a new technology loosely based on bitcoin to let hospitals, the NHS and eventually even patients track what happens to personal data in real-time.
Dubbed �Verifiable Data Audit�, the plan is to create a special digital ledger that automatically records every interaction with patient data in a cryptographically verifiable manner. This means any changes to, or access of, the data would be visible."11
Don't spend 2,500 British Pounds to read the study. And should you ask, no, I didn't either.
"Despite the fact that the blockchain was initially developed as a freely-accessible, utility-like alternative to traditional means of recording and storing the transfer of assets between counterparties within a distributed, shared network, many fintech start-ups are focused on developing private blockchains in 2015 that can only be accessed by pre-approved participants. GreySpark believes this trend shows a disconnect between the business imperatives of fintech start-ups to create blockchain solutions that garner widespread uptake and the desire of banks and buyside firms to support a DLT [Distributed Ledger Technology] solution designed to service every aspect of the pre- and post-trade lifecycle."12
Apparently (though I could not find what I consider to be an authoritative source on the matter), both Git and Mercuriual use specialized Merkle trees for managing versions.
 Using a hash tree like a Merkle tree:
Using a hash tree like a Merkle tree:
- significantly reduces the amount of data that a trusted authority has to maintain to proof the integrity of the data.
- significantly reduces the network I/O packet size to perform consistency and data verification as well as data synchronization.
- separates the validation of the data from the data itself -- the Merkle tree can reside locally, or on a trusted authority, or can itself reside on a distributed system (perhaps you only maintain your own tree.) Decoupling the "I can prove the data is valid" from the data itself means you can implement the appropriate and separate (including redundant) persistence for both the Merkle tree and the data store.
So the answer to the why is three-fold:
- Merkle trees provide a means of proving that integrity / validity of your data.
- Merkle trees require little memory / disk space and proofs are computationally easy and fast.
- Merkle tree proofs and management requires only a very small and terse amount of information to be transmitted across a network.
This is known as a "consistency proof" because it lets you verify that any two versions of a log are consistent:
- the later version includes everything in the earlier version
- ...in the same order
- ...and all new records come after the records in the older version7
"If you can prove that a log is consistent it means that:
- no certificates [records] have been back-dated and inserted into the log,
- no certificates have been modified in the log,
- and the log has never been branched or forked."7
A consistency proof is therefore important for verifying that your log has not been corrupted. "Monitors and auditors regularly use consistency proofs to verify that logs are behaving properly."7
This is known as an "audit proof" because it lets you verify that a specific record has been included in the log. As with the consistency verification, the server maintaining the log provides the client with a proof that the record exists in the log. "Anyone can request a Merkle audit proof from a log and verify that a certificate [record] is in the log. Auditors routinely send these types of requests to logs so they can verify certificates for TLS clients. If a Merkle audit proof fails to produce a root hash that matches the Merkle tree hash, it means the certificate is not in the log."7 (More on what a root has is and how an audit proof works later on.)

But there's another reason for sending the proof to the client: it proves that the server itself is not inventing a positive answer, but is instead proving to you, the client, that it knows what it's talking about. Faking a proof is computationally impossible.
Merkle trees are useful in synchronizing data across a distributed data store because it allows each node in the distributed system to quickly and efficiently identify records that have changed without having to send all the data to make the comparison. Instead, once a particular leaf in the tree is identified as having been changed, only the record that is associated with that specific leaf is sent over the network. Note that Merkle trees do not directly provide mechanisms for resolving collisions and synchronizing multiple writers to the same record. We'll demonstrate how this works later on.
As I mentioned above, you'll have to wait for Part II, because data synchronization is a whole article unto itself. Basic synchronization (has a leaf changed) is straight forward, but more complex synchronization in a dynamic environment where leaves can be appended or deleted (not sure an insert operation has any meaning), is a non-trivial problem. Technically, you may not want to use Merkle trees for this, particularly since it invalidates the point of an audit or consistency proof, but I think a discussion of this is still worthwhile in the context of synchronizing distributed data, when it is quite likely that a leaf, if not outright deleted, would at least be marked for deletion. So, Merkle tree garbage collection is an issue involved in data synchronization, at least in my thinking of the matter.

Critical to the concept of a consistency proof and an audit proof is that there actually is a proof that the client can verify on its own. This means that when the client queries a server (ideally a trusted authority) to validate consistency or the existence of a transaction, the server doesn't just respond with a "yes" or "no" answer, but, in the case of a "yes", sends you back a proof that the client can verify. The proof is based on the server's knowledge of the Merkle tree, which cannot be duplicated by someone trying to get the client to believe that their data is valid.
In a distributed system, each node maintains the Merkle tree for its data, and during the synchronization process, any node indicating that a record has changed ends up implicitly proving itself to the other nodes that it is a valid node. In other words, a node cannot jump onto the network and say "I have a new record" or "I have a record to replace this other record" because it is lacking the information necessary to prove itself to the other nodes.
A Merkle tree is typically a binary tree in which each leaf represents the hashed value of the record associated with that leaf. The branches are the hash of the concatenated hashes of the two children. This process of re-hashing the concatenation of the child nodes to create the parent node is performed until the top of the tree is reached, called the "root hash."

 The above diagram simulates the concatenation of the child hashes. We'll use this simulation throughout the article.
The above diagram simulates the concatenation of the child hashes. We'll use this simulation throughout the article.
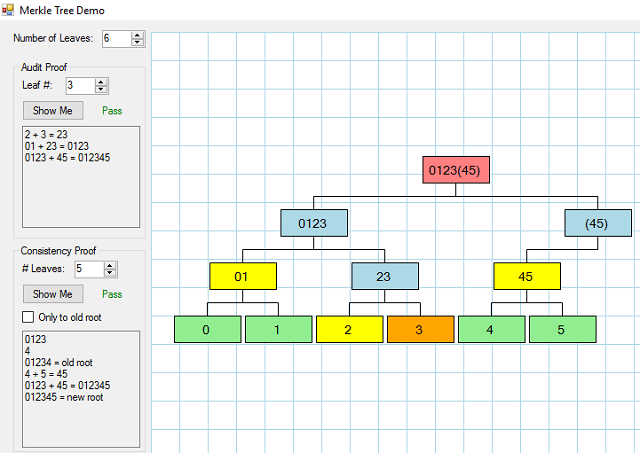
Let's say you are the owner of the record "2" in the above diagram. You also have, from a trusted authority, the root hash, which in our simulation is "01234567". You ask the server to prove to you that your record "2" is in the tree. What the server returns to you are the hashes "3", "01", "4567" as illustrated here:

Using this information (including the right-left flags that are sent back along with the hashes), the proof is that:
- 2 + 3 from which you compute 23
- 01 + 23 from which you compute 0123
- 0123 + 4567 from which you compute 01234567
Since you know the root hash from your trusted authority, the proof validates that "2" exists in the tree. Furthermore, the system from which you have obtained the proof is proving to you that it is an "authority" because it is able to provide valid hashes so that you can get from "2" to your known root hash "01234567." Any system pretending to validate your request would not be able to provide you with the intermediate hashes since you're not giving the system the root hash, you're just telling it to give you the proof - it can't invent the proof because it doesn't know your root hash -- only you know that.
In order to verify the proof, very little information about the tree is revealed to you. Furthermore, the data packet that is needed for this proof is very small, making it efficient to send over a network and to make the proof computation.
Consistency proofs apply to trees that are "append only", like a log. They are typically not used in systems where leaves are being updated because this would require synchronizing old root hash values. It's doable, it's just not something I would expect to see. Section 2.1.3 of RFC 69629 provides some useful diagrams on how a consistency proof works, but I found it confusing to figure out, so I'll try and explain it a bit better here. Using their example (but my simulated hash numbering), we'll start with 3 records:
First three records "012" are created:

A fourth record "3" is added at some point, resulting in this tree:

Two more records "45" are added:

And finally, one more record "6" is added:

For each of the sub-trees (record sets), we appended:
012
3
45
6
We have:
- The new root hash for the tree after all the sub-trees were appended and...
- The original hash of each tree before additional records were appended.
We now want to verify the root hashes when those sub-trees were added can be reconstructed, even though the full tree's root hash has changed. This verifies the order of the records and that the data associated with the record's hash hasn't changed, either on the authority server or the client's machine.
A consistency proof recreates the hashes for each sub-tree given the new tree (last figure above):
- The first tree has a root hash of "
012". - When the second tree was added, the root hash became "
0123". - When the third tree was added, the root hash changed to "
012345". - When the last tree was added, the root hash changed to "
0123456".
Consistency Proof of the First Tree
What do we need to do to verify that the first tree, with its 3 leaves, still exists in the new tree?

As the above diagram illustrates, we need the hashes of 2 nodes "01" and "2" in order to reconstruct the first tree's old root has of "012".
Consistency Proof of the Second Tree
The root hash when we added the second tree, which appended one leaf "3" for a total of 4 leaves now in the tree, was the hash for the node "0123".

The consistency proof is simply the node that represents "0123".
Consistency Proof of the Third Tree
The third tree added two nodes "45" and the root hash at that point was "012345". The consistency proof obtains that for us:

Consistency Proof Another Scenario
Let's say we added leaves "4", "5", and "6" separately. When we added the leaf for "4", we were given the hash for the node "01234" for the 5 leaves in the tree at that point. Now that we have 7 leaves in the tree, here are the pieces needed to reconstruct the old root hash of "01234":

Consistency Proof Last Scenario
This scenario differs from all the rest because three nodes are required to construct the original root hash. Given a tree with 8 leaves, where the 7th leaf (node "6") was added, the root hash at that point was the hash for "0123456". The reconstruction of this hash requires these nodes:

The last example above illustrates how the old root hash "0123456" is reconstructed from the list of nodes in the consistency proof. Here, the nodes are given to us in the following order:
0123
45
6
To reconstruct the old hash, we have to combine hashes from right to left:
45 + 6 = 456
0123 + 456 = 0123456
This is not a trivial algorithm and uses the following rules and information:
- A consistency proof is always based on a computation verifying the first m leaves in the tree. When we add a tree to an existing tree, m is the number of leaves after the trees have been combined. This is a requirement because you want to make sure that all the hashes of the data verify order and have not mutated.
- However, by knowing the number of leaves that represented the intermediate root hash, the algorithm can quickly identify the specific node that consists of either:
- the matching hash (if the number of leaves is a power of 2).
- the child pairs needed to reconstruct the intermediate root hash.
 This implies that when a tree is added to the "log" (existing set of records), the number of leaves now present in the tree are retained along with the root hash.
This implies that when a tree is added to the "log" (existing set of records), the number of leaves now present in the tree are retained along with the root hash.- In many cases, where one particular system is solely responsible for appending trees, this is simple because the system of course knows how many leaves are in each tree it is adding.
- In a distributed system, where there can be other participants appending trees (along with the added complexity of preventing simultaneous append operations) the participant adding the tree needs to be informed as to the number of leaves in the tree so that a consistency check can be performed later.
- To avoid this extra knowledge, the maintainer of the full Merkle tree can utilize a dictionary mapping tree roots that were appended to leaf counts. This is probably a more secure way of managing the required information.
On the other hand, the algorithm is very efficient because it begins with the leftmost node at the level that is log2(m). This avoids having to compute the hashes for potentially thousands of leaves starting from the first leaf, but still guarantees that if the resulting proof matches the hash when the tree was appended, the order of the records and the records themselves are valid.
You can read through the consistency proof in section 2.1.2 of RFC 69629, or you can just go with this, as illustrated by the following DRAKON diagram:

Rule 1
Find the leftmost node of the tree from which we can start our consistency proof. Usually, this will be a node representing a piece (the left piece) of the hash needed to obtain the old root hash.
Given m, the number of leaves in the master tree after a sub-tree was added, take n=log2(m) to find the index of the node representing at most m leaves. This index is the left-branch traversal up the tree, starting from the leftmost leaf, of the tree.
For example:
3 leaves: log2(3) = 1.58 (we start at node "01")
4 leaves: log2(4) = 2 (we start at node "0123")
6 leaves: log2(6) = 2.58 (we start at node "0123")
This gives you the index (rounded down) of the node whose hash you start with. By starting at the correct level, we know that the sub-tree starts at this position or is a composite -- if there's a remainder of log2(m) -- of the current node's hash and the hash of a sibling node. This diagram should help (note that level 3 is actually not representing 8 leaves, because all 8 leaves haven't been added yet):

Also, set k, the number of leaves for this node (nodes have to compute their leaf count because the last leaf of a tree might be missing.)
Also set the initial sibling node (SN) to the sibling of the node acquired by Rule 1, if it exists.
if m-k == 0, proceed with rule 3.
Three scenarios using the above diagram:
- m of 2: index = 1 (the "01" node) and it has 2 leaves, so we move on to rule 3
- m of 4: index = 2 (the "01234" node), and it has 4 leaves, so we move on to rule 3
- m of 3: index = 1 ("the "01" node) and it has 2 leaves, but m-k = 1, so we move on to rule 2
Rule 2
- if m-k == # of SN's leaves, concatenate the hash of SN and exit Rule 2, as this represents the hash of the old root
- if m-k < # of SN's leaves, set SN to SN's left child node and repeat Rule 2
- if m-k > # of SN's leaves, concatenate the hash of SN, increment k by SN's # of leaves, and set SN to its parent's right node
In this manner, we always end of with the hashes from which we can reconstruct the old root hash.
A few scenarios:
m = 3. k=2 (the number of leaves under "01"), SN = "23"
SN's # of leaves is 2. m-k < 2, so SN = left child of SN, which is "2"
SN's # of leaves is 1(well, it is a leaf)
m-k = SN's # of leaves, so we know to use the hash for "01" plus the hash for "2" to construct the old root "012".
m = 4 is handled by rule 1
m = 5. k=4 (the number of leaves under "0123"). SN="456"
SN's # of leaves is 3.
m-k < SN's # of leaves, so SN = left child of SN, which is "45"
SN's # of leaves is now 2
m-k < SN's # of leaves, so SN = left child of SN, which is "4"
SN's # of leaves is now 1 (it's a leaf)
m-k = SN's # of leaves, so we know to use the hash for "0123" plus the hash for "4" to construct the old root "01234".
This is a good example of constructing a consistency tree for any number of leaves starting from the first leaf, whether the old root was part of a tree that was added to the master tree or not. However, this is not the typical scenario. Moving along:
m = 6. k=4 (the number of leaves under "0123"). SN="456"
SN's # of leaves is 3.
m-k < SN's # of leaves, so SN = left child of SN, which is "45"
SN's # of leaves is now 2.
m-k - SN's # of leaves, so we know to use the hash for "0123" plus the hash for "45" to construct the old root "012345".
m = 7. k=4 (the number of leaves under "0123"). SN="456"
m-k = SN's # of leaves, so we know to use the hash for "0123" plus the hash for "456" to construct the existing root "0123456"
Rule 3: Continue with the audit proof (using the appropriate left or right sibling) for the node (not necessarily a leaf) of the last node in the consistency proof.
For example, given this consistency proof to the old hash for the tree representing "01234" (this is the more interesting example):

The nodes involved in the remainder of the proof, so that we obtain the root hash, are the hashes of the nodes "5" and "67".

We need "5" to obtain "45", and we need "67" to obtain "4567". Cool stuff!

The demo lets you explore creating Merkle trees and performing audit and consistency proofs. The graphic surface is implemented as an embedded FlowSharp service.
 The demo communicates with the FlowSharp service using a websocket on port 1100 for the purpose of creating shapes and connectors on the canvas. You will probably see the Windows Firewall alert when you first run the demo.
The demo communicates with the FlowSharp service using a websocket on port 1100 for the purpose of creating shapes and connectors on the canvas. You will probably see the Windows Firewall alert when you first run the demo.

Please click on "Allow access."

You can select up to 16 leaves. The leaf simulated hashes are represented as 0-F for rendering convenience.

You can test an audit proof by selecting the leaf you wish to audit (the leaf number selection is 0-15, where 10-15 are represented as A-F on the graph.) When you click on Show Me, the proof is displayed and the verification routine is run. The graph also shows you the nodes involved in performing the audit proof (see the numerous screenshots above.)

You can test a consistency proof by selecting the number of leaves for which you wish to test the consistency. The nodes involved in computing the old root are indicated in yellow, the nodes for finishing the proof using the audit proof are shown in purple:

The checkbox "only to root node" is basically just for making it easy to create the screenshots where I discuss the first have of the consistency proof -- you don't get the purple nodes involved in the second step, the audit proof.
What follows is the implementation of the Merkle tree. There are three classes:
MerkleHashMerkleNodeMerkleTree
Let's look at each.
This class provides a few static create operators, equality tests, and of course computes the hash from a byte array, string, or two other MerkleHash instances.
namespace Clifton.Blockchain
{
public class MerkleHash
{
public byte[] Value { get; protected set; }
protected MerkleHash()
{
}
public static MerkleHash Create(byte[] buffer)
{
MerkleHash hash = new MerkleHash();
hash.ComputeHash(buffer);
return hash;
}
public static MerkleHash Create(string buffer)
{
return Create(Encoding.UTF8.GetBytes(buffer));
}
public static MerkleHash Create(MerkleHash left, MerkleHash right)
{
return Create(left.Value.Concat(right.Value).ToArray());
}
public static bool operator ==(MerkleHash h1, MerkleHash h2)
{
return h1.Equals(h2);
}
public static bool operator !=(MerkleHash h1, MerkleHash h2)
{
return !h1.Equals(h2);
}
public override int GetHashCode()
{
return base.GetHashCode();
}
public override bool Equals(object obj)
{
MerkleTree.Contract(() => obj is MerkleHash, "rvalue is not a MerkleHash");
return Equals((MerkleHash)obj);
}
public override string ToString()
{
return BitConverter.ToString(Value).Replace("-", "");
}
public void ComputeHash(byte[] buffer)
{
SHA256 sha256 = SHA256.Create();
SetHash(sha256.ComputeHash(buffer));
}
public void SetHash(byte[] hash)
{
MerkleTree.Contract(() => hash.Length == Constants.HASH_LENGTH,
"Unexpected hash length.");
Value = hash;
}
public bool Equals(byte[] hash)
{
return Value.SequenceEqual(hash);
}
public bool Equals(MerkleHash hash)
{
bool ret = false;
if (((object)hash) != null)
{
ret = Value.SequenceEqual(hash.Value);
}
return ret;
}
}
}
This class manages everything about a node -- it's parent, children, and of course it's hash. The only really interesting feature of the MerkleNode class is that it implements a bottom-up/left-right iterator.
namespace Clifton.Blockchain
{
public class MerkleHash
{
public byte[] Value { get; protected set; }
protected MerkleHash()
{
}
public static MerkleHash Create(byte[] buffer)
{
MerkleHash hash = new MerkleHash();
hash.ComputeHash(buffer);
return hash;
}
public static MerkleHash Create(string buffer)
{
return Create(Encoding.UTF8.GetBytes(buffer));
}
public static MerkleHash Create(MerkleHash left, MerkleHash right)
{
return Create(left.Value.Concat(right.Value).ToArray());
}
public static bool operator ==(MerkleHash h1, MerkleHash h2)
{
return h1.Equals(h2);
}
public static bool operator !=(MerkleHash h1, MerkleHash h2)
{
return !h1.Equals(h2);
}
public override int GetHashCode()
{
return base.GetHashCode();
}
public override bool Equals(object obj)
{
MerkleTree.Contract(() => obj is MerkleHash, "rvalue is not a MerkleHash");
return Equals((MerkleHash)obj);
}
public override string ToString()
{
return BitConverter.ToString(Value).Replace("-", "");
}
public void ComputeHash(byte[] buffer)
{
SHA256 sha256 = SHA256.Create();
SetHash(sha256.ComputeHash(buffer));
}
public void SetHash(byte[] hash)
{
MerkleTree.Contract(() =>
hash.Length == Constants.HASH_LENGTH, "Unexpected hash length.");
Value = hash;
}
public bool Equals(byte[] hash)
{
return Value.SequenceEqual(hash);
}
public bool Equals(MerkleHash hash)
{
bool ret = false;
if (((object)hash) != null)
{
ret = Value.SequenceEqual(hash.Value);
}
return ret;
}
}
}
This class is responsible for building the tree and performing the audit and consistency proofs. A couple static methods are used for verifying an audit and consistency proof, so you don't have to write the verification algorithms yourself. I've broken down the class into its constituent components.
namespace Clifton.Blockchain
{
public class MerkleTree
{
public MerkleNode RootNode { get; protected set; }
protected List<MerkleNode> nodes;
protected List<MerkleNode> leaves;
That's it - very simple.
public static void Contract(Func<bool> action, string msg)
{
if (!action())
{
throw new MerkleException(msg);
}
}
I use this method for parameter and state verification.
public MerkleTree()
{
nodes = new List<MerkleNode>();
leaves = new List<MerkleNode>();
}
public MerkleNode AppendLeaf(MerkleNode node)
{
nodes.Add(node);
leaves.Add(node);
return node;
}
public void AppendLeaves(MerkleNode[] nodes)
{
nodes.ForEach(n => AppendLeaf(n));
}
public MerkleNode AppendLeaf(MerkleHash hash)
{
var node = CreateNode(hash);
nodes.Add(node);
leaves.Add(node);
return node;
}
public List<MerkleNode> AppendLeaves(MerkleHash[] hashes)
{
List<MerkleNode> nodes = new List<MerkleNode>();
hashes.ForEach(h => nodes.Add(AppendLeaf(h)));
return nodes;
}
public MerkleHash AddTree(MerkleTree tree)
{
Contract(() => leaves.Count > 0, "Cannot add to a tree with no leaves.");
tree.leaves.ForEach(l => AppendLeaf(l));
return BuildTree();
}
public MerkleHash BuildTree()
{
Contract(() => leaves.Count > 0, "Cannot build a tree with no leaves.");
BuildTree(leaves);
return RootNode.Hash;
}
protected void BuildTree(List<MerkleNode> nodes)
{
Contract(() => nodes.Count > 0, "node list not expected to be empty.");
if (nodes.Count == 1)
{
RootNode = nodes[0];
}
else
{
List<MerkleNode> parents = new List<MerkleNode>();
for (int i = 0; i < nodes.Count; i += 2)
{
MerkleNode right = (i + 1 < nodes.Count) ? nodes[i + 1] : null;
MerkleNode parent = CreateNode(nodes[i], right);
parents.Add(parent);
}
BuildTree(parents);
}
}
public List<MerkleProofHash> AuditProof(MerkleHash leafHash)
{
List<MerkleProofHash> auditTrail = new List<MerkleProofHash>();
var leafNode = FindLeaf(leafHash);
if (leafNode != null)
{
Contract(() => leafNode.Parent != null, "Expected leaf to have a parent.");
var parent = leafNode.Parent;
BuildAuditTrail(auditTrail, parent, leafNode);
}
return auditTrail;
}
protected void BuildAuditTrail(List<MerkleProofHash> auditTrail,
MerkleNode parent, MerkleNode child)
{
if (parent != null)
{
Contract(() => child.Parent == parent, "Parent of child is not expected parent.");
var nextChild = parent.LeftNode == child ? parent.RightNode : parent.LeftNode;
var direction = parent.LeftNode == child ? MerkleProofHash.Branch.Left :
MerkleProofHash.Branch.Right;
if (nextChild != null)
{
auditTrail.Add(new MerkleProofHash(nextChild.Hash, direction));
}
BuildAuditTrail(auditTrail, child.Parent.Parent, child.Parent);
}
}
Consistency Proof
public List<MerkleProofHash> ConsistencyProof(int m)
{
List<MerkleProofHash> hashNodes = new List<MerkleProofHash>();
int idx = (int)Math.Log(m, 2);
MerkleNode node = leaves[0];
while (idx > 0)
{
node = node.Parent;
--idx;
}
int k = node.Leaves().Count();
hashNodes.Add(new MerkleProofHash(node.Hash, MerkleProofHash.Branch.OldRoot));
if (m == k)
{
}
else
{
MerkleNode sn = node.Parent.RightNode;
bool traverseTree = true;
while (traverseTree)
{
Contract(() => sn != null, "Sibling node must exist because m != k");
int sncount = sn.Leaves().Count();
if (m - k == sncount)
{
hashNodes.Add(new MerkleProofHash(sn.Hash, MerkleProofHash.Branch.OldRoot));
break;
}
if (m - k > sncount)
{
hashNodes.Add(new MerkleProofHash(sn.Hash, MerkleProofHash.Branch.OldRoot));
sn = sn.Parent.RightNode;
k += sncount;
}
else
{
sn = sn.LeftNode;
}
}
}
return hashNodes;
}
public List<MerkleProofHash> ConsistencyAuditProof(MerkleHash nodeHash)
{
List<MerkleProofHash> auditTrail = new List<MerkleProofHash>();
var node = RootNode.Single(n => n.Hash == nodeHash);
var parent = node.Parent;
BuildAuditTrail(auditTrail, parent, node);
return auditTrail;
}
Verify Audit Proof
public static bool VerifyAudit(MerkleHash rootHash, MerkleHash leafHash,
List<MerkleProofHash> auditTrail)
{
Contract(() => auditTrail.Count > 0, "Audit trail cannot be empty.");
MerkleHash testHash = leafHash;
foreach (MerkleProofHash auditHash in auditTrail)
{
testHash = auditHash.Direction == MerkleProofHash.Branch.Left ?
MerkleHash.Create(testHash.Value.Concat(auditHash.Hash.Value).ToArray()) :
MerkleHash.Create(auditHash.Hash.Value.Concat(testHash.Value).ToArray());
}
return rootHash == testHash;
}
public static List<Tuple<MerkleHash, MerkleHash>> AuditHashPairs
(MerkleHash leafHash, List<MerkleProofHash> auditTrail)
{
Contract(() => auditTrail.Count > 0, "Audit trail cannot be empty.");
var auditPairs = new List<Tuple<MerkleHash, MerkleHash>>();
MerkleHash testHash = leafHash;
foreach (MerkleProofHash auditHash in auditTrail)
{
switch (auditHash.Direction)
{
case MerkleProofHash.Branch.Left:
auditPairs.Add(new Tuple<MerkleHash, MerkleHash>(testHash, auditHash.Hash));
testHash = MerkleHash.Create
(testHash.Value.Concat(auditHash.Hash.Value).ToArray());
break;
case MerkleProofHash.Branch.Right:
auditPairs.Add(new Tuple<MerkleHash, MerkleHash>(auditHash.Hash, testHash));
testHash = MerkleHash.Create
(auditHash.Hash.Value.Concat(testHash.Value).ToArray());
break;
}
}
return auditPairs;
}
public static bool VerifyConsistency(MerkleHash oldRootHash, List<MerkleProofHash> proof)
{
MerkleHash hash, lhash, rhash;
if (proof.Count > 1)
{
lhash = proof[proof.Count - 2].Hash;
int hidx = proof.Count - 1;
hash = rhash = MerkleTree.ComputeHash(lhash, proof[hidx].Hash);
hidx -= 2;
while (hidx >= 0)
{
lhash = proof[hidx].Hash;
hash = rhash = MerkleTree.ComputeHash(lhash, rhash);
--hidx;
}
}
else
{
hash = proof[0].Hash;
}
return hash == oldRootHash;
}
protected MerkleNode FindLeaf(MerkleHash leafHash)
{
return leaves.FirstOrDefault(l => l.Hash == leafHash);
}
protected virtual MerkleNode CreateNode(MerkleHash hash)
{
return new MerkleNode(hash);
}
protected virtual MerkleNode CreateNode(MerkleNode left, MerkleNode right)
{
return new MerkleNode(left, right);
}
In bitcoin, a tree always has an even number of leaves. If the last leaf in the tree is the left branch, then that last leaf is duplicated into the right leaf position, and the parent's hash is therefore computed from the concatenation of same the (left branch) hash. You can use FixOddNumberLeaves to create this behavior.
public void FixOddNumberLeaves()
{
if ((leaves.Count & 1) == 1)
{
var lastLeaf = leaves.Last();
var l = AppendLeaf(lastLeaf.Hash);
}
}
Other Stuff - Compute Hash Given Two Hashes
public static MerkleHash ComputeHash(MerkleHash left, MerkleHash right)
{
return MerkleHash.Create(left.Value.Concat(right.Value).ToArray());
}
This class is used by the audit proof, associating the left/right branch with the proof hash, which is necessary to concatenate the two child hashes in the correct order to obtain the parent hash.
namespace Clifton.Blockchain
{
public class MerkleProofHash
{
public enum Branch
{
Left,
Right,
OldRoot,
}
public MerkleHash Hash { get; protected set; }
public Branch Direction { get; protected set; }
public MerkleProofHash(MerkleHash hash, Branch direction)
{
Hash = hash;
Direction = direction;
}
public override string ToString()
{
return Hash.ToString();
}
}
}

There are 14 unit tests, some of which are silly and most of which are trivial. The most interesting unit test is the one for the consistency proof, so that's the only one I'm going to describe here.
 This unit test creates trees with 3 to 100 leaves and for each tree, tests that the old root can be obtained for leaves [1, n-1] where n is the number of leaves in the test tree.
This unit test creates trees with 3 to 100 leaves and for each tree, tests that the old root can be obtained for leaves [1, n-1] where n is the number of leaves in the test tree.
[TestMethod]
public void ConsistencyTest()
{
MerkleTree tree = new MerkleTree();
var startingNodes = tree.AppendLeaves(new MerkleHash[]
{
MerkleHash.Create("1"),
MerkleHash.Create("2"),
});
MerkleHash firstRoot = tree.BuildTree();
List<MerkleHash> oldRoots = new List<MerkleHash>() { firstRoot };
for (int i = 2; i < 100; i++)
{
tree.AppendLeaf(MerkleHash.Create(i.ToString()));
tree.BuildTree();
oldRoots.ForEachWithIndex((oldRootHash, n) =>
{
List<MerkleProofHash> proof = tree.ConsistencyProof(n+2);
MerkleHash hash, lhash, rhash;
if (proof.Count > 1)
{
lhash = proof[proof.Count - 2].Hash;
int hidx = proof.Count - 1;
hash = rhash = MerkleTree.ComputeHash(lhash, proof[hidx].Hash);
hidx -= 2;
while (hidx >= 0)
{
lhash = proof[hidx].Hash;
hash = rhash = MerkleTree.ComputeHash(lhash, rhash);
--hidx;
}
}
else
{
hash = proof[0].Hash;
}
Assert.IsTrue(hash == oldRootHash, "Old root hash not found for index "
+ i + " m = " + (n+2).ToString());
});
oldRoots.Add(tree.RootNode.Hash);
}
}
Hash trees are one way of creating efficient proofs of data integrity. Monotonic (sequentially ordered) can be an appropriate way of working with hash chains as well. One such example is Holochain "...a validating monotonic DHT 'backed' by authoritative hashchains.."14 Holochain is "...a shared DHT in which each piece of data is rooted in the signed hash chain of one or more parties. It is a validating DHT so data cannot propagate without first being validated by shared validation rules held by every node"13 As such, it is possible to combine the two techniques (monotonic hash chains and hash trees) together. As Arthur wrote to me over Slack:
Merkle trees can be used inside a holochain entry to have truly PRIVATE data (not just encrypted), in a shared chain space. What I mean by this is... Suppose you have a data structure with these 6 fields:
- Sender_ID
- Sender_Previous_Hash
- Receiver_ID
- Receiver_Previous_Hash
- Number_Credits_Sent
- Transaction_Payload
If you structured these in a Merkle tree with these 6 leaves, you could have both parties to the transaction commit the full transaction to their private chains, and then both people put and sign a partial Merkle tree to the shared DHT which does NOT contain the leaf node for field #6. This would be adequate for doing a Merkle proof on the first 5 fields which need to be published for managing the currency, allowing them to have digital assets, or any other type of data in the hidden field which can ALWAYS stay hidden on your local chain, visible only to you, without compromising the integrity of the data needed to manage the mutual credit cryptocurrency.
On blockchains, all the data in the transaction goes onto the chain and you have to encrypt the parts you want to keep private, and hope that neither your keys nor the encryption scheme you've used are ever compromised on this permanent, public record. On a holochain, because of the mechanism of the shared DHT being 'backed" by data validation from local chains, you have the possibility of using Merkle proofs to blend public/private data in ways which let you actually keep the private data private.
Bitcoin, Ethereum, and other blockchains are also examples of a monotonic hash chain (the chain of blocks) that contain within them a Merkle tree of transactions.
Writing this article was definitely the embodiment of the experience "you only understand it if you can teach it." It took a lot of research and digging to understand not just the algorithms, specifically for the consistency proof. More importantly, understanding the "why" was not intuitively obvious. I ended up doing a mental Q&A session with myself, which I decided to add here just so you can see what my basic questions were and how I decided to answer them, at least for myself. Some of these answer may not be very good, some may go down unnecessary rabbit holes, etc., so keep in mind that this represents a snapshot of my own investigation before even starting this article.
Before you read my probably bizarre though process below, one more concluding thought -- blockchains and their variants are, in my opinion, destined to become a core component in distributed data management. Merkle trees and similar hash tree implementations are a cornerstone to how this technology works.
Data Synchronization Q&A
- As the "client", you're downloading a large file, say 10GB, spread across peers in chunks of 4096 bytes.
- You need a trusted authority server to tell you whether each block is valid.
- From the server, you can be given the root hash and, as each block comes in, you start filling in the Merkle tree yourself.
- However, you'll need all the data downloaded before you can complete the tree to verify the root.
- Instead, you can ask the server to send you the path of a hashed chunk (the leaf) to the root hash and verify it yourself. This enables you to verify each chunk and if it is faulty, request it from somewhere else, simultaneously while you are downloading other chunks. Furthermore, you're not maintaining all the hashes of the chunks and building the entire Merkle tree yourself. So it's faster for verifying a chunk, and it's less memory on your part to hold the entire Merkle tree.
- The server (as trusted authority) doesn't hold the data, but it has to have the Merkle tree, including leaf hashes.
With regards to data synchronization, you basically have three options:
- Download all the data so you can verify the Merkle root hash
- Download from a trusted authority the Merkle tree so you can test with an incomplete recordset.
- Ask the server to perform an audit proof on a particular leaf.
Validation Q&A
Q1: Why not just ask the server if the leaf exists in tree with the specific root?
Q2: Why should the server even bother with storing a Merkle tree of the leaf hashes? (see answer to Q4 as well)
A1: You could do that, but the SHA256 hash is only 32 bytes, and while this represents a huge number of unique hashes (2^256), 1.15*10^77, hashing node pair hashes as we walk up the tree strongly validates that the hash under question belongs to the correct tree. Furthermore, the audit proof verifies the particular order of the record in relationship to the other leaves. We don't just want to know that a leaf exists, we want to verify that it exists in a particular location in the tree.
A2: Let's say you have a large dataset divided into small chunks. First, you may not be maintaining the entire dataset but only the portion you are responsible for. If a change occurs in that chunk, you can recalculate the root hash knowing only the left-right branches to the root.
The side-effect to this is that you also only need to maintain the left-right branches for your chunks, rather than the entire Merkle tree (including all the leaf hashes of chunks that you don't know or care about.)
To synchronize, another user asks you to verify your root hash against their root hash. If different, the left/right child hashes are requested, and the process iterates the mismatches until the chunks on your end that have changed are identified. Now you only send your changed chunk to the other user, and you are both synchronized again.
Detect Collisions Q&A
Q3: What happens if more than one user modifies the same chunk (based on the idea that in a distributed system, you want to replicate the data across many peers for resiliency.)
A1: Only one peer may have the authority to change the data.
A2: Hashes can be time stamped, and you accept only the most recent change, discarding anything else.
A3: Differences are merged (either automatically or requiring manual intervention.)
A4: You accept only the oldest change, and discard anything more recent.
A5: Technically, a chunk should never be changed. If a change is required, this should be logged as a new transaction so that there is an auditable trail of changes (not the same think as a Merkle audit). Given that, only specified authorities should be allowed to modify a transaction.
A6: Some sort of blocking mechanism might be used to prevent data from being modified simultaneously. For example, you could be given a "change key" and when you submit the change, if your change key doesn't match the current change key, your change is rejected, requiring you to syncrhonize your data, acquire a new change key, and submit your changes again.
A7: The salient point to this is that, if the chunk sizes are small, the likelihood that your change will collide with someone else's is small.
Why Proofs Q&A
Q4: Why should the server send you the hash audit trail of to verify a chunk, rather than just sending you a "yes/no" response?
A: This is your way of verifying that the server hasn't been compromised -- if it simply said "yes", how would you know you can trust it? By sending you the left-right hashes, the server is telling you "here is how I verified your request." A server that is trying to get you to believe your chunk has is valid cannot send you "any" audit trail hash because that would give a different root hash.
- 13th March, 2017: Initial version
