The code presented in this article is ASM (assembly language) and can easily adaptable to any language that supports SSE, in particular AVX. If basic matrix multiplication is any indicator, huge performance gains result. I created my own version of the XMMatrixMultiply function and saw a 657% speed improvement. In a 3D scene, XMMatrixMultiply is called a lot. Through this article I use matrix multiplication to demonstrate the difference in speed.
Sloppy Shortcuts or Shining Quality?
The software development establishment (particularly academia) has always worshipped at the altar of laziness and avoiding work. Use somebody else’s library! Don’t reinvent the wheel! Let the compiler do it! Dogma has a nasty habit of perpetuating itself, steadily degrading output quality further and further until the end product becomes so diminished as to be effectively unusable.
There was a time when skill, knowledge, and craftsmanship were honored traditions. Pride in workmanship was the quintessential opposite of laziness and shoddy shortcuts. What happens if these concepts are applied to the 3D math of today?
If basic matrix multiplication is any indicator, huge performance gains result. I created my own version of the XMMatrixMultiply function and saw a 657% speed improvement. In a 3D scene, XMMatrixMultiply is called a lot. Speeding it up 6.57 times (as it measured on my test machine) is going to be noticed. And that’s just one function in a math library that has 42 additional functions devoted to matrix handling alone.
Pseudo-Code Inside
The code presented in this article is ASM (assembly language), for the primary reason that it's much easier to read and follow than overly-adorned and complicated intrinsics. For the purposes of relating a concept, using ASM is much cleaner than trying to muddle through long lists of intrinsics. The code herein is easily adaptable to any language that supports SSE, in particular AVX.
A complete .DLL, .LIB, C++ header file, and instructions accompany this article and are available for download. The PCC_XMMatrixMultiply function presented in this article is included in that download. It takes the same input and provides the same output as the DirectXMath function XMMatrixMultiply.
Thinking Outside the Matrix
SSE (Streaming SIMD [Single Instruction Multiple Data] Extensions) is a mixed blessing. It does a lot of work with a lot of data in a very short time. Working with SSE is simple enough in theory, but the real challenge lies in keeping track of exactly what’s going on with all that data during extensive operations.
As SSE has evolved into AVX (Advanced Vector Extensions), AVX2, and AVX-512 beyond that, more and more functionality has been added that’s highly conducive to vector math. However, support for these processes depends on the CPU version. This article assumes AVX support with 256-bit YMM registers, holding four “slots” of double-precision float values.
Less is Not More
A common misconception, especially when using high level languages, is that reducing the instruction count inherently equates to better, faster code. This is far from being the case. Ten logical bitwise instructions will execute in a fraction of the time it takes a single memory access to complete. The number of instructions is irrelevant; a low instruction count can be slow or it can be fast, all depending on the instructions being coded. In the end, all that matters is how fast a function runs on the whole. This is the basis for the function outlined here – the instruction count may look intimidating, but when each one executes in five or six CPU cycles, the function as a whole screams through to completion in a fraction of the time it takes the DirectXMath equivalent to execute.
Stay Out of Memory
The real key to maximizing performance is to avoid memory hits. Moving data around the CPU’s registers is mega-fast, but using memory to assist the process will seriously drag down the task of multiplying two matrices (or any other operation using SSE).
In a perfect world, matrix multiplication would involve only twelve memory access operations, assuming double precision float values working with YMM registers (single precision floats using XMM would yield the same result with lower precision). There would be 8 reads, to move the four rows of the multiplier matrix M1 and the four rows of the multiplicand matrix M2 into their target registers. The final four accesses to memory would be writes, to output the final result matrix. Everything else would occur within the SSE registers.
Can this be done?
Flipping M2
The nature of matrix multiplication, on its face, precludes the efficient use of SSE instructions because of the need to work with columns, not rows, in the second matrix (M2, the multiplicand). However, if M2 can be flipped 180 degrees on an imaginary diagonal axis running from the upper left to lower right corners, then the four columns of that matrix become rows and are then fully accessible to the SSE registers.
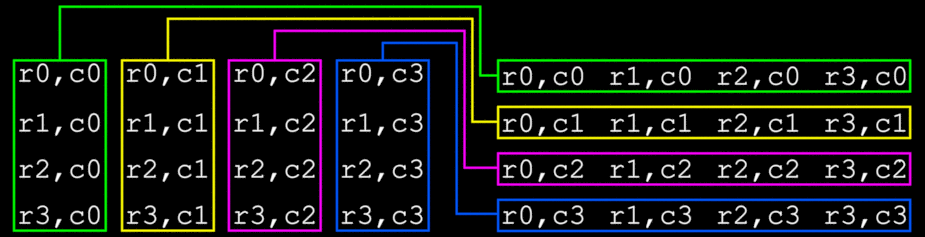
During the flip process, M2[r0,c0], M2[r1,c1], M2[r2,c2], and M2[r3,c3] don’t move. For the remainder of the values, register contents can be exchanged directly to complete the flip.
SSE works with two basic data types: packed, where distinct values are placed into each of the 64-bit slots of a YMM register, or scalar, where only the low 64 bits are used. The process of flipping M2 uses both types of instructions.
The vpermq instruction is used to rotate the content of YMM registers so that each successive value being worked with is moved to the low 64 bits of its register. Once there, scalar instructions can be used to exchange register contents. By using this approach, no data is lost or overwritten, there is no memory access, and the task of flipping M2 can be completed very quickly. The instruction count may seem high, but the total execution time is extremely low.
First, this example loads M1 rows 0-3 into YMM0, YMM1, YMM2, and YMM3. The rows of M2 are loaded into YMM4, YMM5, YMM6 and YMM7.

(This code assumes that on entry to the function, RCX points to M1 and RDX points to M2. This is standard calling convention when M1 and M2 are passed as parameters.)
vmovapd ymm4, ymmword ptr [ rdx ] ; Load M2 [ r0 ] into ymm4
vmovapd ymm5, ymmword ptr [ rdx + 32 ] ; Load M2 [ r1 ] into ymm5
vmovapd ymm6, ymmword ptr [ rdx + 64 ] ; Load M2 [ r2 ] into ymm6
vmovapd ymm7, ymmword ptr [ rdx + 96 ] ; Load M2 [ r3 ] into ymm7
With M2 loaded into memory, the flipping process can begin. The following exchanges have to be made:
r1, c0 : r0, c1
r2, c0 : r0, c2
r3, c0 : r0, c3
r2, c1 : r1, c2
r3, c1 : r1, c3
r3, c2 : r2, c3
A total of six exchanges need to be made.
An important item to remember is the little-endian operation of the CPU. Column 3 values will occupy the high 64 bits of their respective YMM registers; column 0 values will occupy the low 64 bits. This is reversed from how the matrix is viewed in diagrams and figures. Actual YMM contents are as follows:

Each value to be swapped must be rotated into the low end position of its YMM register – bits 63-0. For the first exchange, (r1,c0 with r0,c1), the value for r1,c0 is already in the low 64 bits of YMM5. YMM4 needs a 64 bit rotation right, to move the value for r0,c1 into its low 64 bits.
vpermq ymm4, ymm4, 39h ; Rotate ymm4 right 64 bits
movsd xmm8, xmm5 ; Move r1c0 to hold
movsd xmm5, xmm4 ; Move r0c1 to r1c0 in xmm5
movsd xmm4, xmm8 ; Move r1c0 to r0c1
SSE instructions use only the low 128 bits, or the XMM register portion, for scalar moves since only bits 63-0 are worked with. With YMM registers being a superset of XMM, the desired effect is achieved: values are moved between the low 64 bits of YMM registers, even though XMM registers are referenced.
After the rotation, r0c1 (in ymm8) has been rotated right so that c1 is now in bits 63-0. The next rotation to the right 64 bits places r0c2 into bits 63-0 and the process can repeat to exchange r0,c2 with r2,c0:
vpermq ymm4, ymm4, 39h ; Rotate ymm4 right 64 bits
movsd xmm8, xmm6 ; Move r2c0 to hold
movsd xmm6, xmm4 ; Move r0c2 to r2c0
movsd xmm4, xmm8 ; Move hold to r0c2
This process repeats, using YMM7 to exchange r3,c0 with r0,c3. The remainder of the M2 value exchanges proceed the same way. The final code at the end of the article contains the entire process.
Executing the Multiplication
Once M2 has been flipped, the actual multiplication can be performed. This is where the real time savings occur, because only four multiplication operations need to be performed. Since each column of M2 is now contiguous in a YMM register, direct multiplication can be applied.
First, M1 is loaded into YMM0 through YMM3:
vmovapd ymm0, ymmword ptr [ rcx ] ; Load row 0 into ymm0
vmovapd ymm1, ymmword ptr [ rcx + 32 ] ; Load row 1 into ymm1
vmovapd ymm2, ymmword ptr [ rcx + 64 ] ; Load row 2 into ymm2
vmovapd ymm3, ymmword ptr [ rcx + 96 ] ; Load row 3 into ymm3
First, multiply M1[r0], loaded into YMM0, by M2[c0], loaded into YMM4:
vmulpd ymm8, ymm0, ymm4 ; Set M1r0 * M2c0 in ymm8
With the result of M1[r1] * M2[c0] now present in YMM8, the next challenge is to accumulate the values in YMM8, which holds the result of the multiplication.
I’ve seen a lot of messy approaches to doing this; I personally found none of them suitable. For this function, I once again turn to systematically rotating the result register, YMM8, three times, by 64 bits each time, using the addsd instruction to accumulate each value that shifts into bits 63-0. Since the original M1 rows are in YMM0 – YMM3, and the post-flip M2 columns are in YMM4 – YMM7, YMM8 is discarded after the accumulation completes; it can be left in its final state, right-shifted by 192 bits.
Once again, keep in mind that no memory hits are taking place. Everything done is register-to-register and that’s where the speed-up comes from.
movsd xmm9, xmm8 ; Get the full result (only care about 63 - 0)
vpermq ymm8, ymm8, 39h ; Rotate ymm8 right 64 bits
addsd xmm9, xmm8 ; Add 127 – 64
vpermq ymm8, ymm8, 39h ; Rotate ymm8 right 64 bits
addsd xmm9, xmm8 ; Add 191 – 128
vpermq ymm8, ymm8, 39h ; Rotate ymm8 right 64 bits
addsd xmm9, xmm8 ; Add 255 - 192
The same process is repeated: multiply M1[r0] * M2[c1]. At the beginning of the process, the accumulator YMM9 is shifted left 64 bits so that the result of M1[r0] * M2[c1] can be placed into bits 63-0:
vmulpd ymm8, ymm0, ymm5 ; Set M1r0 * M2c1
vpermq ymm9, ymm9, 39h ; Rotate accumulator left 64 bits
movsd xmm9, xmm8 ; Get the full result
vpermq ymm8, ymm8, 39h ; Rotate ymm0 right 32 bits
addsd xmm9, xmm8 ; Add 63 – 32
vpermq ymm8, ymm8, 39h ; Rotate ymm0 right 32 bits
addsd xmm9, xmm8 ; Add 95 – 64
vpermq ymm8, ymm8, 39h ; Rotate ymm0 right 32 bits
addsd xmm9, xmm8 ; Add 127 – 96
This process systematically repeats two more times, using M2[c2] (YMM6) and M2[c3] (YMM7) as the multiplicands. When the process has repeated four times, each time using YMM0 as the multiplier, the accumulator YMM9 has rotated right three times. One final rotation leaves it in final form, ready to store in the final output:
vpermq ymm9, ymm9, 39h ; Rotate accumulator left 32 bits
vmovapd ymmword ptr M, ymm9 ; Store output row 0
The process repeats for output rows one, two, and three, with the multiplier moving from YMM0 to YMM1, then YMM2, then YMM3 for each row.
The end result is the output matrix M is properly computed in a fraction of the time that would be required for XMMatrixMultiply to execute.
Note: For those wishing to make their own speed comparisons, 64-bit assembly is not permitted in 64 bit Visual Studio apps, and intrinsics may or may not skew the timing results (they will probably execute slower). Further, while I cannot prove this absolutely, my experience has always been that apps written inside Visual Studio have a special relationship with Windows, where they run considerably faster than apps written with anything else. That’s been my experience; I could not stand up in a court of law and prove it so I cannot claim with authority that it’s true. It’s a firm belief that I personally hold.
The complete code listings for the PCC_XMMatrixMultiply function is shown below. Initial appearances make it look like this function has so many instructions, it couldn't possibly run in any kind of appreciable time frame. But it's not the case. These are extremely high-speed, low-latency instructions and they are cut through like greased lightning. As stated earlier, the only thing to judge by is the final performance of the function as a whole.
align qword
PCC_XMMatrixMultiply proc
; 64-bit calling conventions have RCX > M1 and RDX > M2 on entry to this function.
;*****[Load M2 into ymm4 / ymm5 / ymm6 / ymm7]*****
vmovapd ymm4, ymmword ptr [ rdx ]
vmovapd ymm5, ymmword ptr [ rdx + 32 ]
vmovapd ymm6, ymmword ptr [ rdx + 64 ]
vmovapd ymm7, ymmword ptr [ rdx + 96 ]
;*****[Swap r0,c1 and r1,c0]*************************
vpermq ymm4, ymm4, 39h
movsd xmm9, xmm5
movsd xmm5, xmm4
movsd xmm4, xmm9
;*****[Swap r0,c2 and r2,c0]*************************
vpermq ymm4, ymm4, 39h
movsd xmm9, xmm6
movsd xmm6, xmm4
movsd xmm4, xmm9
;*****[Swap r3,c0 and r0,c3]*************************
vpermq ymm4, ymm4, 39h
movsd xmm9, xmm7
movsd xmm7, xmm4
movsd xmm4, xmm9
vpermq ymm4, ymm4, 39h
;*****[Swap r2,c1 and r1,c2]*************************
vpermq ymm5, ymm5, 04Eh
vpermq ymm6, ymm6, 039h
movsd xmm9, xmm6
movsd xmm6, xmm5
movsd xmm5, xmm9
;*****[Swap r3,c1 and r1,c3]*************************
vpermq ymm5, ymm5, 039h
vpermq ymm7, ymm7, 039h
movsd xmm9, xmm7
movsd xmm7, xmm5
movsd xmm5, xmm9
vpermq ymm5, ymm5, 039h
;*****[Swap r3,c2 and r2,c3]*************************
vpermq ymm6, ymm6, 04Eh
vpermq ymm7, ymm7, 039h
movsd xmm9, xmm7
movsd xmm7, xmm6
movsd xmm6, xmm9
vpermq ymm6, ymm6, 039h
vpermq ymm7, ymm7, 04Eh
;*****[Load M1 values]*******************************
vmovapd ymm0, ymmword ptr [ rcx ]
vmovapd ymm1, ymmword ptr [ rcx + 32 ]
vmovapd ymm2, ymmword ptr [ rcx + 64 ]
vmovapd ymm3, ymmword ptr [ rcx + 96 ]
;*****[Set Mr0c0 = M1r0 * M2c0 ]*********************
vmulpd ymm8, ymm0, ymm4
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr0c1 = M1r0 * M2c1 ]*********************
vmulpd ymm8, ymm0, ymm5
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr0c2 = M1r0 * M2c2 ]*********************
vmulpd ymm8, ymm0, ymm6
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr0c3 = M1r0 * M2c3 ]*********************
vmulpd ymm8, ymm0, ymm7
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Store output row 0]***************************
vpermq ymm9, ymm9, 39h
lea rdx, M
vmovapd ymmword ptr M, ymm9
;*****[Set Mr1c0 = M1r1 * M2c0 ]*********************
vmulpd ymm8, ymm1, ymm4
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr1c1 = M1r1 * M2c1 ]*********************
vmulpd ymm8, ymm1, ymm5
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr1c2 = M1r1 * M2c2 ]*********************
vmulpd ymm8, ymm1, ymm6
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39haddsd xmm9, xmm8
;*****[Set Mr1c3 = M1r1 * M2c3 ]*********************
vmulpd ymm8, ymm1, ymm7
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Store output row 1]***************************
vpermq ymm9, ymm9, 39h
vmovapd ymmword ptr M [ 32 ], ymm9
;*****[Set Mr1c0 = M1r2 * M2c0 ]*********************
vmulpd ymm8, ymm2, ymm4
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr2c1 = M1r2 * M2c1 ]*********************
vmulpd ymm8, ymm2, ymm5
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr2c2 = M1r2 * M2c2 ]*********************
vmulpd ymm8, ymm2, ymm6
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr2c3 = M1r2 * M2c3 ]*********************
vmulpd ymm8, ymm2, ymm7
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Store output row 2]***************************
vpermq ymm9, ymm9, 39h
vmovapd ymmword ptr M [ 64 ], ymm9
;*****[Set Mr3c0 = M1r3 * M2c0 ]*********************
vmulpd ymm8, ymm3, ymm4
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr3c1 = M1r3 * M2c1 ]*********************
vmulpd ymm8, ymm3, ymm5
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr3c2 = M1r3 * M2c2 ]*********************
vmulpd ymm8, ymm3, ymm6
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Set Mr3c3 = M1r3 * M2c3 ]*********************
vmulpd ymm8, ymm3, ymm7
vpermq ymm9, ymm9, 39h
movsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
vpermq ymm8, ymm8, 39h
addsd xmm9, xmm8
;*****[Store output row 3]***************************
vpermq ymm9, ymm9, 39h
vmovapd ymmword ptr M [ 96 ], ymm9
;*****[Set final return]*****************************
lea rax, M
ret
PCC_XMMatrixMultiply endp
