This research activity, originally undertaken in conjunction with an MSc program at the DMU University (UK), was to develop some simple character and shape recognition software using .NET and C#.
The code and results are presented here as an example of how relatively simple C# code can be used to implement the Hopfield Artificial Neural Network to perform character recognition.
Artificial Intelligence techniques, in particular Artificial Neural Networks, are particularly suited to pattern recognition. They compare favorably with other methods of pattern analysis and in some cases they can outperform them. However, they are often computationally expensive.
The Hopfield artificial neural network is an example of an Associative Memory Feedback network that is simple to develop and is very fast at learning. The ability to learn quickly makes the network less computationally expensive than its multilayer counterparts [13]. This makes it ideal for mobile and other embedded devices. In addition, the Hopfield network is simple to develop, and can be built without the need for third party libraries or toolsets thereby making it more attractive for use in mobile and embedded development.
John Hopfield, building on the work of Anderson [2], Kohohen [10] developed a complete mathematical analysis of the recurrent artificial neural network. For this reason, this type of network is generally referred to as the Hopfield network [14].
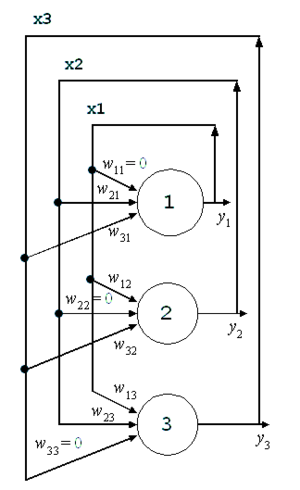
The Hopfield network [8] consists of a single layer of neurons in which each neuron is connected to every other neuron. If the network recognises a pattern, it will return the pattern. However, it suffers the same drawbacks as other single layer networks in that it cannot represent non-linearly separable functions.
The first image shows how the outputs of the network are fed back to the inputs. This means that the outputs are some function of the current inputs and the previous outputs. The result is that an output causes the input to change, causing a corresponding change in output, which in turn changes the input and so on until the network enters a stable state and no further changes take place. The network requires a learning phase but this involves only one matrix calculation, is very short and therefore, computationally inexpensive.
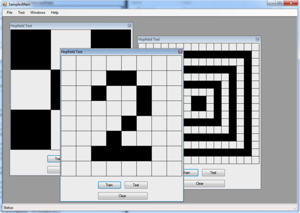
The Hopfield network for this study was implemented using Microsoft C# and Visual Studio 2010. The network and its associated classes were built into a single .NET assembly, whilst the test harness and unit testing utilities were created as separate projects that referenced this library.
The test harness (see screen shot) consisted of a small, graphical user interfaced based program. This test program allowed windows, containing grids of neurons, to be created. Each grid allowed patterns to be entered for training, and for results to be displayed. In addition, the grids allowed for shapes to be drawn using a mouse. The code is available for download here.
The main assembly containing the Hopfield implementation, includes a matrix class that encapsulates matrix data and provides instance and static helper methods. The class implements all common matrix algorithms. Although not universally agreed [13], literature suggests that the neurons in a Hopfield network should be updated in a random order. This has been incorporated into the Hopfield class through the use of a simple, Fisher-Yates, shuffle algorithm.
Results
When testing simple distinct patterns, the network performed well, correctly identifying each pattern. However, as expected, as the patterns increased in similarity, the network often returned incorrect results. These additional states (local minima) dramatically affected the network’s ability to associate an input with the correct pattern.
Hopfield [8] stated that the number of patterns that can be stored was given by the following formula:
P = 0.15n (where P = number of patterns and n = number of neurons)
Based on this, a network of 64 Neurons could store 9.6 patterns. The relationship between the number of neurons and the amount of patterns stored, is not universally agreed, Crisanti et al. [5], suggests a value 8.77 patterns for a 64 neuron network, McEliece et al. [12] and Amari & Maginu [1] suggest 7.11 and 5.82 patterns respectively, for the same network. This suggests that to store and retrieve three patterns, we could need as many as 33 neurons.
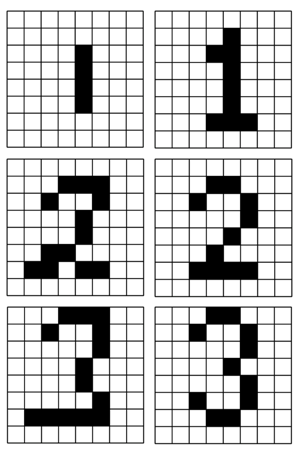
The network was subjectively tested using numeric digits. These tests involved training the network with binary patterns that resembled a numeric digit followed by a testing phase where numeric digits to be tested, were hand drawn using the computers mouse. The Hopfield network correctly identified each number and returned the correct character.
Whilst the experiments did not product a final working character recognition system, they do demonstrate what can be achieved with quite simple code. The code is available for download here.
Enjoy!
References
- [1] Amari, S. & Maginul, K. Statistical neurodynamics of associative memory Neural Networks, 1, 63-74, 1988
- [2] Anderson, J. A. Psych Rev., 84, 413-451, 1977
- [3] Campadelli, P., Mora, P. & Schettini, R. Using Hopfield Networks in the Nominal Color Coding of Classified Images IEEE Universita’ di Milano, 1051-4651/94, 112-116, 1994
- [4] Chen, L., Fan, J. and Chen, Y. A High Speed Modified Hopfield Neural Network and A Design of Character Recognition System IEEE Chung-Yung Christian University, CH3031-2/91/0000-0308, 1991 308-314
- [5] Crisanti, A., Amit, D. & Gutfreund, H. Saturation level of the Hopfield model for neural network Europhysics Letters, 2(4), 337-341, 1986
- [6] Grant, P., & Sage, J. A comparison of neural network and matched filter processing for detecting lines in images Neural Networks for Computing, AIP Conf. Proc. 151, Snowbird, Utah, 194-199, 1986
- [7] Heaton, J. Introduction to Neural Networks St Louis: Heaton Research, Inc, 2008
- [8] Hopfield, J. Neural networks and physical systems with emergent collective computational abilities, Proceedings of the National Academy of Science, USA Biophysics, 79, 2554-2558 , 1982
- [9] Kim, J., Yoon, S., Kim, Y., Park, E., Ntuen, C., Sohn, K. & Alexander, E. An efficient matching algorithm by a hybrid Hopfield network for object recognition IEEE North Carolina A&T State University, 0-7803- 0593-0/92 2888-2892, 1992
- [10] Kohohen, T. Associative Memory-A System Theoretic Approach, New York: Springer, 1977
- [11] Li, M., Qiao, J. & Ruan, X. A Modified Difference Hopfield Neural Network and Its Application Proceedings of the 6th World Congress on Intelligent Control and Automation, June 21-23, 2006
- [12] McEliece, R., Posner, E., Rodemich, E. & Venkatesh, S. The capacity of the hopfield associative memory IEEE Transactions on Information Theory, 33(4), 461-482, 1987
- [13] Picton, P. Neural Networks, 2nd ed. New York: Palgrave, 2000
- [14] Popoviciu, N. & Boncut, M. On the Hopfield algorithm. Foundations and examples General Mathematics 13(2), 3550, 2005
