This is the third in a series of articles demonstrating how to build a .NET AI library from scratch. In this article, we will learn about Perceptron.
Series Introduction
This is the third article of creating .NET library. Below are links for Part 1 & 2:
My objective is to create a simple AI library that covers a couple of advanced AI topics such as Genetic algorithms, ANN, Fuzzy logics and other evolutionary algorithms. The only challenge to complete this series would be having enough time working on code and articles.
Having the code itself might not be the main target however, understanding these algorithms is. Wish it will be useful to someone someday.
Why .NET? When it comes to AI, there are many other languages and platforms that provide pre-ready tools and libraries for different AI algorithms (Python, for instance, could be a good choice, Matlab as well). However, I decided to use .NET where it does not have any AI pre-made libraries by default (as far as I know), hence will have to create all the algorithms from scratch which would give the sense and in-depth view. For me, this is the best way to learn.
Please feel free to comment and ask for any clarifications or hopefully suggest better approaches.
Article Introduction - Part 2 "Perceptron"
In the last article, I reviewed different types of machine learning types as part of AI composition. Training is one aspect, what about "Intelligence" component itself?
Well, researchers from early AI days focused to mimic human intelligence into machines/applications. The early formation was Perceptron which mimics the smallest processing unit in human central nervous system.
Using brain anatomy, nervous system at its core consists of large number of highly interconnected neurons that work in both ways, Sensory (inputs) and Motor (actions as muscles).
Here are a couple of resources which provide introduction to neural networks:
What is Perceptron?
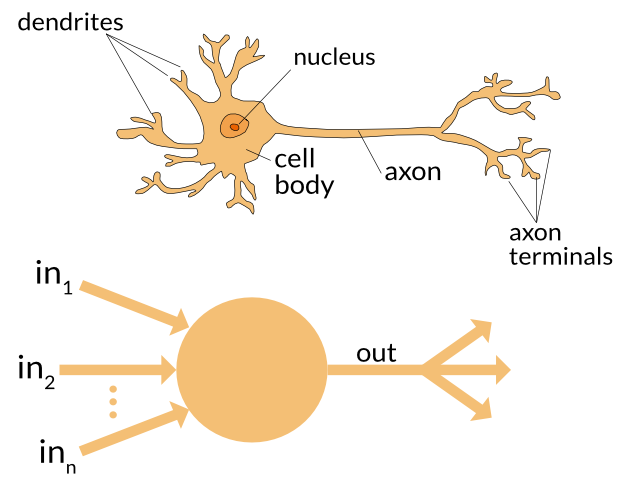
You may consider Perceptron as the smallest processing element which mimics a single neuron:

Electrically speaking, Perceptron receives input(s), does some processing and then produces output. At biological origin, neuron receives sensory information via dendrites in the form of chemical/electrical excite or inhibit actions, the summation of all actions are then transferred to axon within the same chemical/electrical form.
Axon terminals convert the axon electrical signal into excite or inhibit signal based on threshold value.
Same can be converted to electrical terms where Perceptron sum all its inputs and generates output. To mimic axon terminals, we need some kind of conversion function to convert summation into excite or inhibit. This conversion function is called Activation or Transfer function in ANN terminology.

Above is a very simple mimic which has a major flaw, there is no room for intelligence, output is directly derived from inputs and that is it. Besides that, all inputs are equally treated which might not be always the case; some inputs may have higher priority than others.
To overcome this flaw, let's introduce Weights to inputs so each input shall has its own weight. In such a case, manipulating weights could yield different output value even with same inputs set.

So, what are the values of weights? Clearly, neural network is a mapping function between output to inputs. In other words, ANN is an optimization function. Setting weights (other way to name it is, Perceptron training) is the way to use to impose AI into Perceptron.
The following algorithm represents Perceptron Training:
How to update Weights? Let's assume we have only 1 input X and Desired output (label) Y, then:
h(x) = X * W
Applying Gradient Descent algorithm from the last article, for <code>b</code> parameter:

b in our case is W, m=1 then:

Where r is the learning rate to control step, normally 0 < r < 1.
What is termination condition? Iteration could terminate once the iteration error is less than a user-specified error threshold or a predefined number of iterations have been completed.
Let's revisit our algorithm:
For the record, the above Perceptron layout and training algorithm is known as McCulloch and Pitts model (MCP)
What is Activation Function?
As discussed, activation function or transfer function used to convert Perceptron output to excite or inhibit. For example, let's assume we are using Perceptron to detect +ve numbers from a set of numbers.
In this case, activation function shall be simply a step function:

So, activation function to use depends on application or problem being solved.
Here are a couple of commonly used activation functions:

* Source: Wikipedia article
When to Use Perceptron?
Clearly, Perceptron provide basic processing function in the form of:

Consider a case of 1 input, then graph of h(x) shall be similar to:

as a straight line, it can segregate 2 regions, let's say group A and group B:

This is a Linear Classifier or Binary Classifier function. If you would recall, classification was the second type of supervised learning. Perceptron is used in binary classification type of problems where we have only two possible solutions or groups for each input set.
Nonlinear classifier function could be something as below:

In such case, Perceptron cannot be used and other algorithms shall be applied (for later discussion).
As a recap, Perceptron can be used only to answer questions as "Does this set of inputs fit in group A or group B?" given that A & B are linearly separated.
Full Linear Perceptron
Consider the above example of 1 input x and h(x) = X * W for groups A & B.
Let's assume we do have other 2 groups, C & D, which are linearly separated as per the following:

Current Perceptron cannot be used to optimize the above function where, regardless the value of W; output will be always 0 incase input is 0 which does not represent the above graph.
To resolve this issue, we have to build full linear Perceptron h(x) = a + X * W
How to define a? To simply Perceptron design and training as well, AI community agreed to include a Bias concept into Perceptron by assuming that there is always input X<sub>0 </sub>=1 hence a shall be the weight for this input, so:

X0 = 1:

Accordingly, final Perceptron design shall be:

Sample Code
Perceptron Class
To create a Perceptron Class, the following are minimal fields:
Private _Size As Integer
Private _Weights As Matrix1D
Private _LearnRate As Single
Constructor
Accepts size of Perceptron (number of inputs including bias) and learning rate:
Public Sub New(PerceptronSize As Integer, LRate As Single)
Me._Size = PerceptronSize
Me._Weights = New Matrix1D(Me.Size)
Me._Weights.RandomizeValues(-100, 100)
Me._LearnRate = LRate
End Sub
Hypothesis Function, calculates h(x)=∑(Xi * Wi) and returns h(x) as matrix:
Public Function HypothesisFunction(Input As Matrix1D) As Matrix1D
If Input.Size <> Me.Size Then Throw New Exception_
("Input Matrix size shall match " & Me.Size.ToString)
Dim HypothesisFun As New Matrix1D(Me.Size)
HypothesisFun = Input.Product(Weights)
Return HypothesisFun
End Function
CalcOutput calculates final output of activation function:
Public Function CalcOutput(Input As Matrix1D, _
ActivationFunction As IActivationFunction) As Single
Dim Hypothesis_x As Single = Me.HypothesisFunction(Input).Sum
Return ActivationFunction.Function(Hypothesis_x)
End Function
TrainPerceptron, is the main training function. It accepts 2 arrays; one is training set inputs matrices and other is labels array (correct answers):
Public Sub TrainPerceptron(Input() As Matrix1D, Label() As Single, _
ActivationFunction As IActivationFunction)
Dim m As Integer = Input.Count
Dim Counter As Integer = 0
Dim MSE As Single = 0
Dim IterateError As Single = 0
Do
Counter += 1
MSE = 0
For I As Integer = 0 To m - 1
Dim Out As Single = Me.CalcOutput(Input(I), ActivationFunction)
IterateError = Out - Label(I)
For Index As Integer = 0 To Me.Size - 1
Me._Weights.Values(Index) = Me._Weights.Values(Index) - _
Me.LearnRate * IterateError * Input(I).GetValue(Index)
Next
MSE += IterateError
IterateError = 0
Next
MSE = 1 / (2 * m) * MSE * MSE
Loop Until MSE < 0.001 OrElse Counter > 10000
End Sub
Simply, it iterates in all training set inputs and update weights in each iteration. Then repeats the same steps till loop is terminated.
Loop shall be terminated if MSE reached a value below 0.001 and in some cases (mostly if inputs are not linearly separated) need to have a safety condition to avoid infinite loops, hence max number of iterations (tracked by variable Counter) is set to 10,000.
Activation Functions
To simplify implementation of different activation functions, an interface IActivation has been created:
Namespace ActivationFunction
Public Interface IActivationFunction
Function [Function](x As Single) As Single
Function Derivative(x As Single) As Single
End Interface
End Namespace
Each activation function shall implement 2 methods, Function and Derivative (this is for later use).
The following activation functions have been implemented:
IdentityFunction

Namespace ActivationFunction
Public Class IdentityFunction
Implements IActivationFunction
Public Function [Function](x As Single) _
As Single Implements IActivationFunction.Function
Return x
End Function
Public Function Derivative(x As Single) _
As Single Implements IActivationFunction.Drivative
Return 1
End Function
End Class
End Namespace
ReluFunction

Namespace ActivationFunction
Public Class ReluFunction
Implements IActivationFunction
Public Function [Function](x As Single) _
As Single Implements IActivationFunction.Function
Return Math.Max(x, 0)
End Function
Public Function Derivative(x As Single) _
As Single Implements IActivationFunction.Drivative
If x >= 0 Then Return 1
Return 0
End Function
End Class
End Namespace
SignFunction
Namespace ActivationFunction
Public Class SignFunction
Implements IActivationFunction
Public Function [Function](x As Single) _
As Single Implements IActivationFunction.Function
If x >= 0 Then
Return 1
Else
Return -1
End If
End Function
Public Function Derivative(x As Single) _
As Single Implements IActivationFunction.Drivative
Return 0
End Function
End Class
End Namespace
SoftStepFunction or Logistics Function

Namespace ActivationFunction
Public Class SoftStepFunction
Implements IActivationFunction
Public Function [Function](x As Single) As Single _
Implements IActivationFunction.Function
Dim Y As Single
Y = Math.Exp(-x)
Y = Y + 1
Y = 1 / Y
Return Y
End Function
Public Function Derivative(x As Single) As Single _
Implements IActivationFunction.Drivative
Dim Y As Single
Y = [Function](x)
Return Y * (1 - Y)
End Function
End Class
End Namespace
StepFunction

Namespace ActivationFunction
Public Class StepFunction
Implements IActivationFunction
Public Function [Function](x As Single) As Single _
Implements IActivationFunction.Function
If x >= 0 Then
Return 1
Else
Return 0
End If
End Function
Public Function [Function](x As Single, Theta As Single) As Single
If x >= Theta Then
Return 1
Else
Return 0
End If
End Function
Public Function Derivative(x As Single) As Single _
Implements IActivationFunction.Drivative
Return [Function](x)
End Function
End Class
End Namespace
Sample Test

GUI

Sample application creates random training set with pre-defined relation and passes this data to Perceptron for training, then draws classification line based on final Perceptron weights.
TrainingSet Class
Public Class TrainingSet
Private _PointsNum As Integer
Private _Width As Integer
Private _Height As Integer
Private _Points() As Matrix1D
Private _Labels() As Single
Private _Gen As RandomFactory
Public Sub New(PointsNum As Integer, Width As Integer, Height As Integer)
_PointsNum = PointsNum
_Width = Width
_Height = Height
_Gen = New RandomFactory
ReDim _Points(PointsNum - 1)
ReDim _Labels(PointsNum - 1)
Randomize()
End Sub
Public Sub Randomize()
For I As Integer = 0 To _PointsNum - 1
Points(I) = New Matrix1D(3)
Points(I).SetValue(0, 1)
Points(I).SetValue(1, _Gen.GetRandomInt(0, _Width))
Points(I).SetValue(2, _Gen.GetRandomInt(0, _Height))
Labels(I) = Classify(Points(I).GetValue(1), Points(I).GetValue(2))
Next
End Sub
Public ReadOnly Property Points As Matrix1D()
Get
Return _Points
End Get
End Property
Public ReadOnly Property Labels As Single()
Get
Return _Labels
End Get
End Property
Private Function Classify(X As Single, Y As Single) As Single
Dim d As Single = 300 - 2 / 3 * X
If Y >= d Then Return +1
Return -1
End Function
Public Sub Draw(MyCanv As Canvas)
For I As Integer = 0 To _PointsNum - 1
If _Labels(I) = 1 Then
MyCanv.DrawBox(5, Points(I).GetValue(1), _
Points(I).GetValue(2), Color.Blue)
Else
MyCanv.DrawCircle(5, Points(I).GetValue(1), _
Points(I).GetValue(2), Color.Green)
End If
Next
End Sub
End Class
Creation of Perceptron and TrainingSet:
Private Sub SampleTest1_Load(sender As Object, e As EventArgs) Handles MyBase.Load
RndTraininSet = New TrainingSet(100, PictureBox1.Width, PictureBox1.Height)
MyCanvas = New Canvas(PictureBox1.Width, PictureBox1.Height)
MyPerceptron = New Perceptron(3, 0.1)
ActivFun = New SignFunction
End Sub
One important note here is Activation function selection, as mentioned, activation function selection is dependent on problem being resolved. For our example, training set is divided into two groups, +ve and -ve based on point location from defined straight line.
Based on this problem criteria, the best activation function is SignFunction which outputs +1 or -1.
Try changing to other functions, for some; Perceptron will never reach min MSE state.
Perceptron Training
Private Sub btnTrain_Click(sender As Object, e As EventArgs) Handles btnTrain.Click
MyPerceptron.TrainPerceptron(RndTraininSet.Points, RndTraininSet.Labels, ActivFun)
End Sub
Recap
Perceptron is the basic processing node in ANN (Artificial Neural Network) which is used mainly to resolve Binary Linear Classification problems.
Perceptron uses Supervised learning to set its weights.
Formula to update weights in each iteration of training set is:

Activation function defines the final output of Perceptron and selection of activation function is based on problem being resolved.
History
- 16th September, 2017: Initial version
