Multiple Precision Arithmetic: Sum Algorithm

This article is part of a series of articles:

Multiple Precision Arithmetic: A recreational project

• Part #1, The Sum
• Part #2, The Subtraction
• Part #3, The Multiplication
• Part #4, The Division
• Part #5, Using the Code
• Github Repo

Introduction

A computer operates on numeric values up to a given size. At the time of writing, 64 bit arithmetic can be found on cheap hardware. But there's a fixed limit, if you need to operate above that limit, you must use an algorithm to instruct your computer how to do, it is not “out of the box”.

On this series, I will share my knowledge and also some code. My goal is to write a minimal collection of working arithmetic algorithms and share them with as many fellow programmers as possible. It is not my objective to create a serious library, outstanding MP libraries for many languages exist written by professional mathematicians out there.

The series is divided into four background articles, then the last article will explain how to use my code just in case you want to challenge my "reference" implementation of the simple arithmetic operations.

A real MP library will need to implement a lot more, will handle negative numbers and fractions, polynomials, here I will cover the basic four arithmetic operations.

Long Numbers

To communicate a concept like "there're 12334 stones in that pot" without using Arabic numerals could be hard. Well it's hard using Arabic numerals too, but at least you get an idea of the order of magnitude of number of stones in a pot, better than communicate the concept by sending a picture of stones laid on a table, at least that's my opinion, this is why Arabic numbers are a superior tool; how great were those ancient mathematicians who discovered lot of mathematics without having Arabic numbers.

By the way, without having to dig too much into positional notation, we can observe that "12334" is not a number, it is a string of digits which represent a number in a very compact form, easier to handle for the brain than the picture of 12334 stones laid on a table. We can use that string to compare numbers, and to do arithmetic in a simpler way than using a bunch of stones (stones translate to calculi in ancient-romans-Latin words).

We learned at least four algorithms in our childhood to work on long numbers: long sum, long subtraction, long multiplication and long division, better algorithms do exists but we will start with them.

A Short Note

In this series, I will only focus on UNSIGNED arithmetics.

Background

The sum is one of the basic arithmetic operations. To sum a pair of numbers, you only need to know how to count. To sum 23+98 means to count 98 after 23. But when you have to calculate 100 000 + 133 212 you better use  positional decimal notation and an algorithm that requires to count up to 10 (on base 10). We’ll call such algorithm the Long Sum Algorithm, we will use it because it requires less effort than counting.

We will now define a primitive operation, then we'll build the long sum algorithm.

Simple Sum Base 10 (Our Primitive Operation)

Let me define a name for the sum of numbers A and B, where A and B have 1 digit (where digit can have any base, eg: 10, 16, 64, 2³²): I'll call it simple sum, in base 10, you can compute it by counting up to 9.

Example 1:

3+3 = starting from first number after 3 (it’s 4) keep counting for 3 times: 4,5,6: so, the result is 6

Example 2: (what happens if the result requires more than 1 digit?)

Overflow

8 + 4 = starting from 9 keep counting for 4 times:  9, 10 (overflow: mark on paper that you have carry and continue counting from 1), 1, 2; so, the result is 2 and you have carry, the carry, if present, is always 1.

Some Interesting Properties of the Simple Sum

Regardless of the base b (e.g..: 10), if A + B >= b then:

• we have carry
• the result has 2 significant digits
• the most significant digit being 1
• the least significant digit is less than any of the operands, in other words, if A+B >= b, then result is two digit [1][R] where R<A and R<B (Appendix A1 if you need a proof).

And symmetrically if A + B < b then:

• we don’t have carry
• the result have 1 digit
• that digit will always be greater than or equal to any of the operands (Appendix A1)

Corollaries

• The result of a long sum has 0 or 1 digit more than the longest addend (facilitate allocation of space for the result).
• The leftmost allocated digit which holds the result, will always be 1 or 0 even when you sum 1 to the 2 digits result of a simple sum (means that you can always add carry from the previous operation without having to allocate new digits), let me explain better:
  • We said that carry for A+B+1 is 0 for sure if A+B already had carry. For example: 9 is the greatest single digit number in base 10, if we sum 9+9 we get
    • 9+9 = 18,
    • we had overflow, thus most significant digit is 1
    • least significant digit is 8
    • you can safely add 1 to 8 without needing to have another overflow, thus leftmost can never be 2.

Caution: 4+5=9 if you add 1 you get a carry there, but the result is still 2 digits, having [1] to the left, that means that you may need to propagate the carry toward left, that makes it difficult to parallelize the sum algorithm.

• Important: If the lowest significant digit is less than any of the operands, then we have carry: if we sum single digits [A] + [B], the result is going to be [carry?] [R], we can infer the value of carry with the following expression:
  • if R<A (R<B works too) then
          carry = 1
    else
           carry = 0.

That means we can ignore the hardware carry flag, we can infer the carry comparing the lower digit of the result to any of the operands.

Long Sum in Base 10

To sum numbers with more than 1 digit, we’ll apply a long sum algorithm.

I’m going to use the algorithm we learned at age of 6, to implement Long Sum on the CPU.

That is a serial algorithm, I think it is possible to tweak the above interesting properties to create a parallel algorithm to be used on SIMD hardware such as MMX on x64 CPUs or multi core GPUs, but that should be a new article, if I’ll ever go for it.

CPU Register Digit to Decimal Digit Analogy

To proceed further, we need to get the analogy between a decimal digit and a CPU register digit alias CPU word. From our point of view, a 64 bit word is no different than a decimal digit.

The long sum algorithm is the same for children and computers, the difference is only in the size of digits and the primitive simple sum used, which is counting up to ten for us humans, using the CPU builtin sum instruction for the software implementation.

Long Sum at the Digital Computer (the same as base 10 but using base 2^{integer_register_size})

The CPU can sum register sized digits (words). A modern CPU can sum 32/64/… bits with 1 clock cycle throughput. Our approach is to use register size digits and the CPU carry flag, or carry detection algorithm, instead.  

The Algorithm

The algorithm here proposed is a high level overview of the actual algorithm, the idea is to split the long sum of A+B into a sequence of simple sums A_n+B_n, starting with the least significant digits of both numbers, we also have to propagate carry at each iteration. Possible optimizations are just plain ignored.

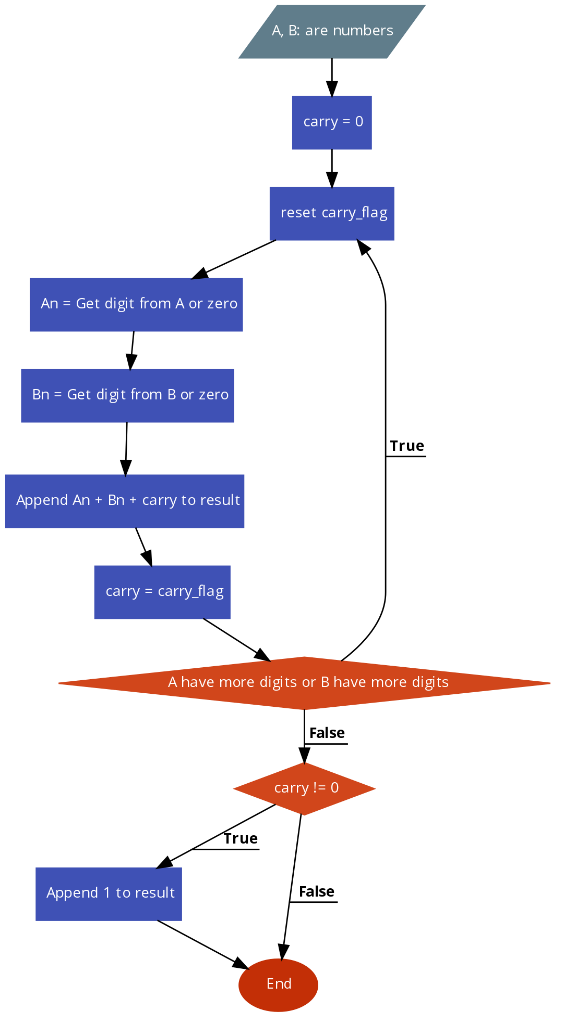
Carry Detection Variants

The above algorithm has a sub algorithm at point carry = carry flag, here we detect the carry from previous simple sum.

CPUs have hardware to detect and bit flag to indicate carry.

That CPU flag is generally not available to higher level languages, but carry can be obtained by using the property we discussed a little earlier.

There are four ways that I know to detect carry.

1. Use the hardware carry flag.
2. Use the property that (when doing An+Bn) carry is 1 if and only if (R < An or  R < Bn) , this is tricky because we are no longer talking about R = An+Bn, we are talking about R = An+Bn+previous_carry. So the actual test is going to be: carry_flag = if(previous_carry = 1) (R <= An ? 1 : 0), else if(previous_carry=0) (R < An) ? 1 : 0, or by doing: carry_flag = (R < An || R < Bn) ? 1 : 0) that option tends to be the most portable and it is my preferred way of dealing with the carry, but performance-wise, we should measure both sub-variants. A hacky method, if the compiler supports it, to avoid branching could be: carry_flag = (R < An | R < Bn); that should work if the compiler produces expected code, unit tests (or look at disassembled code) can tell you if the generated code is actually working.
3. Use a number system where you reserve the highest bit instead of the carry (e.g.: on 32 bits CPU, represent numbers as strings of 31 bits, which may also be useful if language does not provide unsigned types) but that's useless complication.
4. If the high level language offers an integer type that is at least 1 bit larger than the register size, we can use this type to store R, the higher level language will automatically move the carry flag into the lowest bit of the higher word, I give two examples in C language of using that third variant:
   C++

   /*
   First Example: Using union
   Using a UNION to avoid bitwise ops: we must pay attention 
   to do right casts and to the endianness of the target hardware
   */
   
   #include <stdio.h>
   /* this is not the complete algorithm, we are only showing the
   carry detection part in the evidenced lines
   
   suppose that word_t corresponds to the hardware CPU register_size  and
   that dword_t corresponds to 2 times the register_size, NOTE THAT
   we just need a type having 1 bit more than the register_size for sum,
   but later on we might need 2 times the register_size to do multiplications
   */
   typedef
   union _reg_long {
       dword_t DW;
   
       struct _reg_words
       {    /*on big endian field order should be inverted I guess*/
           word_t Lower;
           word_t Higher;
       } words;
   } reg_long;
   
   int main()
   {    
       reg_log rl;
       word_t R;
       short prev_carry = 1;
       short carry;
       word_t An = ((word_t)-1);
       word_t Bn = 0;
       
       rl.DW = (dword_t)An + Bn + prev_carry;
       carry = rl.words.Higher;
       R = rl.words.Lower;
   
       printf("New carry: %d, Result:%x", carry, R);
       return 0;
   }
   
   /*
   Second Example: Using bitwise ops
   template for languages not having union types, but have some bitwise operations
   */
       
   dword_t rl;
   word_t R;
   short prev_carry = 1;
   short carry;
   word_t An = ((word_t)-1);
   word_t Bn = 0;
   
   rl = (dword_t)An + Bn + prev_carry;
   carry = rl >> (8*sizeof(word_t)) ;
   R = rl & ((word_t)-1);
   
   printf("New carry: %d, Result:%x", carry, R);

Using Understanding the Code

For completeness, I am going to provide a C implementation of the algorithm, note how overflow (carry) can be detected when using high level languages without having to use carry flag. Interface is coarse, the idea is to have a primitive to construct more complex stuff; it needs to be as fast as possible so does not waste time on input checking or create nice data structures, that's not the responsibility of the primitive function. This may be wrapped by other code to generate a cleaner interface:

/*
Preconditions: Will not check array bounds on R, thus R must have space 
to accommodate MAX(ASIZE, BSIZE)+1 unsigned reg_t.
This implementation requires the least significant digit is at index 0,
I did not optimize to keep code clear, but consider that second and third loop could be
divided into 2 loops: after the first time carry becomes zero 
it will never be 1 again, thus we could eliminate the carry detection 
and just memcpy the remaining bits of A into result.
*/

typedef unsigned long long reg_t;

reg_t LongSum(reg_t* A, reg_t ASize, reg_t * B, reg_t BSize, reg_t* R)
{
    reg_t carry;
    reg_t i;
    reg_t min_a_b = ASize > BSize ? BSize : ASize;

    carry = i = 0;

    while (min_a_b > i)
    {        
        R[i] = A[i] + B[i] + carry;
        carry = R[i] < A[i] + carry ? 1 : 0;
        ++i;
    }

    while (ASize > i)
    {        
        R[i] = A[i] + carry;
        carry = R[i] == 0 ? 1 : 0;
        ++i;
    }

    while (BSize > i)
    {    
        R[i] = B[i] + carry;
        carry = R[i] == 0 ? 1 : 0;
        ++i;
    }

    if (carry)
        R[i] = 1;

    return i;
}

The slightly optimized “reference” version:

/*  Will not check array bounds on R, thus must have space to 
    accommodate MAX(ASIZE,BSIZE)+1 unsigned ints
    returns length of Result
*/
numsize_t LongSumWithCarryDetection
(reg_t* A, numsize_t ASize, reg_t * B, numsize_t BSize, reg_t* R)
{
    register reg_t carry;
    register numsize_t i;
    reg_t min_a_b = ASize > BSize ? BSize : ASize;

    carry = i = 0;

    while (min_a_b > i)
    {        
        R[i] = A[i] + B[i] + carry;
        carry = R[i] < A[i] + carry ? _R(1) : _R(0);
        ++i;
    }

    while (ASize > i && carry == 1)
    {        
        R[i] = A[i] + carry;
        carry = R[i] == _R(0) ? _R(1) : _R(0);
        ++i;
    }

    while (ASize > i) /*just copy words*/
    {
        R[i] = A[i];
        ++i;
    }

    while (BSize > i && carry == 1)
    {    
        R[i] = B[i] + carry;
        carry = R[i] == _R(0) ? _R(1) : _R(0);
        ++i;
    }

    while (BSize > i)
    {
        R[i] = B[i];        
        ++i;
    }

    if (carry)
    {
        R[i] = _R(1);
        ++i;
    }

    return  (numsize_t)i;
}

I also attempted to do the same in Assembly x64, I am not good at assembler, but here’s my x64 code:

.data

.code
    ;int LongSumAsm(
    ;     qword  * A,         RCX
    ;     int ASizeInQWords,     RDX
    ;     qword * B,             R8
    ;     int BSizeInQWords,     R9
    ;     qword * R            ON STACK
    ; );            
; RAX, RCX, RDX, R8, R9, R10, R11  VOLATILE
; RAX used to store cpu flags
LongSumAsm proc
    
    ;stack frame
    push rbp
    mov rbp, rsp
    push rbx                ;rbx is non volatile...
    
    
    ; the following three instructions move the minimum of ASize, BSize into R9    
    mov r11, rdx               ; suppose minimum is ASize, thus Asize in R11
    cmp rdx, r9                ; compare ASize, BSize
    
    mov [rbp + 20o], rdx       ;ASize in [rbp + 20o] that is second qword in shadow space
    mov [rbp + 30o], r9        ;BSize in [rbp + 30o] that is third qword in shadow space    
    
    cmova r11, r9              ; if ASize > BSize , move BSize into R11
    
    
    clc    ;clear carry
    lahf   ;load flags in ah

    ; use shadow stack space to save inputs
        
    mov r10, qword ptr [rbp + 60o]            ; keep R in R10, R is in stack at rbp + 60o
    
    xor r9, r9                                ; zero in r9, from now on r9 will be 
                                              ; the index on the arrays
    
    lea r11, [r11*8]
    
    A_And_B_Loop:                             ; while (ASize > i && BSize > i)                
        cmp r11, r9                           ; compare MinSize (r11) 
                                              ; and array index (r9)
        jle A_And_B_Loop_Ends                 ; if index >= minsize quit loop
        mov rbx, qword ptr [rcx + r9]         ; A[index] in rbx
        mov rdx, qword ptr [r8 + r9]          ; B[index] in r11
        sahf                                  ; reload flags from rax
        adc rbx, rdx                          ; add with carry A[index] + B[index]
        
        lahf                                  ; store flags into rax
        mov qword ptr [r10+ r9], rbx          ; save to R[index] 
                                              ; the result of A[index] + b[index]
        
        add r9, 8                             ; increase index
        jmp A_And_B_Loop                      ; continue loop
        
    A_And_B_Loop_Ends:
    
    xor r11, r11                              ; zero into r11    
    mov rdx, [rbp + 20o]                      ; rdx = size A
    lea rdx, [rdx*8]
    A_Only_Loop:                              ; while (ASize > index)      
        cmp rdx, r9                           ; compare ASize (rdx) and array index
        jle A_Only_Loop_Ends                  ; if(index <= ASize) quit loop
        mov rbx, qword ptr [rcx + r9]         ; A[index] into rbx
        sahf                                  ; reload flags from rax into flags register
        adc rbx, 0                            ; add with carry A[index] + 0 (0 in r11)        
        lahf                                  ; store flags into rax
        jnc A_NoCarry_Loop                    ; carry is zero no need to 
                                              ; do more additions
        mov qword ptr [r10 + r9 ], rbx        ; save to R[index]    
                                              ; the result that's in rbx
        add r9,8                              ; increase index
        jmp A_Only_Loop                       ; continue loop

    A_NoCarry_Loop:
        mov qword ptr [r10+ r9], rbx          ; save to R[index] 
                                              ; the result of A[index] + b[index]
        add r9, 8                             ; increase index
        cmp rdx, r9                           ; compare MinSize (rdx) 
                                              ; and array index (r9)        
        mov rbx, qword ptr [rcx + r9]         ; A[index] into rbx
        jle A_Only_Loop_Ends                  ; if index >= minsize quit loop
        jmp A_NoCarry_Loop                    ; continue loop
    
    A_Only_Loop_Ends:
    
    mov rdx, [rbp + 30o]                      ; move BSize into rdx
    lea rdx, [rdx*8]
    B_Only_Loop:                              ; while (BSize > index)
        cmp rdx, r9                           ; compare BSize (rdx) with array index
        jle B_Only_Loop_Ends                  ; if index <= BSize quit loop        
        mov rbx, qword ptr [r8 + r9]          ; B[index] into rbx                
        sahf                                  ; reload carry flag into flag registers
        adc rbx, r11                          ; add with carry B[index] + 0 (0 in r11)        
        lahf                                  ; store flags into rax
        jnc B_NoCarry_Loop                    ; carry is zero no need to 
                                              ; do more additions
        mov qword ptr [r10 + r9], rbx         ; save to R[index] 
                                              ; the result that's in rbx    
        add r9, 8i                            ; increase index
        jmp B_Only_Loop                       ; continue loop

    B_NoCarry_Loop:
        mov qword ptr [r10+ r9], rbx          ; save to R[index] the result of B[index]
        add r9, 8i                            ; increase index
        cmp rdx, r9                           ; compare BSIze (rdx) and array index (r9)
        jle B_Only_Loop_Ends                  ; if index >= BSIZE quit loop
        mov rbx, qword ptr [r8 + r9]          ; rbx into result
        jmp B_NoCarry_Loop                    ; continue loop

    B_Only_Loop_Ends:
    
    sahf                                      ; reload flags into flag registers
    jnc Prepare_to_return
    mov r11, 1                                ; add with carry 0 + 0 (last carry in r11)    
    mov qword ptr[r10 + r9], r11              ; store the last carry flag into R[index]
    add r9, 8

    ; return value
    Prepare_to_return:
    mov rax, r9
    shr rax, 3

    ; resume stack frame
    
    pop rbx
    mov rsp, rbp
    pop rbp
ret
LongSumAsm endp
end 

Aftermath

Here is some speed comparison of assembly x64 vs C second “reference” version, my CPU is a 2011 quad core i7 3Ghz

C version compiled in release mode seems to be quite good, in sum of small vs big numbers is faster than assembly, but all other tests ASM is faster than C: numbers must be taken with a grain of salt because I am not sure I have everything under control here nor that the C algorithm is exactly the same as assembler because I wrote assembler from scratch not translating C code:

ASM 50% faster than C here (0,0125 secs vs 0,018 secs) VC++2019 on i7(2011)

But changed compiler (VC++2022) and computer (i9 2021), and now ASM slower than C on same test:

Here, they are almost equals, (0,64 seconds ASM vs 0,56 seconds C) but C version looks good on small number vs big one.

VC++2019 on i7(2011)

Same test on VC++2022 on i9(2021), the difference is even smaller, they are at par, no picture but... trust me.

Last test here below, this is serious because now we sum 2 very large numbers (33 million bits each).

This test ASM version is 4 times faster than C (VC++2019, i7 2011), maybe I forgot to start optimizer before that run, I no longer have that CPU so... I'll never know.

Same test on VC++2022, (i9 2021), huge improvement of the C version due to new compiler leveraging newer CPU.

Points of Interest

Some things are worth noting, ASM language seems to be faster when using hardware instruction which is not available in higher level languages such as C. These advantages are difficult to measure, because the C compiler is usually smart in creating machine code that tweaks CPU out of order execution and stuff. For arbitrary long numbers when long sum/sub/mu/div are involved, ASM is superior to C, but the interesting thing to note is that C is not that bad, it's quite good, I'd say that with new vc2022, the compiler is faster than ASM considering the fact that I am guessing the carry and not using the hardware carry flag.

The second thing to note is that I think a good C compiler, for a given platform, could provide a library of function that maps to hardware instructions (intrinsic), so can expose to developer the same hardware as ASM and, if the compiler is smart, that's enough to beat most of handwritten ASM implementation, in particular, if the ASM implementor is me.

Appendix A1

If we have an overflow in A+B, (A and B are single digits) in any base b, Result will be less than any of the operands

Doing the simple sum of A+B we obtain two digits result: Result (the least significant digit) and Carry (carry can only be equal to 1 or equal to 0 and it’s the most significant digit).

We want to show that when \(A+B \geq b\) then the least significant digit is less than both A and B, we can say it in other words as:

The intuitive idea to demonstrate the right arrow is that, if we start to count from \(A\) for \(B\) times, as we reach \(b\), we have consumed at least 1 unit of \(B\), so \(B\) will be greater than \(Result\), and the same for \(A\), vice versa if A + B <b we move units from A to B without restart counting from 0, then result will be greater than both.

My intuitive idea for the left arrow is to think of digits as two buckets capable of contain b-1 water molecules, if you want to pour in the b^th molecule into a digit, but the digit is full, you must empty the bucket, and the remaining molecule must be added to the bucket on his left. So with that metaphor, try to think what happens to bucket Result , which is initially empty, as you pour in A molecules + B molecules, since Result has not been emptied (because it can contain all the molecules in A and B) then the water level on Result is higher than the level on A and B.

Ok, let's give a rigorous proof for the right arrow, I will produce the left arrow demonstration if asked.

I start by showing the following equality

As you may argue by just looking at the above expression the equality is true, now we'll reorder things a bit:

Ok, (2) is exactly telling us that, when \( A + B > b \) then the result is 2 digit long, we can rewrite (2) to evidence its positional notation as

Note that the gray part of (3) \(\color{gray}{B + A - b} \geq 0\), because the hypothesis was \(B + A \geq b\), but we also want it to be less than b, otherwise it will not fit into a single digit.

So we want \(\color{gray}{B + A - b}< b\) (in other words, we want \(\color{gray}{B + A - b}\) to fit into a single digit); let me show that \(0 \leq \color{gray}{B + A - b} < b\)

Let's again rewrite A and B as the difference on b

that's correct, now the grayed part is a positive number (because both \(A\) and \(B\) are single digits, thus they live in the integer interval \([0, b-1]\)) ... in simple words  \(0 < i \leq b\) and that \(0 < j \leq b\)

but we need also that \(i + j \leq b \), luckily that is true because

Ok, now the fact that all those three expressions are true \(0 < i \leq b\) and that \(0 < j  \leq b\) and that \( i + j \leq b \) is equivalent to

By using (11), next we will show that

let's do it by substituting A and B with (b-j) and (b-i)

Being (11) true, then (16) is also true, and thus we unveiled that (12) is true

Ok, let's resume from the equation (3)

\(\color{gray}{(B + A - b)}\)is the least significant digit of \(A + B\), while \(1\) is the most significant: we'd relabel the most significant digit as \(carry\) (we also know its value is always \(1\) now), then we label \(\color{gray}{(B + A - b)}\) as \(Result\).

Originally, we wanted to show that \(Result\) is less than both \(A\) and \(B\), when the hypothesis stands true (the hypothesis were that \(A + B \geq b\)).

To proof thesis, it suffices to show that (17) \(B + A - b < A\) and that (18) \(B + A - b < B\), the method is the same, let's see the case (18) \(B + A - b < B\)

Since \(b > A\), by definition of a digit, we can then say that \(A - b < 0\)

So the expression (18) is true, because \(A - b < 0 \) quod erat demostrandum

Now we must show that (17) \(B + A - b < A\), just let me reorder it \(A + B - b < B\)

\(b - B\), by definition of a digit, we can then say that \(B - b < 0\)

So the expression (17) \(B + A - b < A\) is true, because \(B - b < 0\) quod erat demostrandum

History

• 2017: Started writing
• 4^th February, 2019: Almost ready to publish
• 11^th June, 2022: Published online