Not Levenshtein

• Download AffinityTester.zip - 98 KB

Introduction

Lastly, I had to read in service-reports, and map occurring technical terms to database-known terms (for billing purposes, if you want to know it in detail).
I built an application to choose a "reference-string" (from the service-report), and get a huge range of "hypotheses" from the database - ranked by similarity to the reference.
I was disappointed, how bad the levenshtein-algorithm did the ranking-job.

Fortunately, in the night, I got an inspiration, how to define text-similarity in a complete different way - I named it "TextAffinity".

For demonstration, here I re-built the abovementioned application, using about 2000 song-titles as hypotheses-data (instead of technical terms).
See some results:

  

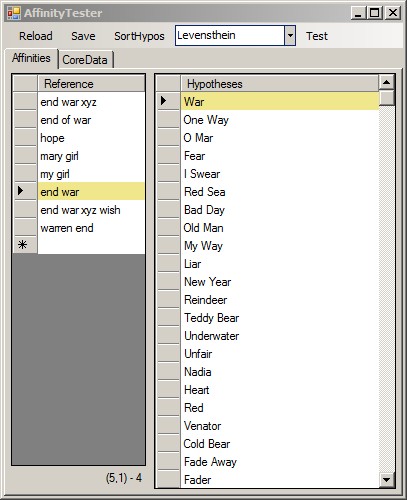
On the left, see the Levenshtein-result: only one of the Hypotheses seems to be related to the queried reference at all! (in human understanding).
While TextAffinity on the right brings up (all of the) 21 Hypotheses of the database, which contain a matching word.

What's Wrong with Levenshtein?

Levenshtein postulates a small set of atomic char-operations (insert, replace, delete), and computes, how to apply them with minimal step-count, to convert a hypothesis to a reference-string,
There are several codeproject-tips about - different implementations - I recommend this one, since its graphical presentation eases to understand the (real tricky!) algorithm.

But applying atomic operations on chars is not, how a human brain usually recognize texts as "similar".
Humans observe groups of matching chars - especially words (a char-group between spaces).

TextAffinity - Definition of Concept, and an Implementation

TextAffinity sees matching consecutive chars as one match of specific length.
Comparing a reference-string with a hypothesis leads to several match-Lengths and one "NoMatchChars"-value: the count of unmatching chars of both: reference and hypothesis.
A TextAffinity-Object stores these informations.
Several hypotheses compared with the same reference lead to several TextAffinity-Objects, and the challenge is to order them by significance.
This is, how two TextAffinities compare:

1. Loop matchLengths from big to small and compare - terminate at first occurence of a difference - the bigger wins.
2. If one TextAffinity runs out of matchLengths - the other wins.
3. If both are run out at same iteration, then the smaller NoMatchChars wins.

Optimizations:
We can simply append the negative NoMatchChars to the MatchLengths. Then 3) is dispensable, since it is done within the steps before.
Note: The algorithm 1) + 2) is nothing but what in Maths is known as "Lexicographical order" ( <- please follow the link )
And moreover: There already is a high-performance lexicographic-compare-Method in the Framework : static string.CompareOrdinal(x, y).
So the challenge now is to convert our concatenized MatchLengths and NoMatchChars to a string - while respecting the negative signed value of NoMatchChars.
Its not that complicated: An Offset solves the signed-value-Problem, and Convert-class can convert char <-> int:

/// <summary> implements IComparable&lt;TextAffinity&gt; - to be used as Sortkey </summary>
public class TextAffinity : IComparable<TextAffinity> {

   private readonly string _SortKey;       // MatchLengths and negative count of no-matching-chars, all encoded whithin a string

   private const int _Offs = 32767; // offset enables numb-char-conversion for negative numbs too.
   private static int Char2Numb(char c) { return Convert.ToInt32(c) - _Offs; }
   private static char Numb2Char(int n) { return Convert.ToChar(_Offs + n); }

   public TextAffinity(IEnumerable<int> orderedMatchLengths, int noMachChars) {
      var numbs = orderedMatchLengths.Concat(new int[] { -noMachChars }).ToArray();     // append reciprocal noMatchChars
      if (noMachChars > _Offs) throw new ArgumentException("must <= " + _Offs, "noMachChars");
      if (numbs.Any(n => n > _Offs)) throw new ArgumentException("all of them must <= " + _Offs, "orderedMatchLengths");
      _SortKey = new string(numbs.Select(Numb2Char).ToArray());      // convert to String
   }
   public int CompareTo(TextAffinity other) { return string.CompareOrdinal(_SortKey, other._SortKey); }
   
   public override string ToString() { return string.Join(" ", _SortKey.Select(Char2Numb)); }
}

Note: The chars of _SortKey are not readable - propably no Font on earth can display them in a meaningful manner. But it is a sortable string.
And since TextAffinity implements IComparable<TextAffinity>, it can easily be used for sorting:

// string reference, string[] hypotheses
var afffac = new TextAffinityFactory(reference);
var rankedHypotheses = from h in hypotheses orderby afffac.GetAffinity(h) descending select h;

(That was the simple part, yet.)

Figure Out All Matches

Given as reference: " daring end " and as hypothesis: " dark sprints end "

First, I tried a naive, permutative way: Build all possible char-groups of both, and look, which matches on which. The result was fine - but the performance ... ... ... - ähm - not fine.

But another night I remembered, how Levenshtein computes its results: Namely using a matrix, where the columns represent the hypothesis, and the rows represent the reference.
Within such a matrix I mark up matchings of rows and columns:

It's eye-catching, that matching char-groups appear as descending diagonals. I presumed also to enter the length of the found matches.

Note, the match-char ' ' at position ( 0 / 0 ) is not connected with positions ( 1 / 1 ) - (3 / 3 ).
That anomalies rule is, that ' ' only joins a match, if the other end of the match also is a ' '. This crude-rule increases word-match-lengths with 2 points, which leads to a strong preference of word-matches over other char-match-groups.
Look: Because ' end ' matches as full-word, it counts as 5, while 'dar' only counts 3.

Again, I created a small class, this time, to store Match-Information, namely the Match-Start (X / Y) and its Length:

private class Match : IComparable<Match> {
   public int Y, X;
   public int Length = 1;
   public Match(int y, int x) { this.Y = y; this.X = x; }

   /// <summary> defines order by Length descending </summary>
   public int CompareTo(Match other) { return other.Length - Length; }
}

It also is IComparable, since - according to the TextAffinity-Definition - sortation by MatchLength is crucial.

See the loops to fill my matrix:

  1  Match[,] matchMatrix = new Match[yLength, xLength];
  2  for (var x = 0; x < xLength; x++) if (xChars[x] == ' ') AddNewMatch(0, x);  // init top row
  3  for (var y = 0; y < yLength; y++) if (yChars[y] == ' ') AddNewMatch(y, 0);    // init left column
  4  for (int y = 1; y < yLength; y++) {                            // inner matrix
  5     var cy = yChars[y];
  6     for (int x = 1; x < xLength; x++) {
  7        if (xChars[x] == cy) {
  8           var mtPrev = matchMatrix[y - 1, x - 1];
  9           if (mtPrev==null) AddNewMatch(y, x); 
 10           else {    // lengthen mtPrev
 11              mtPrev.Length += 1;
 12              matchMatrix[y, x] = mtPrev;
 13           }
 14        }
 15     }
 16  }

You see: my matchMatrix is not a simple int-Matrix, but is a Matrix of Matches!
And when a char-match occurs at a position x/y - line#7 - then I try to get the previous match from the top-left cell-neighbor, lengthen it, and assign it to the current cell too.
This mirrors, what I've done above, when I entered the Match-Lengths into the grid.
Otherwise - no prev-Match detected - the AddNewMatch() - Method creates a new Match, assigns it to the Matrix as well as to a Match-List (not shown here).
Next I will sort that Match-list, examine its entries and do wired things with them.

Eliminate Overlapping Matches

The figure above shows all possible matches, but some of them are in conflict with others. Eg the 'r' in row#3 cannot match to column#3 and column#8 too!
Again rule simple - code tricky. The rule: Prefer the longer matches; start with them.
Let's try clarify that with colors:

Can you see it? I went from longest to shortest diagonal, and threw their horizontal and vertical "toxic shadow", where other matches can't subsist.
Only 4 matches of different length remain - their ordered matchLengths are: (5 3 2 1)

Then remind the "word-preference-anomalie", which prevents spaces from joining matches, which are no words. Without this anomalie, the match-char at position ( 0 / 0 ) would connect, and we would get overall matchLengths of (5 4 2).
Now - instead of the given " dark sprints end " imagine another hypothesis: " Spring enemy ".
On given reference: " daring end ", but without word-preference-rule, " Spring enemy " would contain the matching char-group "ring en", and would  lead (including the enclosing spaces) to (7 1 1) - which would win highly over (5 4 2) - (" dark sprints end ").
But humans see " dark sprints end " as more similar to " daring end " than " Spring enemy " - right?

So keep stuck with the word-anomalie, which lets " dark sprints end "(5 3 2 1) win over " Spring enemy "(4 2 1 1 1)

But first the Overlap-Eliminating Code:

  1  int[] yMatchMask = new int[yLength];
  2  int[] xMatchMask = new int[xLength];
  3  matches.Sort();
  4  for (var id = 0; id <= matches.Count - 1; id++) {
  5     var match = matches[id];
  6     for (var i = 0; i <= match.Length - 1; i++) {
  7        var y = match.Y + i;
  8        var x = match.X + i;
  9        if (yMatchMask[y] == 0 && xMatchMask[x] == 0) {    // both matchMasks must be free at y/x 
 10           yMatchMask[y] = id + 1;
 11           xMatchMask[x] = id + 1;
 12        }
 13     }
 14  }

For y- and x-direction, I create an int-Array as kind of "mask".
Then, loop the descending sorted matches (mentioned above) and enter the match-id at position.X into the xMask, and at position.Y into the yMask - but only if both masks are not already occupied at that positions.
Since longer matches proceed first, shorter ones get kicked off.

derive noMatchChars and matchLengths from xMatchMask

For example: 4 2 2 2 0 0 0 0 0 3 3 0 0 1 1 1 1 1 is the resulting xMatchMask, from the reference/hypothesis-sample as shown in the Grid-Images.
Note that the ids-values are ordered descending by match-length, while the positions mirrors the match-positions on the Matrix-Columns.

  1  var matchIds = xMatchMask.Where(id => id > 0).ToArray();
  2  var noMatchChars = xLength + yLength - matchIds.Length * 2;  // NoMatchChars sums x-Nomatches and y-Nomatches
  3  var matchLengths = from grp in matchIds.GroupBy(i => i) let length = grp.Count() where length > 1 orderby length descending select length;
  4  return new TextAffinity(matchLengths, noMatchChars);

1. First select the matchIds from the matchMask
2. Then calculate noMatchChars
3. matchLengths are the lengths of the groups of matchIds, if containing more than one element
4. pass these informations to TextAffinity-Ctor - we have already seen, how there is built a Sortkey-string for best compare-performance.

Word-preference-anomalie - Code-Reprise

Sorry, in the "Figure out all matches" - section, I gave a very simplified code - without the annoying anomalie.
Now here it goes how it really goes - whole story:

  1  /// <summary> the evaluated Affinity is IComparable - u can use it in orderby-Sortations </summary>
  2  public TextAffinity GetAffinity(string hypothesis) {
  3     var xChars = MakeCharArray(hypothesis);
  4     var yChars = Chars;
  5     var yLength = yChars.Length;
  6     var xLength = xChars.Length;
  7     Match[,] matchMatrix = new Match[yLength, xLength];
  8     List<Match> matches = new List<Match>();
  9     Action<int, int> AddNewMatch = (y, x) => {
 10        var mt = new Match(y, x);
 11        matches.Add(mt);
 12        matchMatrix[y, x] = mt;
 13     };
 14     Action<Match> CutWordStartFromMatch = mt => {
 15        for (var i = mt.Length; i-- > 0; ) if (xChars[mt.X + i] == ' ') {
 16              if (++i == mt.Length) return; // i is the index after ' '
 17              //cut is done by inserting a new, shorter match (and update all dependant data)
 18              var mt2 = new Match(mt.Y + i, mt.X + i) { Length = mt.Length - i };
 19              matches.Add(mt2);
 20              mt.Length = i;
 21              for (i = mt2.Length; i-- > 0; ) matchMatrix[mt2.Y + i, mt2.X + i] = mt2;
 22              return;
 23           }
 24     };
 25  // mark the matrix:
 26     for (var x = 0; x < xLength; x++) if (xChars[x] == ' ') AddNewMatch(0, x);  // init top row
 27     for (var y = 0; y < yLength; y++) if (yChars[y] == ' ') AddNewMatch(y, 0);  // init left column
 28     for (int y = 1; y < yLength; y++) {                            // inner matrix
 29        var cy = yChars[y];
 30        for (int x = 1; x < xLength; x++) {
 31           var mtPrev = matchMatrix[y - 1, x - 1];
 32           if (xChars[x] == cy) {
 33              if (mtPrev.Null() || (cy == ' ' && xChars[mtPrev.X] != ' ')) {
 34                 AddNewMatch(y, x); // AddNewMatch either on no mtPrev or on invalid word
 35              }
 36              else {    // lengthen mtPrev
 37                 mtPrev.Length += 1;
 38                 matchMatrix[y, x] = mtPrev;
 39              }
 40           }
 41           else {  // on Un-Match mtPrev cannot be a word-Match. check, 
 42                   // whether there a beginning ' ' is to cut off
 43              if (mtPrev.NotNull() && mtPrev.Length > 1 && 
 44              xChars[mtPrev.X] == ' ') CutWordStartFromMatch(mtPrev);
 45           }
 46        }
 47     }
 48  // create matchMasks:
 49     int[] yMatchMask = new int[yLength];
 50     int[] xMatchMask = new int[xLength];
 51     matches.Sort();
 52     for (var id = 0; id <= matches.Count - 1; id++) {
 53        var match = matches[id];
 54        for (var i = 0; i <= match.Length - 1; i++) {
 55           var y = match.Y + i;
 56           var x = match.X + i;
 57           if (yMatchMask[y] == 0 && xMatchMask[x] == 0) { // both matchMasks must be free at y/x 
 58              yMatchMask[y] = id + 1;
 59              xMatchMask[x] = id + 1;
 60           }
 61        }
 62     }
 63     return new TextAffinity(xMatchMask, yLength);
 64  }

First, try understand #33 ff: Although there may be a matching ' ', and may be a previous match mtPrev: Don't append ' ' to mtPrev, if mtPrev doesn't start with ' '.

Now note the anonymous method CutWordStartFromMatch() in line#14.
Then look at line#41 - detecting UnMatches.
If so, check, whether there is a previous match and if it starts with a ' ' this would violate the word-preference-anomalie (since currently an Unmatch occurred). If so - repair that by calling CutWordStartFromMatch().

Conclusion

I'm unsure whether it was a good idea to dive such deep into the micro-granulated algorithm-mud.

Since the very most important point of this article is, just to introduce my new Concept of textual similarity, with its much better results than the common known levenshtein-algorithm,

Ok - Match-Detecting by performant Matrix-Operations probably also is a nice-to-know.

And the "match-masking-trick" to eliminate overlapping matches may be nice too.

And converting int[] to string is definitely funny - isn't it?

But the word-anomalie-stuff - brrr!

Hard to explain, taking much article-space, claiming much brain-power and a stubborn will to understand - from you, the audience - I'm sorry for that.

One more note: The TextAffinity-Approach is about 40% faster than Levenshtein - as implemented in the attached sources. My tests showed, that sorting the data is not the time-consumer, but filling the matrix is.
And while Levenshtein enters complex "cost-evaluation-results" into each Matrix-Cell, TextAffinity mostly just reads. Only on char-match-occurence TextAffinity enters something into the Cell.